1 Introdução
O minério de ferro e as terras raras contêm átomos ou íons que possuem momentos magnéticos permanentes (L T Baczewski 1993). As propriedades magnéticas dos materiais magnéticos são causadas pelo spin e movimento orbital dos elétrons. Visto que lidamos com partículas subatômicas, há necessidade da teoria quântica do momento angular para se determinar o momento magnético de materiais magnéticos. Para recordar pontos importantes, sugiro a leitura destes artigos. Vamos falar hoje sobre o momento magnético e aprender a determinar seu valor através dos números quânticos de spin (S), de momento angular orbital (L) e de momento angular total (J).
2 Momento magnético
A figura 2.1 mostra L (o momento angular orbital), S (o spin), J (o momento angular total), μ/γL (o momento magnético dividido pela razão giromagnética) e μJ/γL (uma componente do momento magnético, porém, na direção do momento angular total).
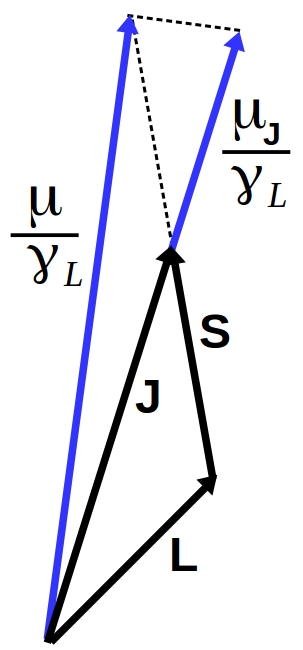
Figura 2.1: O momento total é a soma do momento orbital com o momento de spin. O momento magnético não dispara paralelo ao momento total.
Os operadores vetoriais da figura acima se relacionam da seguinte maneira:
J=L+S.
μγL=L+2S.
μJγL=gJ.
O módulo do momento angular total é:
|J|=ℏ√J(J+1).
Por isso, o módulo de (2.3) é:
|μJγL|=gℏ√J(J+1).
Na equação acima, reconhecendo que |γL|ℏ=μB (magneton de Bohr), obtém-se:
|μJ|μB=g√J(J+1).
E a expressão do fator de Landé depende dos números quânticos S, L e J:
g=32+S(S+1)−L(L+1)2J(J+1).
A próxima seção mostrará como determinar esses números quânticos. Assim, poderemos determinar o fator de Landé (2.7) e o momento magnético (2.6).
3 Determinação do momento magnético
Em um átomo, um elétron fica acomodado em uma camada (n), em uma subcamada (n,l) e em um orbital (n,l,ml). Os possíveis valores desses números quânticos são:
n=1,2,3,4,…l=0,1,2,3,…,n−1ml=l,l−1,…,−l+1,−l
Acrescente o fato do elétron possuir spin (s) com projeção–z (ms):
s=12ms=±12
Isso quer dizer que são permitidos dois elétrons em cada órbita (n,l,ml,ms).
Há uma convensão de chamar os valores de l por letras:
l=0 → sl=1 → pl=2 → dl=3 → f⋮
As subcamadas comportam um número limitado de elétrons. Por exemplo, a subcamada 3d possui 5 orbitais: ml=2,1,0,−1,−2. Se cada orbital aceita dois elétrons com spins opostos, então, essa subcamada pode acomodar até 10 elétrons — escreve-se 3d10. A subcamada 4f pode acomodar até 14 elétrons (3d14), isso porque contém 7 orbitais: ml=3,2,1,0,−1,−2,−3.
Os átomos dos materiais magnéticos do grupo do ferro (Sc–Cu) e do grupo das terras raras (Ce–Lu) possuem muitos elétrons, suas subcamadas, 3d e 4f, respectivamente, ficam parcialmente preenchidas. Para lidar com essa situação, Russell e Saunders (H N Russell 1925) consideraram que os momentos orbitais dos elétrons se combinam para resultar em um momento orbital atômico, o mesmo acontecendo com os spins dos elétrons, que se combinam para resultar em um spin atômico:
L=∑lS=∑s
Ademais, L e S também se combinam (2.1) para resultar em um momento angular total atômico, J. As somas (3.4) implicam que as componentes z dos momentos orbitais e dos spins dos elétrons também se combinam:
ML=∑mlMS=∑ms
O procedimento (3.5) pode ser realizado nas subcamadas de um átomo. É fácil mostrar que as subcamadas preenchidas por completo resultam em somas iguais a zero. Devemos, então, analisar as subcamadas incompletas. A figura 3.1 mostra como efeturar essas somas usando como exemplo as subcamadas 3d2 e 3d7. As duas subcamadas não estão preenchidas por completo, porém, há uma diferença marcante: a subcamada 3d2 está menos da metade cheia e a subcamada 3d7 está mais da metade cheia. Isso afeta a maneira de se determinar o momento angular total. De acordo com uma regra de Hund:
O momento angular total é J=|L−S| quando a subcamada está menos da metade cheia, e J=L+S quando a subcamada está metade ou mais da metade cheia.
Outra regra de Hund diz que os elétrons tendem a ocupar orbitais diferentes para reduzir sua repulsão eletrostática e que o valor de L é:
L=max{ML}.
Por isso, os dois elétrons da subcamada 3d2 não escolhem os orbitais ml=1,0 (ML=1), resolvem, sim, se estabelecerem nos osbitais ml=2,1 (ML=3).
E mais outra regra de Hund diz que os spins dos elétrons em orbitais diferentes são paralelos e que o valor de S é:
S=max{MS}.
Por isso, os dois elétrons da subcamada 3d2 não são os com spins ms=12,−12 (MS=0), mas, sim, são os com spins ms=12,12 (MS=1).
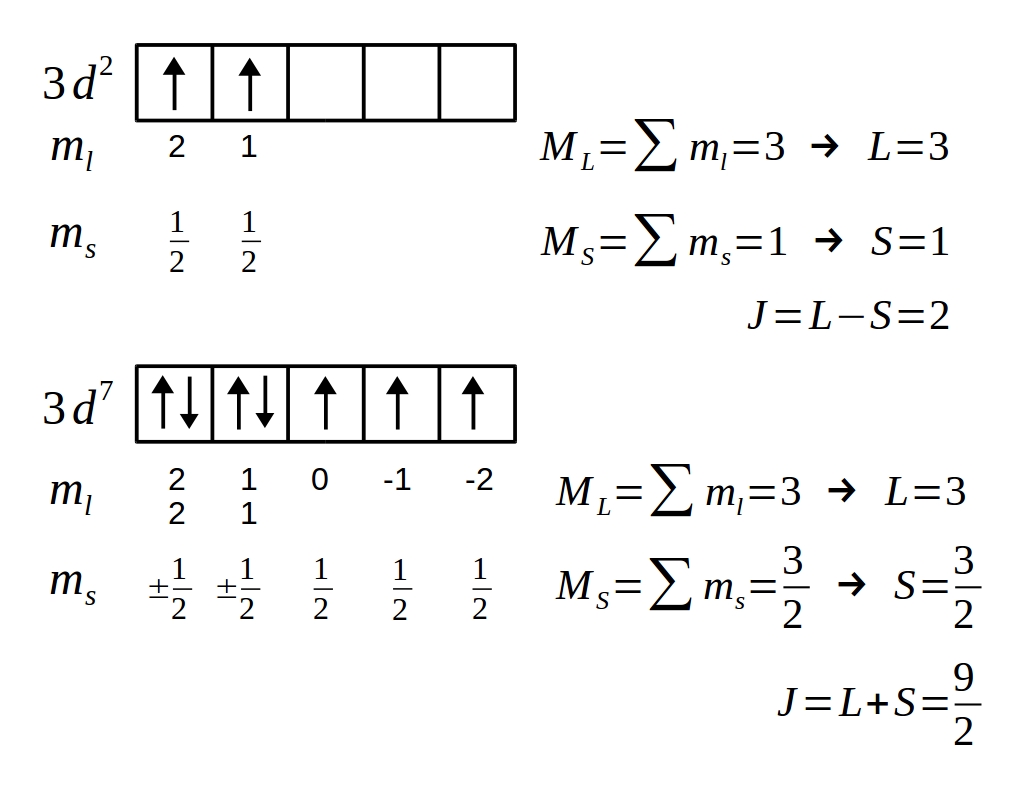
Figura 3.1: Determinação dos números quânticos L, S e J para as subcamadas 3d2 e 3d7.
Tendo em mãos os valores de S, L e J —veja novamente a figura 3.1—, o fator de Landé (2.7) é assim determinado:
3d2→g=32+(1)(1+1)−(3)(3+1)2(2)(2+1)=0.6673d7→g=32+(32)(32+1)−(3)(3+1)2(92)(92+1)=1.333
Por fim, determina-se o momento magnético do átomo no estado fundamental (2.6):
3d2→|μJ|μB=(0.667)√(2)(2+1)⟹|μJ|=1.63μB3d7→|μJ|μB=(1.333)√(92)(92+1)⟹|μJ|=6.63μB
E, como foi dito, os valores (3.9) se referem ao momento magnético na direção de J, conforme ilustrado na figura 2.1.
4 Conclusão
Você pode usar o procedimento da figura 3.1 para determina o momento magnético da série 3d1 até 3d10; também da série 4f1 até 4f14. Olhando uma tabela periódica, principalmente no bloco dos metais de transição (grupo do ferro: Sc–Cu) e no do bloco dos lantanídeos (grupo das terras raras: Ce–Lu), você vai conserguir identificar os elementos dessas séries. Por exemplo, a configuração eletrônica do Co (cobalto) é: [Ar]3d74s2. Isso quer dizer que o íon Co2+ tem configuração: [Ar]3d7.