1 Introdução
Oscilador harmônico na picture de Heisenberg resolve o oscilador harmônico na formulação de Heisenberg (I J R Aitchison 2004). Para tal, utiliza a equação de movimento:
dGdt=∂G∂t+[G,H]iℏ.
Geralmente, o tempo não é explícito na fórmula de G e a derivada parcial desse operador é zero. Daí, a equação (1.1) se torna mais simples:
˙G=[G,H]iℏ.
No artigo acima, trabalhamos com o hamiltoniano que descreve o movimento unidimensional de uma partícula de massa m submetida por uma força restauradora:
H=12mp2+m2ω2q2.
Agora, vamos trabalhar com o hamiltoniano de Caldirola–Kanai (Caldirola 1941) , (Kanai 1948), que incorpora, ao hamiltoniano (1.3), o efeito de uma força de atrito através de um parâmetro de fricção γ:
H=e−γt12mp2+e+γtm2ω2q2.
2 Modelo CK
O modemo de Caldirola–Kanai, conhecido como modelo CK, trata da dissipação de energia em sistemas quânticos. Utilizando a equação de movimento (1.2) e o hamiltoniano (1.4), vamos determinar a evolução temporal do operador de coordenada, q(t), e a evolução temporal do operador de momento linear, p(t), de um oscilador harmônico que dissipa energia para um meio ambiente viscoso, caracterizado pelo parâmetro de fricção γ. O meio γ pode ser um gás de fundo que cerca o oscilador; e o oscilador pode ser um átomo aprisionado nesse meio; então, a cada oscilação, o átomo dissipar energia para o gás de fundo. Nosso primeiro passo é desenvolver o comutador coordenada–hamiltoniano:
[q,H]=[q,12mp2e−γt]+[q,m2ω2q2e+γt]=12me−γt[q,p2]+m2ω2e+γt[q,q2]=12me−γt2p[q,p]+0=e−γtmpiℏ,
que gera a equação de movimento da coordenada:
˙q=[q,H]iℏ=e−γtmp.
Nessas e em outras passagens matemáticas é importante lembrar:
A condição quântica entre os operadores de coordenada e de momento linear:
[q,p]=iℏ[p,q]=−iℏ[q,q]=[p,p]=0
E estas comutações:
[a,bc]=[a,b]c+b[a,c][a,b2]=2b[a,b]
Nosso segundo passso é desenvolver o comutador momento–hamiltoniano:
[p,H]=[p,12mp2e−γt]+[p,m2ω2q2e+γt]=12me−γt[p,p2]+m2ω2e+γt[p,q2]=0+m2ω2e+γt2q[p,q]=−mω2e+γtqiℏ,
que gera a equação de movimento do momento:
˙p=[p,H]iℏ=−mω2e+γtq.
Equação diferencial da coordenada:
Vamos inverter a equação (2.2):
p=e+γtm˙q.
Derivar a equação (2.2):
¨q=e−γtm(−γp+˙p).
E substituir p (2.7) e ˙p (2.6) em ¨q (2.8):
¨q=e−γtm(−γe+γtm˙q−mω2e+γtq)=−γ˙q−ω2q.
O que resulta em:
¨q+γ˙q+ω2q=0.
Equação diferencial do momento:
Agora vamos inverter a equação (2.6):
q=−e−γtmω2˙p.
Derivar da equação (2.6):
¨p=−mω2e+γt(γq+˙q).
E substituir q (2.11) e ˙q (2.2) em ¨p (2.12):
¨p=−mω2e+γt(−γe−γtmω2˙p+e−γtmp)=γ˙p−ω2p.
O que resulta em:
¨p−γ˙p+ω2p=0.
As equações (2.10) e (2.14) são resolvidas com a técnica de reescrever essas equações com variáveis complexas (escritas com letras maiúsculas):
¨Q+γ˙Q+ω2Q=0,¨P−γ˙P+ω2P=0.
Daí, fazer toda matemática usando as variáveis complexas — o que torna a nossa vida mais fácil! No final das contas, as soluções físicas são obtidas tomando a parte real (ou a parte imaginária) de cada solução complexa:
q=Re(Q) ou Im(Q),p=Re(P) ou Im(P).
Uma solução simples para a equação da coordenada:
A solução que vamos escolher para a coordenada complexa será do tipo Q=eRt. Fazendo ˙Q e ¨Q, e substituindo em (2.15), obtém-se:
R2+γR+ω2=0.
A solução dessa tradicional equação de segundo grau é:
R=−γ±√γ2−4ω22.
Ou:
R=−γ2±√γ24−ω2.
Visto que a procura é por oscilação subamortecida (γ2/4<ω2), em que a fricção não neutraliza o movimento bruscamente, invertemos a raiz (2.19) para o resultado ser negativo:
R=−γ2±i√ω2−γ24.
Agora podemos chamar:
¯ω=√ω2−γ24,
e escrever:
R=−γ2±i¯ω.
O resultado (2.22) mostra que a solução complexa é o produto destas exponenciais:
Q=e−γ2te±i¯ωt,
o que implica na seguinte solução física:
q=e−γ2t Re(e±¯ωt).
Portanto, a evolução temporal do operador de coordenada é:
q(t)=e−γ2tcos(¯ωt).
O efeito da fricção γ afeta a oscilação, pois, o oscilador abandona a sua frequência natural ω, e passa a oscilar com a frequência reduzida ¯ω; além da amplitude de oscilação diminuir exponencialmente.
Uma solução simples para a equação do momento:
A solução complexa será do tipo P=eGt. Substituindo em (2.15), obtém-se:
G2−γG+ω2=0,
cuja solução é:
G=+γ2±√γ24−ω2.
Para oscilação subamortecida:
G=+γ2±i¯ω,
com:
¯ω=√ω2−γ24.
Então, a solução complexa é:
G=e+γ2te±i¯ωt.
A parte real de (2.30) repete a solução cosseno da coordenada (ver quadro anterior). Portanto, a solução física do momento será:
p=e+γ2t Im(e±¯ωt),
ou:
p=e+γ2t(±sin(¯ωt)).
Visto que o momento é a derivada da posição, e a posição é do tipo cosseno, dentre as 2 soluções acima, é conveniente escolher a negativa. Portanto, a evolução temporal do operador de momento linear é:
p(t)=e+γ2t(−sin(¯ωt)).
As Figs. 2.1, 2.2 e 2.3 foram construídas para γ=0.2. Houve simplificações numéricas: ajustou-se m=1 e ω=1. Isso implicou em ¯ω=0.995. Apresenta-se o comportamento dos seguintes operadores de Heisenberg: coordenada, momento linear, energia potencial, energia cinética e energia total.

Figura 2.1: Oscilação da coordenada (vermelho). Fator de amortecimento = 0.2.

Figura 2.2: Oscilação do momento (verde). Fator de amortecimento = 0.2.

Figura 2.3: Oscilação da energia potencial (vermelho) e da energia cinética (verde). A energia total permanece constante (azul). Fator de amortecimento = 0.2.
A Fig. 2.1 está de acordo com o que pensamos sobre um sistema dissipativo. Durante a oscilação, a amplitude da coordenada diminui de valor (tende a zero). Porém, a figura 2.2 mostra que a amplitude do momento está aumentando. E a figura 2.3 deixa claro que a energia total não está se dissipando: se apresenta como uma constante de movimento.
o modelo FALHA em explicar um sistema quântico dissipativo.
O mesmo comportamento foi observado por (Segovia-Chaves 2018): FIGURE 2. Foi dito que isso se deve ao aumento exponencial da massa do oscilador de Caldirola-Kanai. De fato, podemos entender o que foi dito, fazendo um ajuste no hamiltoniano (1.4) (S K Bose 1985):
H(t)=12me+γtp2(t)+me+γt2ω2q2(t).
A chamar:
m(t)=me+γt,
obtém-se:
H(t)=12m(t)p2(t)+m(t)2ω2q2(t).
O hamiltoniano (2.36) é analogo ao hamiltoniano do oscilador harmônico sem atrito (1.3), porém, com uma massa que cresce exponencialmente com o passar do tempo. Nessa interpretação, o oscilador fica mais “pesado” a cada oscilação.
3 Modelo CK com duas fricções
O modelo dissipativo de Caldirola–Kanai, da Seção 2, gera estes operadores de coordenada e de momento:
q(t)=e−γ2tcos(¯ωt),p(t)=e+γ2t(−sin(¯ωt)).
O que tornou esse modelo falho, foi o momento crescer por causa do termo e+γ2t. Se a exponencial fosse decrescente, como na coordenada, o modelo seria dissipativo e a energia total diminuiria com o tempo. Visando “reparar as coisas,” pensei em alterar o hamiltoniano (1.4). A minha ideia é analisar o modelo CK, porém, com duas fricções:
H(t)=e−aγt12mp2+e+bγtm2ω2q2.
As constantes a e b são números reais. O estudo segue o procedimento e a linguagem da Seção 2. Nosso primeiro passo é desenvolver o comutador coordenada–hamiltoniano:
[q,H]=[q,12mp2e−aγt]+[q,m2ω2q2e+bγt]=12me−aγt[q,p2]+m2ω2e+bγt[q,q2]=12me−aγt2p[q,p]+0=e−aγtmpiℏ,
que gera a equação de movimento da coordenada:
˙q=[q,H]iℏ=e−aγtmp.
Nosso segundo passso é desenvolver o comutador momento–hamiltoniano:
[p,H]=[p,12mp2e−aγt]+[p,m2ω2q2e+bγt]=12me−aγt[p,p2]+m2ω2e+bγt[p,q2]=0+m2ω2e+bγt2q[p,q]=−mω2e+bγtqiℏ,
que gera a equação de movimento do momento:
˙p=[p,H]iℏ=−mω2qe+bγt.
Equação diferencial da coordenada:
Inverter a equação (3.4):
p=m˙qe+aγt.
Derivar a equação (3.4):
¨q=e−aγtm(−aγp+˙p).
Substituir p (3.7) e ˙p (3.6) em ¨q (3.8):
¨q=e−aγtm(−aγm˙qe+aγt−mω2qe+bγt)=−aγ˙q−ω2e(b−a)γtq.
O que resulta em:
¨q+aγ˙q+ω2e(b−a)γtq=0.
Uma solução simples para a equação da coordenada:
Usar esta coordenada complexa, Q=eRt, em (3.10):
R2+aγR+ω2e(b−a)γt=0.
Solução:
R=−aγ±√(aγ)2−4ω2e(b−a)γt2.
Ou:
R=−aγ2±√a2γ24−ω2e(b−a)γt.
Visto que a procura é por oscilação subamortecida, invertemos a raiz (3.13) para o resultado ser negativo:
R=−aγ2±i√ω2e(b−a)γt−a2γ24.
Vamos chamar:
Ωa=√ω2e(b−a)γt−a2γ24,
para escrever (3.14) como:
R=−aγ2±iΩa.
Em fim, a coordenada complexa é:
Q=e−aγ2te±iΩat,
e a coordenada física é:
q=e−aγ2t Re(e±Ωat),
ou:
q(t)=e−aγ2tcos(Ωat).
Equação diferencial do momento:
Inverter a equação (3.6):
q=−e−bγtmω2˙p.
Derivar a equação (3.6):
¨p=−mω2e+bγt(bγq+˙q).
Substituir q (3.20) e ˙q (3.4) na equação ¨p (3.21):
¨p=−mω2e+bγt(−bγe−bγtmω2˙p+e−aγtmp)=bγ˙p−ω2e(b−a)γtp.
O que resulta em:
¨p−bγ˙p+ω2e(b−a)p=0.
Uma solução simples para a equação do momento:
Usar este momento complexo, P=eGt, em (3.23):
G2−bγG+ω2e(b−a)γt=0.
Solução:
G=+bγ2±√b2γ24−ω2e(b−a)γt.
Inverter a raiz de (3.25) e chamar o resultado de:
Ωb=√ω2e(b−a)γt−b2γ24.
Assim:
G=+bγ2±iΩb,
e o momento complexo é:
P=e+bγ2te±iΩbt.
Por fim, acompanhando a escolha na Seção 2, a solução física do momento é:
p(t)=e+bγ2t(−sin(Ωbt)).
É prátivo escrever um resumo com os operadores de coordenada e de momento:
q(t)=cos(Ωat)e−aγ2t,p(t)=−sin(Ωbt)ebγ2t,
e com as frequêcias de oscilações:
Ωa=√ω2e(b−a)γt−(aγ)24,Ωb=√ω2e(b−a)γt−(bγ)24.
Analisando essas frequências, se a=b=1, as fórmulas (3.31) regridem para (2.21): Ωa=Ωb=¯ω. As outras situações são:
b>ab<a⟹e(b−a)γt→∞e(b−a)γt→0⟹Ω→∞Ω→NaN
Nota:
NaN (Not a Number) é uma palavra da linguagem R.
Em (3.32), avisa que o usuário tentou obter a raiz quadrada de um número negativo.
3.1 Exemplo 1
Os gráficos 3.1, 3.2 e 3.3 são construídos para a=1, b=−1 e γ=0.2. Ajustou-se a frequência natural em ω=1. A coordenada e o momento (3.30) e as frequêcias (3.31) são:
q(t)=cos(Ωat)e−γ2t,p(t)=−sin(Ωbt)e−γ2t,
Ωa=√e−2γt−γ24,Ωb=√e−2γt−γ24,
sendo que essas frequências se tornam NaN após 11.5 s.
O hamiltoniano (3.2), para m=1, tem o aspécto:
H(t)=12p2e−γt+12q2e−γt.
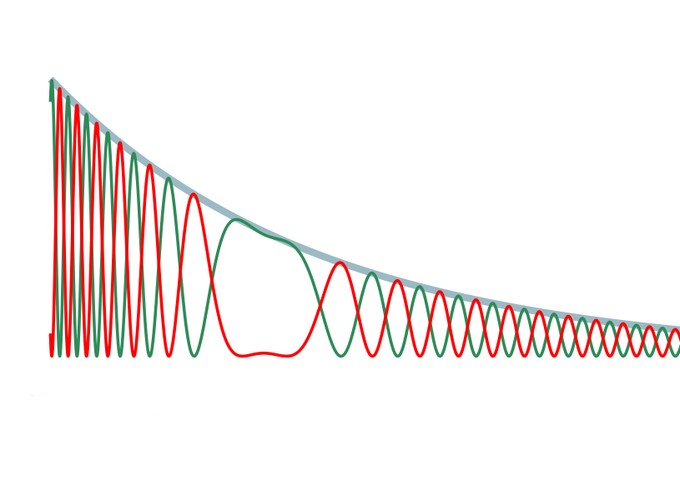
As frequências de oscilação diminuem com o tempo de acordo com a figura 3.1. Com a possibilidade de manipular duas fricções no hamiltoniano CK, a figura 3.2 mostra que a amplitude da coordenada e a amplitude do momento tendem a zero. Como consequência, a figura 3.3 mostra que as amplitudes das energias cinética e potencial também tendem a zero, e, principalmente, o operador de energia total diminui com o tempo (não é uma constante de movimento). Esse comportamento está de acordo com o que pensamos sobre um modelo dissipativo: a cada oscilação, o oscilador perde energia para um meio ambiente viscoso. Como dissemos, o meio pode ser um gás de fundo que cerca o oscilador; o oscilador pode ser um átomo aprisionado nesse meio. Agora, a dissipação é causada por duas fontes de viscosidades, modeladas pelas fricções aγ e bγ. Nesse modelo de dupla viscosidade, o movimento vê uma viscosidade e a força restauradora, outra.

Figura 3.1: a = 1, b = -1 e gamma = 0.2: frequência da coordenada (vermelho); frequência do momento (verde).

Figura 3.2: a = 1, b = -1 e gamma = 0.2: oscilação da coordenada (vermelho); oscilação do momento (verde).

Figura 3.3: a = 1, b = -1 e gamma = 0.2: oscilação da energia potencial (vermelho); oscilação da energia cinética (verde); há dissipação de energia total (azul).
Nesse exemplo, o oscilador foi cercado por um fundo áspero: (a,b)=(1,−1). Isso permitiu pouca oscilação (11.5 s). Os próximos exemplos vão “suavizar as coisas.”
3.2 Exemplo 2
Os gráficos 3.4, 3.5 e 3.6 são construídos para (a,b)=(0.1,−0.1) e γ=0.2. As frequências se tornam NaN após 230 s (~4 minutos). Segue a lista de equações graficadas.
Coordenada e momento (3.30):
q(t)=cos(Ωat)e−0.01t,p(t)=−sin(Ωbt)e−0.01t.
Frequências (3.31):
Ωa=√e−0.04t−10−4,Ωb=√e−0.04t−10−4.
Hamiltoniano (3.2):
H(t)=12p2e−0.02t+12q2e−0.02t.

Figura 3.4: a = 0.1, b = -0.1 e gamma = 0.2: frequência da coordenada (vermelho); frequência do momento (verde).

Figura 3.5: a = 0.1, b = -0.1 e gamma = 0.2: oscilação da coordenada (vermelho); oscilação do momento (verde).

Figura 3.6: a = 0.1, b = -0.1 e gamma = 0.2: oscilação da energia potencial (vermelho); oscilação da energia cinética (verde); há dissipação de energia total (azul).
Há dissipação de energia e, como diminuímos a fricção, o oscilador oscilou por muito mais tempo (comparado com o Exemplo 1). Existem algumas marcações nas figuras que serão explicadas no próximo exemplo.
3.3 Exemplo 3
Os gráficos 3.7, 3.8 e 3.9 são construídos para (a,b)=(0.01,−0.01) e γ=0.2. As frequências se tornam NaN após 3450 s (~1 hora). Segue a lista de equações graficadas.
Coordenada e momento (3.30):
q(t)=cos(Ωat)e−0.001t,p(t)=−sin(Ωbt)e−0.001t.
Frequências (3.31):
Ωa=√e−0.004t−10−6,Ωb=√e−0.004t−10−6.
Hamiltoniano (3.2):
H(t)=12p2e−0.002t+12q2e−0.002t.
Nesse exemplo, quando o tempo passa pelo intervalo [475-500] segundos, centrado em 500 s, o oscilador não completa um ciclo total (extremidade–extremidade), faz a inversão em meio-ciclo (extremidade–posição de equilíbro). As outras oscilações ocorrem normalmente: invertem os movimentos nas extremidades dos percursos. Porém, a inversão atípica é feita ao redor da posição de equilíbrio: q=0. O retorno pelas extremidades é realizada “num piscar de olhos.” Já a situação atípica necessita de mais tempo: 50 s. Durante esse intervalo, o momento linear estabiliza ao redor do máximo, p=−0.6, quer dizer, o oscilador faz o retorno em posição de alta velocidade. O comportamento incomum é refletido no gráfico das energias. Durante os 50 segundos, a energia potencial se localiza em V=0, e a energia cinética entre K=0.06 e 0.075. Depois da oscilação atípica, o oscilador volta a oscilar normalmente, através das extremidades do percursor.

Figura 3.7: a = 0.01, b = -0.01 e gamma = 0.2: frequência da coordenada (vermelho); frequência do momento (verde).

Figura 3.8: a = 0.01, b = -0.01 e gamma = 0.2: oscilação da coordenada (vermelho); oscilação do momento (verde).

Figura 3.9: a = 0.01, b = -0.01 e gamma = 0.2: oscilação da energia potencial (vermelho); oscilação da energia cinética (verde); há dissipação de energia total (azul).
Voltando ao Exemplo 2, observa-se no gráfico 3.5 que o oscilador também realiza uma oscilação incomum por volta dos 50 segundos: faz um retorno antes de chegar na extremidade do percurso; por isso, realiza essa inversão com velocidade diferente de zero. Em inversões típicas, a velocidade na extremidade do percurso é zero: ver a marcação logo após 100 s.
4 Conclusão
A dissipação de energia por sistemas quânticos é um problema de grande complexidade. Os autores (Chung-In Um 2002), em um resumo com cerca de 130 páginas, fazem um “levantamento cronológico das várias abordagens para os osciladores harmônicos amortecidos linearmente, desde o ano de 1931 até meados da década de 1980.” Um problema apontado é que muitos desses modelos, incluindo o modelo Caldirola–Kanai (CK), violam o principal fundamento da física quântica: o princípio de incerteza de Heisenberg.
De acordo com o trabalho de (Segovia-Chaves 2018), ao utilizar o modelo CK, também observamos falhas na descrição do oscilador que dissipa energia para um meio viscoso — recorde as figuras 2.2 e 2.3. Foi, então, sugerido a utilização de 2 parâmetros de fricção: um para o movimento e outro para a força restauradora — recorde o hamiltoniano (3.2). Os exemplos nas seções 3.2 e 3.3 mostram que essa proposta gera oscilações atípicas, hora o retorno da oscilação ocorre antes de chegar na extremidade do percurso, hora, pela posição de equilíbrio — recorde as figuras 3.5 e 3.8, respectivamente.