1 Introdução

Há duas meneiras de decrever a interação da radiação eletromagnética com a matéria (átomos). A versão semi–clássica considera o campo como ondas eletromagnéticas clássicas (de energia contínua) e os átomos como sistemas quânticos (com energia discreta e função de onda). Na versão quântica, os átomos são quantizados, e, também, o campo é quantizado (na forma de um conjunto de osciladores quânticos): Isso cria duas situações distintas: a excitação do campo é descrita por fótons que possuem energia proporcional à frequência \((n\hbar\omega)\) e a ausência de fótons \((n=0)\) manifesta a energia de ponto zero, ou energia de vácuo \((\frac{1}{2}\hbar\omega)\).

Quando o campo é tratado quanticamente, fenômenos que antes não eram descritos pelo campo clássico, passam a ser explicados. O exemplo mais famoso é o fenômeno da emissão espontânea — idealizada por Einstein (Einstein 1917). Ao utilizar o campo clássico, a emissão espontânea é explicada de maneira indireta, através dos coeficientes de Einstein. Porém, ao utilizar o campo elétrico como um operador quântico de campo elétrico, a taxa de emissão espontânea é resultado (natural) da aplicação da regra da transição atômica, mais conhecida como regra de ouro de Fermi (Stedman 1971) (J M Zhang 2016).

Neste artigo, vamos deduzir a regra de ouro de Fermi e usá-la para determinar as taxas de absorção e emissão de fótons decorrentes do acoplamento fóton–átomo.

2 Regra de ouro para perturbação periódica

Vamos determinar a probabilidade e a taxa de transição para um sistema com dois níveis de energia (por exemplo, um átomo ou um poço quântico). As transições possíveis são do nível \(1\) para o nível \(2\) (absorção) e do nível \(2\) para o nível \(1\) (emissão). O sistema é “banhado” por um campo elétrico que oscila periodicamente, com frequência angular \(\omega\) (por exemplo, pelo campo elétrico da radiação visível: 400 – 750 THz).

Há um elétron em órbita ao redor do núcleo do sistema. Sua posição é \(\vec{r}\) e sua carga é \(e=-q\), sendo \(q = 1.602 \times 10^{-19}\ {\rm C}\). O efeito da distribuição dessa carga ao redor do núcleo será considerado análogo ao efeito de um dipolo elétrico, de vetor:

\[\begin{equation} \vec{D} = e\vec{r} = -q\vec{r} . \tag{2.1} \end{equation}\]

A interação do elétron–dipolo com o campo elétrico produz esta energia (o sinal de menos faz parte da fórmula):

\[\begin{equation} h = -\vec{E} \cdot \vec{D} . \tag{2.2} \end{equation}\]

O campo elétrico aponta na direção do vetor de polarização \(\vec{\Lambda}\):

\[\begin{equation} \vec{E}(\vec{r},t) = \vec{\Lambda} \mathscr{E}(\vec{r}) \mathscr{e}^{-i\omega t} . \tag{2.3} \end{equation}\]

Isso implica em:

\[\begin{equation} h(t) = q (\vec{\Lambda} \cdot \vec{r}) \mathscr{E}(\vec{r}) \mathscr{e}^{-i\omega t} . \tag{2.4} \end{equation}\]

Agora, chamando:

\[\begin{equation} h _ 0 = q (\vec{\Lambda} \cdot \vec{r}) \mathscr{E}(\vec{r}) , \tag{2.5} \end{equation}\]

a perturbação periódica é:

\[\begin{equation} h(t) = h _ 0 \mathscr{e}^{-i\omega t} . \tag{2.6} \end{equation}\]

A probabilidade de transição é estudada no artigo Comportamento dependente do tempo da probabilidade de transição. A considerar um sistema com dois níveis de energia, no regime de acoplamento fraco, a amplitude de probabilidade de transição, do estado fundamental para o estado excitado, é determinada resolvendo:

\[\begin{equation} \frac{d C _ {2 \gets 1}}{dt} = \frac{1}{i \hbar} \langle \varphi _ {2} |h(t)| \varphi _ {1} \rangle \mathscr{e}^{i (E _ {2} - E _ {1}) t / \hbar} . \tag{2.7} \end{equation}\]

A substituir a perturbação periódica:

\[\begin{equation} \frac{d C _ {2 \gets 1}}{dt} = \frac{1}{i \hbar} \langle \varphi _ {2} |h_0 e^{-i\omega t}| \varphi _ {1} \rangle \mathscr{e}^{i (E _ {2} - E _ {1}) t / \hbar} . \tag{2.8} \end{equation}\]

O que implica em:

\[\begin{equation} \frac{d C _ {2 \gets 1}}{dt} = \frac{1}{i \hbar} \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t / \hbar} . \tag{2.9} \end{equation}\]

Se a perturbação começa em \(t=0\), a solução dessa equação é:

\[\begin{equation} C _ {2 \gets 1} = \frac{1}{i \hbar} \int_0^t dt' \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t' / \hbar} . \tag{2.10} \end{equation}\]

Ou:

\[\begin{equation} C _ {2 \gets 1} = \frac{1}{i \hbar} \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle \int_0^t dt' \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t' / \hbar} . \tag{2.11} \end{equation}\]

Agora, resolve-se a integral:

\[\begin{equation} \small \begin{aligned} C _ {2 \gets 1} &= \frac{1}{i \hbar} \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle \int_0^t dt' \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t' / \hbar} \\ &= \frac{1}{i \hbar} \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle \frac{1}{i (E _ {2} - E _ {1} - \hbar\omega) / \hbar} \left( \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t / \hbar} -1 \right) \\ &= - \frac{\langle \varphi _ {2} |h_0| \varphi _ {1} \rangle}{E _ {2} - E _ {1} - \hbar\omega} \left( \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t / \hbar} -1 \right) \times \frac{2i \mathscr{e}^{-i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar}} {2i \mathscr{e}^{-i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar}} \\ &= - \frac{\langle \varphi _ {2} |h_0| \varphi _ {1} \rangle}{E _ {2} - E _ {1} - \hbar\omega} \left( \frac{ \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar} - \mathscr{e}^{-i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar} }{2i} \right) \times \frac{2i}{\mathscr{e}^{-i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar}} \\ &= - \frac{\langle \varphi _ {2} |h_0| \varphi _ {1} \rangle}{E _ {2} - E _ {1} - \hbar\omega} \times \sin \Big[ (E _ {2} - E _ {1} - \hbar\omega) \tfrac{t}{2\hbar} \Big] \times 2i \times \mathscr{e}^{i (E _ {2} - E _ {1} - \hbar\omega) t / 2\hbar} . \end{aligned} \tag{2.12} \end{equation}\]

Essa amplitude de probabilidade resulta na probabilidade de transição:

\[\begin{equation} | C _ {2 \gets 1} |^2 = | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 \times 4 \frac{\sin^2 \Big[ (E _ {2} - E _ {1} - \hbar\omega) \frac{t}{2\hbar} \Big]} {(E _ {2} - E _ {1} - \hbar\omega)^2} . \tag{2.13} \end{equation}\]

Esse resultado pode ser melhorado. A multiplicar por \(\frac{t}{2\hbar}\):

\[\begin{equation} | C _ {2 \gets 1} |^2 = | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 \times 4 \frac{\frac{t}{2\hbar} \sin^2 \Big[ (E _ {2} - E _ {1} - \hbar\omega) \frac{t}{2\hbar} \Big]} {(E _ {2} - E _ {1} - \hbar\omega)^2 \frac{t}{2\hbar} } , \tag{2.14} \end{equation}\]

obtém-se:

\[\begin{equation} | C _ {2 \gets 1} |^2 = \frac{2t}{\hbar} | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 \times \frac{\sin^2 \Big[ (E _ {2} - E _ {1} - \hbar\omega) \frac{t}{2\hbar} \Big]} {(E _ {2} - E _ {1} - \hbar\omega)^2 \frac{t}{2\hbar} } . \tag{2.15} \end{equation}\]

A substituir o delta, a probabilidade de transição causada pela perturbação periódica é:

\[\begin{equation} | C _ {2 \gets 1} |^2 = \frac{2\pi t}{\hbar} | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 \delta(E _ {2} - E _ {1} - \hbar\omega) . \tag{2.18} \end{equation}\]

A taxa de transição \((W)\) é a probabilidade de transição por unidade de tempo. É determinada fazendo a derivada da probabilidade de transição no tempo. Isso nos leva à regra de ouro de Fermi para o caso de perturbação periódica e transição do estado fundamental para o excitado:

A taxa de transição para a absorção depende do delta. Isso significa que transições por segundo ocorrerão se a radiação estimuladora for monocromática, com frequência \((\omega)\) igual à frequência da transição atômica \((E_{2} - E_{1})/\hbar\). A “força da transição” está no termo:

\[\begin{equation} \begin{aligned} | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 &= | \langle \varphi _ {2} | q (\vec{\Lambda} \cdot \vec{r}) \mathscr{E}(\vec{r}) | \varphi _ {1} \rangle |^2 \\ &= q^2 | \langle \varphi _ {2} | (\vec{\Lambda} \cdot \vec{r}) | \varphi _ {1} \rangle |^2 | \langle \varphi _ {2} | \mathscr{E}(\vec{r}) | \varphi _ {1} \rangle |^2 . \end{aligned} \tag{2.20} \end{equation}\]

Pode-se chamar de \(\theta\), o ângulo entre o vetor de polarização do campo elétrico e vetor de posição do elétron. Nesse caso,

\[\begin{equation} | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 = q^2 \cos^2\theta | \langle \varphi _ {2} | \vec{r} | \varphi _ {1} \rangle |^2 | \langle \varphi _ {2} | \mathscr{E}(\vec{r}) | \varphi _ {1} \rangle |^2 . \tag{2.21} \end{equation}\]

Ademais, pode-se levar em conta todos ângulos entre o vetor de polarização e o vetor posição, substituindo a média \(\overline{\cos^2 \! \theta}=\frac{1}{3}\):

\[\begin{equation} | \langle \varphi _ {2} |h_0| \varphi _ {1} \rangle |^2 = \tfrac{1}{3} q^2 | \langle \varphi _ {2} | \vec{r} | \varphi _ {1} \rangle |^2 | \langle \varphi _ {2} | \mathscr{E}(\vec{r}) | \varphi _ {1} \rangle |^2 . \tag{2.22} \end{equation}\]

A taxa de emissão também é determinada através dos passos (2.7) até (2.19) — com algumas adaptações:

\(\rm (a)\) A equação da amplitude de probabilidade para a transição do estado excitado para o fundamental é:

\[\begin{equation} \frac{d C _ {1 \gets 2}}{dt} = \frac{1}{i\hbar} \langle \varphi _ {1} |h(t)| \varphi _ {2} \rangle e^{i (E _ {1} - E _ {2}) t / \hbar} . \tag{2.23} \end{equation}\]

\(\rm (b)\) A perturbação (2.6) é substituída por:

\[\begin{equation} h(t) = h _ 0 \mathscr{e}^{+i\omega t} . \tag{2.24} \end{equation}\]

\(\rm (c)\) O resultado é:

Figura 2.1: Contorno da função pico de difração.

3 Campo como osciladores quânticos

Ideias quânticas para o campo eletromagnético apresenta consequências do campo eletromagnético oscilar como oscilam osciladores quânticos. Nessa representação, a energia armazenada no campo é quantizada em fótons (deixa de ser contínua). Também, a energia não parte do zero, há energia, na ausência de fótons, a chamada energia de vácuo de fótons ou energia do ponto zero. Robert Bennett et al apresentam outro ponto importante: A quantização do campo eletromagnético se dá pela transforção do campo elétrico em um operador de campo elétrico e pela trasformação do campo magnético em um operador de campo magnético. O operador de campo elétrico e o operador de campo magnético são escritos em termos de operadores do oscilador quântico: do operador de criação de excitação própria \((a^{+})\) e do operador de aniquilação de excitação própria \((a)\); e o hamiltoniano do campo eletromagnético se torna análogo ao hamiltoniano de um conjunto independente de osciladores quânticos.

O acoplamento do campo elétrico espacial com o dipolo elétrico se manifesta nesta expressão:

\[\begin{equation} h _ 0 = -\vec{\mathscr{E}}(\vec{r}) \cdot \vec{D} . \tag{3.1} \end{equation}\]

Nota: O termo temporal \(\mathscr{e}^{-i\omega t}\) foi parar dentro da fórmula da regra de ouro — veja a passagem (2.8) \(\to\) (2.9).

O dipolo é criado pelo elétron (carga negativa):

\[\begin{equation} \vec{D} = e \vec{r} = -q \vec{r} . \tag{3.2} \end{equation}\]

A substituir (3.2) em (3.1):

\[\begin{equation} h _ 0 = q \vec{\mathscr{E}}(\vec{r}) \cdot \vec{r} . \tag{3.3} \end{equation}\]

A forma quantizada do campo elétrico é (Robert Bennett 2016):

\[\begin{equation} \vec{\mathscr{E}}(\vec{r}) = i \vec{\Lambda} \sqrt{\frac{\hbar \omega}{2\varepsilon _ {0} L^3}} \left( a e^{i\vec{k}\cdot\vec{r}} - a^{+} e^{-i\vec{k}\cdot\vec{r}} \right) . \tag{3.4} \end{equation}\]

Essa fórmula pode ser simplificada para o caso de ondas no visível. Por exemplo, a luz vermelha (400 THz) possui magnitude de vetor de onda igual a \(k = 8.4 \times 10^{6}\) \(\rm m^{-1}\). Se o raio da orbita do elétron for considerado igual ao raio de Bohr \((r = a_0 = 0.53 \times 10^{10}\) \(\rm m)\), obtém-se, \(kr = 0.00045 \ll 1\) e \(e^{\pm i\vec{k}\cdot\vec{r}} \approx 1\), o que implica em:

\[\begin{equation} \vec{\mathscr{E}}(\vec{r}) = i \vec{\Lambda} \sqrt{\frac{\hbar \omega}{2\varepsilon _ {0} L^3}} \left( a - a^{+} \right) . \tag{3.5} \end{equation}\]

Na equação acima, \(\vec{\Lambda}\) é o vetor de polarização.

O estado número de fóton \((|n\rangle)\) representa \(n\) fótons de energia \(\hbar\omega\). Os operadores aniquilação \((a)\) e criação \((a^{+})\) operam da seguinte maneira nesse estado:

\[\begin{equation} \begin{aligned} a |n\rangle &= \sqrt{n} |n-1\rangle ,\\ a^{+} |n\rangle &= \sqrt{n+1} |n+1\rangle . \end{aligned} \tag{3.6} \end{equation}\]

A substituir (3.5) em (3.3):

\[\begin{equation} h _ 0 = iq (\vec{\Lambda} \cdot \vec{r}) \sqrt{\frac{\hbar \omega}{2\varepsilon _ {0} L^3}} \left( a - a^{+} \right) . \tag{3.7} \end{equation}\]

Pela simplicidade, vamos considerar a onda se propagando na direção do eixo \(z\), \(\vec{k} = k \hat{z}\), e o campo elétrico polarizado verticalmente (na direção do eixo \(x\)), \(\vec{\Lambda} = \hat{x}\), conforme ilustrado na Fig. 3.1. Visto que o vetor que posiciona o elétron dentro do átomo tem coordenadas \(\vec{r}=x\hat{x}+y\hat{y}+z\hat{z}\), obtém-se:

\[\begin{equation} \begin{aligned} \vec{k} \cdot \vec{r} &= kz ,\\ \vec{\Lambda} \cdot \vec{r} &= x ,\\ h _ 0 &= iqx \sqrt{\frac{\hbar \omega}{2\varepsilon _ {0} L^3}} \left( a - a^{+} \right) . \end{aligned} \tag{3.8} \end{equation}\]

A tornar a notação mais clara, vamos escrever:

\[\begin{equation} h _ 0 = S \left( xa - xa^{+} \right) , \tag{3.9} \end{equation}\]

e chamar:

\[\begin{equation} \begin{aligned} S &= iq \sqrt{\frac{\hbar \omega}{2\varepsilon _ {0} L^3}} ,\\ |S|^2 &= q^2 \frac{\hbar \omega}{2\varepsilon _ {0} L^3} . \end{aligned} \tag{3.10} \end{equation}\]

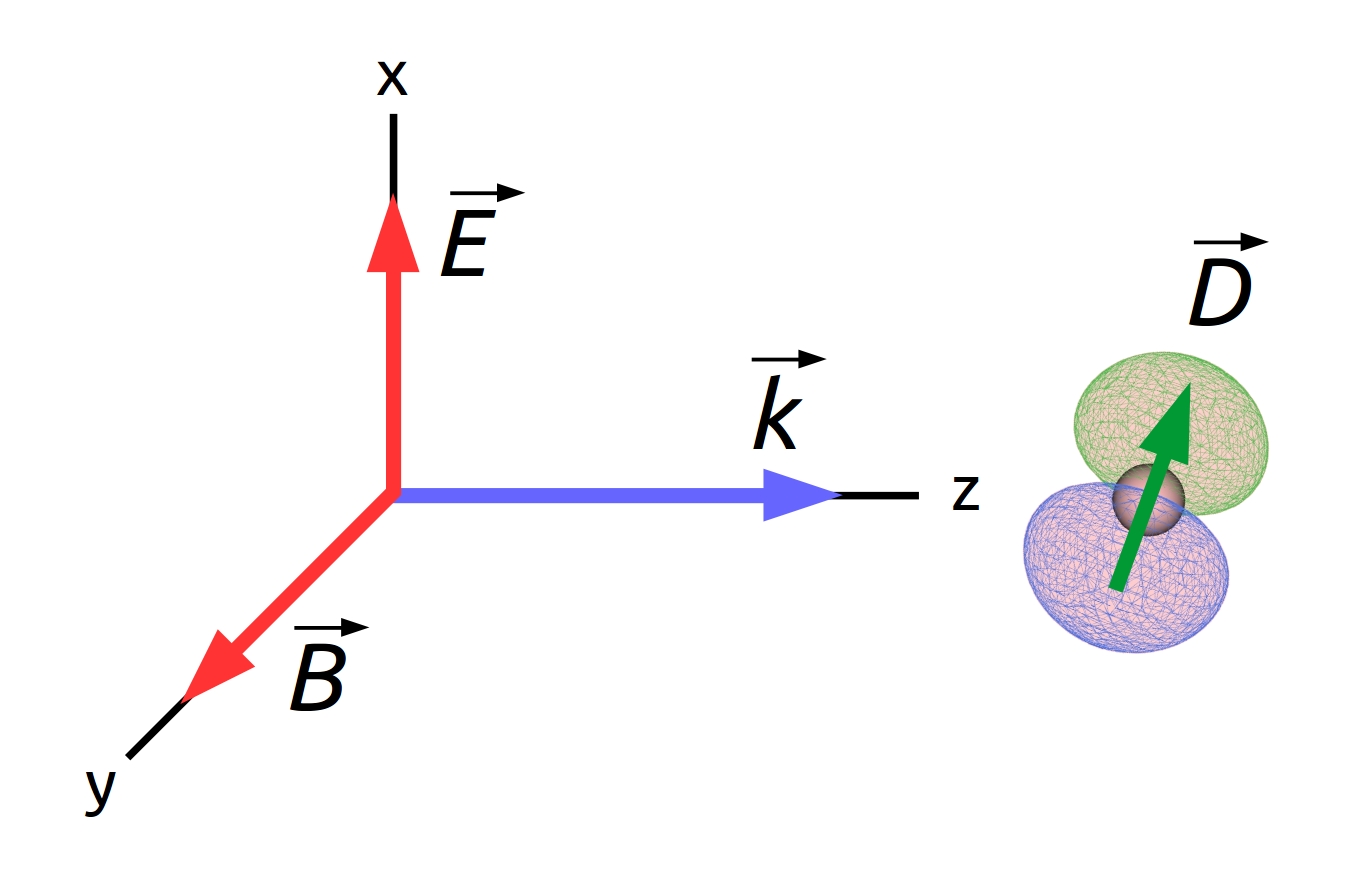
Figura 3.1: Vista esquemática de um campo elétrico polarizado verticalmente se propagando para interagir com um dipolo elétrico com orientação arbitrária.

4 Taxa de absorção

Vamos trabalhar com a regra de ouro preparada para o caso da absorção (2.19) e com a equação (3.9).

O átomo (ou o poço quântico) se encontra no estado fundamental \((\phi _ {1})\). Ao seu redor, há \((n)\) fótons. O átomo sofre transição para o estado excitado \((\phi _ {2})\) : absorve um fóton. Agora, ao seu redor há \((n-1)\) fótons.

Antes da transição, o sistema átomo/fótons estava no estado:

\[\begin{equation} |\varphi _ {1} \rangle = |\phi _ {1} \rangle |n \rangle = |\phi _ {1}, n \rangle . \tag{4.1} \end{equation}\]

Depois da transição, o sistema foi para o estado:

\[\begin{equation} |\varphi _ {2} \rangle = |\phi _ {2} \rangle |n-1 \rangle = |\phi _ {2}, n-1 \rangle . \tag{4.2} \end{equation}\]

A substituir os estados na equação (2.19), obtém-se

\[\begin{equation} W _ {2 \gets 1} = \frac{2\pi}{\hbar} | \langle \phi _ {2}, n-1 |h_0| \phi _ {1}, n \rangle |^2 \delta(E _ {2} - E _ {1} - \hbar\omega) . \tag{4.3} \end{equation}\]

A utilizar as propriedades dos operadores:

\[\begin{equation} \begin{aligned} \langle \phi _ {2}, n-1 |xa| \phi _ {1}, n \rangle &= \langle \phi _ {2} |x| \phi _ {1} \rangle \langle n-1 |a| n \rangle = \langle \phi _ {2} |x| \phi _ {1} \rangle \sqrt{n} ,\\ \langle \phi _ {2}, n-1 |xa^{+}| \phi _ {1}, n \rangle &= \langle \phi _ {2} |x| \phi _ {1} \rangle \langle n-1 |a^{+}| n \rangle = 0 . \end{aligned} \tag{4.4} \end{equation}\]

E a substituir os resultados acima na equação (4.3):

\[\begin{equation} W _ {2 \gets 1} ^{\rm absorção} = n \frac{2\pi}{\hbar} |S|^2 | \langle \phi _ {2} |x| \phi _ {1} \rangle |^2 \delta(E _ {2} - E _ {1} - \hbar\omega) . \tag{4.5} \end{equation}\]

5 Taxa de emissão

Agora vamos trabalhar com a regra de ouro preparada para o caso da emissão (2.25) e novamente com a equação (3.9).

O átomo (ou o poço quântico) se encontra no estado excitado \((\phi _ {2})\). Ao seu redor, há \((n)\) fótons. O átomo sofre transição para o estado fundamental \((\phi _ {1})\): emite um fóton. Agora, ao seu redor há \((n+1)\) fótons.

Antes da transição, o sistema átomo/fótons estava no estado:

\[\begin{equation} |\varphi _ {2} \rangle = |\phi _ {2} \rangle |n \rangle = |\phi _ {2}, n \rangle . \tag{5.1} \end{equation}\]

Depois da transição, o sistema foi para o estado:

\[\begin{equation} |\varphi _ {1} \rangle = |\phi _ {1} \rangle |n+1 \rangle = |\phi _ {1}, n+1 \rangle . \tag{5.2} \end{equation}\]

A substituir os estados na equação (2.25), obtém-se

\[\begin{equation} W _ {1 \gets 2} = \frac{2\pi}{\hbar} | \langle \phi _ {1}, n+1 |h_0| \phi _ {2}, n \rangle |^2 \delta(E _ {1} - E _ {2} + \hbar\omega) . \tag{5.3} \end{equation}\]

A utilizar as propriedades dos operadores:

\[\begin{equation} \begin{aligned} \langle \phi _ {1}, n+1 |xa| \phi _ {2}, n \rangle &= \langle \phi _ {1} |x| \phi _ {2} \rangle \langle n+1 |a| n \rangle = 0 ,\\ \langle \phi _ {1}, n+1 |xa^{+}| \phi _ {2}, n \rangle &= \langle \phi _ {1} |x| \phi _ {2} \rangle \langle n+1 |a^{+}| n \rangle = \langle \phi _ {1} |x| \phi _ {2} \rangle \sqrt{n+1} . \end{aligned} \tag{5.4} \end{equation}\]

E a substituir os resultados acima na equação (5.3):

\[\begin{equation} W _ {1 \gets 2} = (n+1) \frac{2\pi}{\hbar} |S|^2 | \langle \phi _ {1} |x| \phi _ {2} \rangle |^2 \delta(E _ {1} - E _ {2} + \hbar\omega) . \tag{5.5} \end{equation}\]

Essa equação pode ser separada em duas partes:

\[\begin{equation} W _ {1 \gets 2} ^{\rm estimulada} = n \times \frac{2\pi}{\hbar} |S|^2 | \langle \phi _ {1} |x| \phi _ {2} \rangle |^2 \delta(E _ {1} - E _ {2} + \hbar\omega) . \tag{5.6} \end{equation}\]

\[\begin{equation} W _ {1 \gets 2} ^{\rm espontânea} = 1 \times \frac{2\pi}{\hbar} |S|^2 | \langle \phi _ {1} |x| \phi _ {2} \rangle |^2 \delta(E _ {1} - E _ {2} + \hbar\omega) . \tag{5.7} \end{equation}\]

O método foi capaz de explicitar a taxa de transição da emissão espontânea! Algo não realizável considerando o campo elétrico na sua forma clássica. O conceito de emissão espontânea é fruto da mente brilhante de Einstein (Einstein 1917). Todavia, seu trabalho não considerou o campo de acordo com a teoria eletromagnética quântica. A quantização do campo eletromagnético foi realizada pela primeira vez por Dirac (Dirac 1927). O resultado (5.7) prova que a emissão espontânea decorre da quantização do campo eletromagnético.

A emissão espontânea não depende dos fótons que rodeiam o átomo: observe que o número de fótons \((n)\) só pararece na fórmula da emissão estimulada. Isso significa que qualquer corpo (mesmo na ausência de fótons) emite radiação espontânea — o que se conclui:

A emissão espontânea é estimulada pelo campo de vácuo.

Os resultados (5.6) e (5.7) mostram que os fótons podem ser produzidos por emissão estimulada ou espontânea. Uma vez gerados por emissão espontânea, esses fótons podem ser utilizados para impulsionar a emissão estimulada — princípio básico do funcionamento de um laser: a emissão espontânea dá o “pontapé inicial” na contagem do número de fótons necessário para desencadear a emissão estimulada — e amplificar o número de fótons emitidos.

6 Modos de campo eletromagnético

A decomposição do campo eletromagnético em componentes dinamicamente independentes é chamada de decomposição de modo normal. Um análogo geométrico seria a decomposição de um vetor em suas componentes ao longo dos eixos \((x,y,z)\). A decomposição de modo normal é mais “robusta” que a vetorial, pois envolve mais elementos. Por exemplo, um conjunto infinito de ondas transversais planas é o caso mais famoso de uma base de modos normais utilizada para realizar decomposição.

Um campo elétrico genérico \(\left(\vec{E}\right)\), então, pode ser decomposto em modos normais independentes \(\left(\vec{E}_\ell\right)\), sendo cada \(\ell\) caracterizado por quatro números \(\big(n_x,n_y,n_z,\Lambda\big)\):

\[\begin{equation} \vec{E} (\vec{r},t) = \sum _ \ell \vec{E} _ \ell (\vec{r},t) . \tag{6.1} \end{equation}\]

Somar em \(\ell\) significa correr os quatro índices. Os três primeiros \((n_x,n_y,n_z)\) são números inteiros (positivos, negativos ou zero) e estão relacionados com o vetor de propagação (o número de onda é quantizado dentro de uma caixa cúbica de volume \(\rm L_{box}^3\)):

\[\begin{equation} \vec{k} = k _ x\hat{x} + k _ y\hat{y} + k _ z\hat{z} = \frac{2\pi}{\rm L _ {box}} (n _ x\hat{x} + n _ y\hat{y} + n _ z\hat{z}) . \tag{6.2} \end{equation}\]

O contador \(\Lambda\) é decorrente da condição transversal a qual permite 2 polarizações para cada vetor de onda: \(\Lambda=1\), realiza a contagem da polarização \(\vec{\Lambda}_1\); e \(\Lambda=2\), a contagem da polarização \(\vec{\Lambda}_2\).

Entende-se, então, que o contador \(\ell\) pode assumir os seguintes valores:

\[\begin{equation} \begin{aligned} \ell &= \Big( +|n _ x| ,\ +|n _ y| ,\ +|n _ z| ,\ 1 \Big) \\ \ell &= \Big( +|n _ x| ,\ +|n _ y| ,\ +|n _ z| ,\ 2 \Big) \\ \ell &= \Big( -|n _ x| ,\ -|n _ y| ,\ -|n _ z| ,\ 1 \Big) \\ \ell &= \Big( -|n _ x| ,\ -|n _ y| ,\ -|n _ z| ,\ 2 \Big) \end{aligned} \tag{6.3} \end{equation}\]

Nota: É óbivio, se o objetivo é contar vetores de onda (desconsiderando as polarizações), \(\ell\) perde o contador \(\Lambda\), ou seja: \(\ell=(n_x, n_ y, n_z, \Lambda) \to \ell=(n_x, n_ y, n_z)\); e a contagem total cai pela metade:

\[\begin{equation} \begin{aligned} \ell &= \Big( +|n _ x| ,\ +|n _ y| ,\ +|n _ z| \Big) \\ \ell &= \Big( -|n _ x| ,\ -|n _ y| ,\ -|n _ z| \Big) \end{aligned} \tag{6.4} \end{equation}\]

A frequência angular é determinada pela fórmula \(\omega = c\big|\vec{k}\big|\) (e não depende da polarização). Resulta em um mesmo valor quando os vetores de onda apontam em direções opostas: \(\omega_{(\ell>0)} = c\big|\vec{k}_{(\ell>0)}\big| = c\big|\vec{k}_{(\ell<0)}\big| = \omega_{(\ell<0)}\). Isso quer dizer que a onda para a direita e a sua “clone” para a esquerda vibram com a mesma frequência angular. Acrescente a esse quadro as polarizações (duas) e conclua com o auxílio da figura 6.1 que a frequência angular \(\omega_{\ell}\) se relaciona com 4 modos de oscilação.

Modo 1: onda para a direira (polarização vertical).

Modo 2: onda para a direita (polarização horizontal).

Modo 3: onda para a esquerda (polarização vertical).

Modo 4: onda para a esquerda (polarização horizontal).

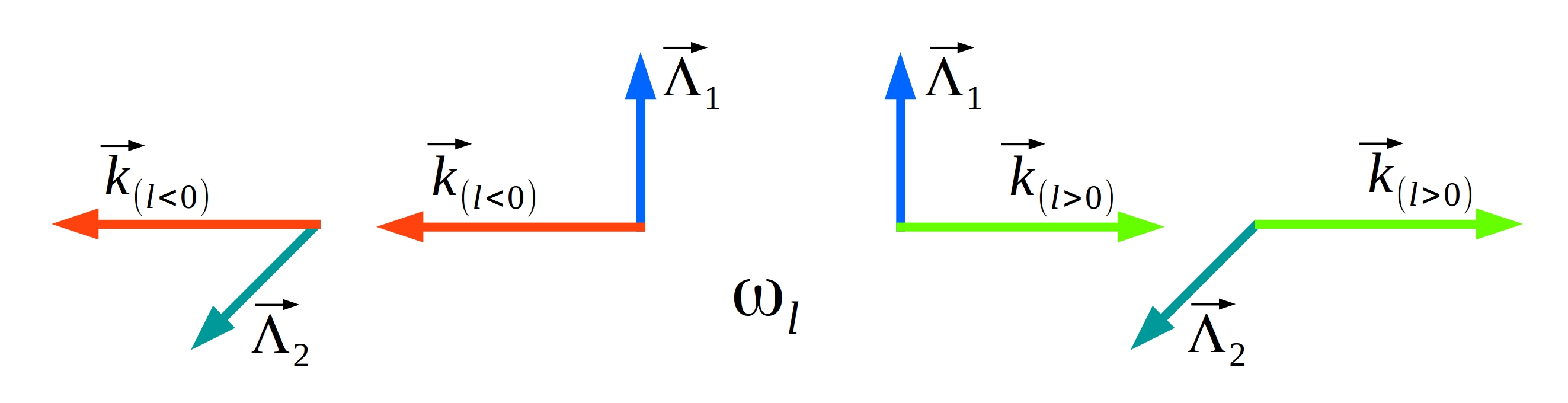
Figura 6.1: Quatro modos do campo eletromagnético que vibram com a mesma frequência angular.

Ao realizar a contagem dos modos esta pergunta deve ser respondida:

Quantos modos existem entre as frequências angulares \(\omega\) e \(\omega + d\omega\)?

Vamos chamar essa resposta de \(g(\omega) d\omega\).

Antes de responder essa questão, devemos nos perguntar:

Quantos vetores de propagação existem entre os números de onda \(k\) e \(k + dk\)?

Vamos chamar essa resposta de \(g(k) dk\). Ao pensar de acordo com a geometria do espaço-k, no eixo \(x\), de acordo com equação (6.2), dois pontos consecutivos, por exemplo, os pontos \(n_x=99\) e \(n_x=100\), estão distantes \(\rm (2\pi / L_{box})\) — análogo para os eixos \(y\) e \(z\). Isso quer dizer, \(\vec{k}\) ocupa o espaço de um cubo de volume \(\rm (2\pi / L_{box})^3\). Em geometria, a fórmula do volume de uma casca esférica é \(4\pi k^2 dk\). Portanto, encontra-se a quantidade de vetores em questão dividindo o volume da casca pelo volume do cubo:

\[\begin{equation} g(k) dk = \frac{4\pi k^2 dk}{\rm (2\pi / L _ {box})^3} = {\rm L _ {box}^3} \frac{k^2}{2\pi^2} dk . \tag{6.5} \end{equation}\]

O resultado acima deve ser corrigido para levar em conta as 2 polarizações transversais dos vetores de propagação:

\[\begin{equation} g(k) dk = 2\times {\rm L _ {box}^3} \frac{k^2}{2\pi^2} dk . \tag{6.6} \end{equation}\]

Nota: A onda plana eletromagnética não polariza ao longo do eixo de propagação. Porém, em sólidos, a onda plana elástica possui 1 modo longitudinal e 2 transversais e a correção se faz \(\times 3\) com o ajuste: \({\rm L _ {box}^3} \to {\rm L _ {solid}^3}\).

O próximo passo é relacionar o número de onda com a frequência angular:

\[\begin{equation} \omega = c\ k \ \ \to \ \ d\omega = c\ dk . \tag{6.7} \end{equation}\]

A substituir os resultados (6.7) no resultado (6.6), obtém-se:

\[\begin{equation} g(\omega) d\omega = {\rm L _ {box}^3} \frac{\omega^2}{\pi^2 c^3} d\omega . \tag{6.8} \end{equation}\]

ou:

\[\begin{equation} g(\omega) = {\rm L _ {box}^3} \frac{\omega^2}{\pi^2 c^3} . \tag{6.9} \end{equation}\]

A dividir por \({\rm L _ {box}^3}\):

\[\begin{equation} \mathtt{g} (\omega) = \frac{\omega^2}{\pi^2 c^3} . \tag{6.10} \end{equation}\]

Unidades e interpretações:

(6.8) \(\rm \Big[ \rm \small adimensional \Big]\): \(g(\omega) d\omega\) é o número de modos entre \(\omega\) e \(\omega + d\omega\).

(6.9) \(\rm \Big[ \frac{1}{s^{-1}} \Big]\): \(g(\omega)\) é o número de modos por unidade de intervalo de frequência angular, ou, a densidade de modos na escala de frequência angular.

(6.10) \(\rm \Big[ \frac{1}{m^3 s^{-1}} \Big]\): \(\mathtt{g} (\omega)\) é o número de modos por unidade de volume por unidade de intervalo de frequência angular.

O gráfico da densidade (6.10) — para alguns valores de frequência comum (Hz) — é apresentado na Fig. 6.2. Observa-se que o canal de alta-frequência disponibiliza mais modos que o de baixa-frequência. Veja, por exemplo, o canal 800 THz disponibiliza \(\rm 100\,000\ modos/m^3/s^{-1}\); enquanto que o canal 400 THz disponibiliza 1/4 desse valor \((\rm 25\,000\ modos/m^3/s^{-1})\).

Figura 6.2: Densidade modos de campo eletromagnético.

Pela simplicidade, agora vamos chamar \({\rm L _ {box}^3}=V\).

Até o momento, a densidade de modos foi escrita na escala de frequência angular. A trabalhar na escala de energia, deve-se lembrar que o número de modos no espaço-energia é igual ao número de modos no espaço-omega:

\[\begin{equation} g(E) dE = g(\omega) d\omega \to g(E) = g( \underbrace{\omega} _ {E\hbar^{-1}} ) \underbrace{\left|\frac{d\omega}{dE}\right|} _ {\hbar^{-1}} . \tag{6.11} \end{equation}\]

E, com a equação (6.9), obtém-se a densidade de modos na escala de energia:

\[\begin{equation} g(E) = V \frac{\left( {E\hbar^{-1}} \right)^2}{\pi^2 c^3} \hbar^{-1} = V \frac{E^2}{\pi^2 c^3 \hbar^3} . \tag{6.12} \end{equation}\]

Outra opção é trabalhar na escala de frequência ordinária. Nesse caso, o número de modos no espaço-frequência é igual ao número de modos no espaço-omega:

\[\begin{equation} g(\nu) d\nu = g(\omega) d\omega \to g(\nu) = g( \underbrace{\omega} _ {2\pi \nu} ) \underbrace{\left|\frac{d\omega}{d\nu}\right|} _ {2\pi} . \tag{6.13} \end{equation}\]

E, novamente com a equação (6.9), obtém-se a densidade de modos na escala de frequência ordinária:

\[\begin{equation} g(\nu) = V \frac{\left( 2\pi \nu \right)^2}{\pi^2 c^3} 2\pi = V \frac{8\pi \nu^2}{c^3} . \tag{6.14} \end{equation}\]

Por fim, se o desejo é trabalhar na escala de comprimento de onda, o número de modos no espaço-lambda é igual ao número de modos no espaço-omega:

\[\begin{equation} g(\lambda) d\lambda = g(\omega) d\omega \to g(\lambda) = g( \underbrace{\omega} _ {c 2\pi \lambda^{-1}} ) \underbrace{\left|\frac{d\omega}{d\lambda}\right|} _ {c 2\pi \lambda^{-2}} . \tag{6.15} \end{equation}\]

E, novamente com a equação (6.9), obtém-se a densidade de modos na escala de comprimento de onda:

\[\begin{equation} g(\lambda) = V \frac{\left( c 2\pi \lambda^{-1} \right)^2}{\pi^2 c^3} c 2\pi \lambda^{-2} = V \frac{8\pi}{\lambda^4} . \tag{6.16} \end{equation}\]

Conexões são importantes. As formas alternativas da energia são:

\[\begin{equation} E = \hbar\omega = h\nu = \frac{hc}{\lambda} . \tag{6.17} \end{equation}\]

Isso quer dizer que:

\(\hspace{5cm} \Large \frac{E}{V}\) \(\times\) (6.9) = \(\Large \frac{\hbar\omega^3}{\pi^2 c^3}\);

\(\hspace{5cm} \Large \frac{E}{V}\) \(\times\) (6.12) = \(\Large \frac{E^3}{\pi^2 c^3 \hbar^3}\);

\(\hspace{5cm} \Large \frac{E}{V}\) \(\times\) (6.14) = \(\Large \frac{8\pi h \nu^3}{c^3}\);

\(\hspace{5cm} \Large \frac{E}{V}\) \(\times\) (6.16) = \(\Large \frac{8\pi hc}{\lambda^5}\).

Agora vem a conexão: Esses termos fazem parte da Lei de Planck quando escrita na escala da frequência angular, energia, frequência ordinária e comprimento de onda, respectivamente — pode-se ver as fórmulas em: Ideias quânticas para o campo eletromagnético.

7 Taxa de transição para um conjunto de estados quase-contínuos

A regra de ouro preparada para os casos de absorção (2.19) e emissão (2.25) se aplica exclusivamente quando o “salto quântico” ocorre entre estados discretos. Mas isso nem sempre acontece! Um dos níveis (fundamantal ou excitado) pode estar centralizado em um conjunto de estados quase-contínuos. Nesse caso, é necessário adaptar as fórmulas — com o auxílio da densidade de estados de elétrons na escala de energia, \(g_{\rm e}(E)\).

Algo que se deve lembrar é a seguinte propriedade da função delta:

\[\begin{equation} \int dx\ f(x) \delta(x - \mathfrak{X}) = f(\mathfrak{X}) . \tag{7.1} \end{equation}\]

Agora vamos trabalhar o caso da absorção e, depois, fazer alguns ajustes para resolver o caso da emissão.

Na absorção, o “salto” é do nível discreto \(E_1\) para um conjunto de níveis quase-contínuos centalizado em \(E_f=E_2\): \(E_a < E_f < E_b\). Isso significa que precisamos somar cada “salto” usando a fórmula (2.19):

\[\begin{equation} W _ {2 \gets 1} = \sum _ {f} \frac{2\pi}{\hbar} | \langle \varphi _ {f} |h_0| \varphi _ {1} \rangle |^2 \delta(E _ {f} - [E _ {1} + \hbar\omega]) . \tag{7.2} \end{equation}\]

Cada termo da equação (7.2) leva em conta a contribuição de “1–salto.” Precisamos somar vários “saltos.” Visto que os níveis de energia são muito próximos uns dos outros, a somatória pode ser substituída por uma integral. O número de “saltos” entre \(E_f\) e \(E_f + dE_f\) é determinado pelo número de estados nesse intervalo: \(g_{\rm e}(E_f) dE_f\). Então, faz-se a troca da \(\sum_{f}\) pela \(\int g_{\rm e}(E_f) dE_f\) (Stedman 1971):

\[\begin{equation} W _ {2 \gets 1} = \frac{2\pi}{\hbar} | \langle \varphi _ {f} |h_0| \varphi _ {1} \rangle |^2 \int dE _ f\ g _ {\rm e}(E _ f) \delta(E _ {f} - [E _ {1} + \hbar\omega]) . \tag{7.3} \end{equation}\]

E, usando a propriedade (7.1):

\[\begin{equation} W _ {2 \gets 1} = \frac{2\pi}{\hbar} | \langle \varphi _ {f} |h_0| \varphi _ {1} \rangle |^2 g _ {\rm e}(E _ {1} + \hbar\omega) . \tag{7.4} \end{equation}\]

Na absorção, \(E_1 + \hbar\omega = E_2\):

O resultado é claro: a taxa de absorção é proporcional à densidade de estados excitados: \(g _ {\rm e}(E _ {2})\).

Você já deve ter concluído que a a taxa de emissão será proporcional à densidade de estados fundamentais: \(g _ {\rm e}(E _ {1})\). Tem razão, na emissão, o “salto” ocorre do nível discreto \(E_2\) para um conjunto de níveis quase-contínuos centalizado em \(E_i=E_1\). A somatória (2.25) se transforma nesta integral:

\[\begin{equation} W _ {1 \gets 2} = \frac{2\pi}{\hbar} | \langle \varphi _ {i} |h_0| \varphi _ {2} \rangle |^2 \int dE _ i\ g _ {\rm e}(E _ i) \delta(E _ {i} - [E _ {2} - \hbar\omega]) . \tag{7.6} \end{equation}\]

E, usando novamente a propriedade (7.1):

\[\begin{equation} W _ {1 \gets 2} = \frac{2\pi}{\hbar} | \langle \varphi _ {i} |h_0| \varphi _ {2} \rangle |^2 g _ {\rm e}(E _ {2} - \hbar\omega) . \tag{7.7} \end{equation}\]

Na emissão, \(E_2 - \hbar\omega = E_1\):

As taxas de transição (7.5) e (7.8) possuem a mesma estrutura. Há uma constante, o termo que expressa a “força da transição” e a densidade de estados de elétrons. Porém, o grande diferencial é o argumento da densidade de estados. Observa-se que a densidade “segue” a seta da transição.

Transição \((2 \gets 1)\) \(\implies\) \(g _ {\rm e}(E _ {2})\) .

Transição \((1 \gets 2)\) \(\implies\) \(g _ {\rm e}(E _ {1})\) .

Conclui-se que a densidade de estados que aparece na regra de ouro de Fermi é a densidade de estados finais.

A fórmula da densidade de estados de elétrons é determinada usando princípios da mecânica quântica atômica. Mas acredito ser possível buscar um caminho alternativo. Vamos raciocinar. Na emissão, cada transição \((i \gets 2)\) gera 1-fóton de energia \((E_2 - E_i)\). As várias transições — para um conjunto de estados quase-contínuos — vão gerar um acúmulo de fótons com energia ao redor de \((E_2 - E_1)\). A equação (6.12) expressa a densidade de modos de campo eletromagnético na escala de energia, a qual, está relacionada com a emissão atômica que está relacionada com a densidade de estados fundamentais. Portanto, a densidade de estados finais que entra na equação (7.8) [e também na (7.5)] pode ser substituída pela densidade de estados de fótons:

\[\begin{equation} g _ {\rm e}(E _ {1}) \to g(E _ {2} - E _ {1}) = V _ {\rm box} \frac{(E _ {2} - E _ {1})^2}{\pi^2 c^3 \hbar^3} . \tag{7.9} \end{equation}\]

Esse resultado é incrível! Mostra que a emissão é controlada pelo volume da caixa! Quer dizer, se fizermos uma caixa bem pequena, da ordem de grandeza do comprimento de onda que o átomo deseja emitir, é possível ocorrer a supressão da emissão atômica (W Jhe 1987).

8 Conclusão

A descrição quântica da interação da radiação eletromagnética com a matéria, em que os átomos e o campo eletromagnético são quantizados, é eficaz em determinar as taxas de absorção e emissão. Destaca-se a emissão espontânea. Antes, pela descrição semi-clássica, é entendida através dos coeficientes de Einstein. Agora, pela descrição quântica, fica evidente que decorre da quantização do campo eletromagnético.

Conclui-se, também, que a regra de ouro de Fermi é uma ferramenta adaptável: pode ser utilizada para lidar com transições entre estados discretos e entre estado discreto e conjunto de estados quase-contínuos.