- 1 Introdução
- 2 Coeficientes de Einstein
- 3 Teoria de perturbação dependente do tempo
- 4 Aproximação de primeira ordem
- 5 Transição causada por perturbação constante
- 6 Transição causada por perturbação periódica
- 7 Transição causada por fonte contínua
- 8 Transições no átomo de hidrogênio
- 9 Transições no poço infinito
- 10 Mini-banda de transição
- 11 Conclusão
- Referências
1 Introdução
É comum ouvir falar sobre emissão ou absorção de fótons pela matéria.
Há dois tipos de emissão: a espontânea e a estimulada. A emissão espontânea, como o nome aponta, acontece de maneira voluntária, sem causa exterior aparente. Por outro lado, a emissão estimulada ocorre quando um agente externo, como o campo elétrico da radiação eletromagnética, impulsiona a emissão de fótons. Na contramão da emissão estimulada, há a absorção estimulada, em que fótons são tragados pela matéria. Do ponto de vista quântico, a emissão e a absorção ocorrem por causa de transições de estados. Na absorção de fótons, o estado da matéria passa de estados de energia baixa para estados de energia alta, e, na emissão de fótons, o estado da matéria passa de estados de energia alta para estados de energia baixa.
A teoria utilizada para descrever a interação dos fótons com a matéria é chamada de semi-clássica, visto que a radiação é descrita por meio da teoria clássica de Maxwell, enquanto que o estado da matéria é descrito pela teoria quântica de Schrödinger.
Neste artigo vamos estudar a emissão e a absorção de fótons pela matéria. Antes do advento da mecânica quântica, veremos como Albert Einstein esclareceu o assunto e principalmente como criou o conceito de emissão espontânea. A absorção e a emissão também serão estudadas por meio da estrutura da mecânica quântica, tais como equação de Schrödinger e teoria de perturbação dependente do tempo, e fazendo uso de conceitos relacionados com o campo eletromagnético clássico, tais como dipolo elétrico e densidade de energia eletromagnética.
2 Coeficientes de Einstein
O primeiro assunto será sobre a emissão espontânea de fótons pela matéria.
O conceito de emissão espontânea foi “colocado pela mão Einstein” (Einstein 1917). Isso porque, a emissão espontânea não pode ser descrita pela teoria eletromagnética clássica, sendo indispensável a teoria quântica, na qual a radiação eletromagnética vibra como vibram osciladores harmônicos quânticos.

Figura 2.1: Caricatura: Prof. Celso de Araujo Duarte, Departamento de Física (UFPR).
O Prof. Luis Navarro Veguillas, da Facultat de Física, da Universitat de Barcelona, disponibiliza o trabalho original de Einstein, no site Una muestra de trabajos clásicos (os originais em alemão foram substituídos por uma tradução em inglês):
A. Einstein, Zur Quantentheorie der Strahlung (On the Quantum Theory of Radiation), Physikalische Zeitschrift 18, 121-128 (1917); Esse artigo foi reimpresso por D. Ter Haar no livro The Old Quantum Theory, Pergamon Press, Oxford (1967); A primeira versão desse artigo foi publicada em Physikalische Gesellschaft Zürich, Mitteilungen 16, 47-62 (1916).
Vamos lembrar que Schrödinger publicou sua equação em 1926, e a quantização do campo eletromagnético foi realizada pela primeira vez por Dirac (Dirac 1927). Em 1916, Einstein não tratou a emissão por meio da teoria eletromagnética quântica. Atacou o problema de outra maneira. Considerou a matéria em equilíbrio com a radiação, e usou o resultado quântico de Planck, no qual a densidade espectral de energia de radiação obedece a seguinte lei (Planck 1900):
u(ω,T)=ℏω3π2c31exp(ℏω/kBT)−1.
Na equação acima, ℏ é a constante de Planck (reduzida por 2π) [Js], ω é a frequência da radiação [s−1], c é a velocidade da luz [ms−1], kB é a constante de Boltzmann [JK−1], e T é a temperatura [K].
Einstein desenvolveu uma equação para comparar com a equação (2.1) e, assim, deduzir o que hoje é chamado de coeficientes de Einstein.
A partir de agora, os coeficientes de Einstein serão deduzidos.
Vamos usar como apoio à dedução, um sistema que possui dois níveis de energia: E2, será o nível de energia do estado excitado, e E1, o nível de energia do estado fundamental. Um fóton é absorvido por esse sistema se possuir a frequência angular:
ω=E2−E1ℏ.
Ademais, um fóton emitido por esse sistema apresenta essa mesma frequência.
O processo é dinâmico, isso quer dizer que o sitema 2-níveis absorve e emite fótons de maneira ininterrupta. Com uma diferença: só há um tipo de absorção, a absorção estimilada pelo campo de radiação, todavia, há dois tipos de emissão: a espontânea e a estimulada.
Se pensarmos que 1 mol de sitema 2-níveis contém 6×1023 sistemas idênticos, podemos imagimar um recipiente adiabático contendo, por exemplo, um gás de moléculas desse sistema, com n1 moléculas por unidade de volume no nível de energia E1; e n2 moléculas por unidade de volume no nível de energia E2; e também, com fótons de frequência ω, e densidade espectral de energia u(ω). Nessas condições, o número de absorções estimuladas por unidade de tempo por unidade de volume é escrito como B1n1u(ω); e o número de emissões estimuladas por unidade de tempo por unidade de volume é escrito como B2n2u(ω); onde B1 e B2 são os coeficientes de Einstein de absorção e emissão estimulada, respectivamente. As emissões espontâneas são um caso à parte, pois não dependem da radiação que se encontra no recipiente. Então, o número de emissões espontâneas por unidade de tempo por unidade de volume é simplesmente escrito como An2; onde A é o coeficiente de Einstein de emissão espontânea.
O gás de sistema 2-níveis e a radiação que o rodeia estão em equilíbrio termodinâmico. Isso quer dizer que a quantidade de absorções e a quantidade de emissões são iguais:
B1n1u(ω)=B2n2u(ω)+An2.
Manipulando a equação acima, chega-se ao resultado:
u(ω)=An1n2B1−B2.
O próximo passo é lembrar que a razão entre o número de moléculas pode ser descrita pela lei de Boltzmann:
n1n2=exp(ℏωkBT).
Substituindo a equação acima na equação (2.4), tem-se:
u(ω)=AB1exp(ℏω/kBT)−B2.
Por fim, ao comparar a equação que Planck deduzio (2.1), com a equação que Einstein deduzio (2.6), obtém-se que B1=B2, e que:
A=ℏω3π2c3B.
Os coeficientes B1 e B2 serem iguais a um certo B, significa que a probabilidade de ocorrer absorção estimulada é igual à probabilidade de ocorrer emissão estimulada.
O coeficiente A ser função do coeficiente B, significa que a probabilidade de emissão espontânea pode ser maior ou menor que probabilidade de emissão estimulada, e quem influencia diretamente essa competição, é a frequência da radiação ω, definida em (2.2). Isso nos faz concluir:
Se o gap entre os níveis de energia for grande, a emissão espontânea prevalece sobre a estimulada; se for pequeno, a emissão estimulada cresce em importância.
Competição entre emissão espontânea e estimulada
Cada molécula irradia conforme sua estrutura. Pode acontecer da radiação emitida surgir na região do visível, por exemplo, ao redor da cor verde, de frequência fVIS=600×1012 Hz. Outras podem aparecer no infravermelho, por exemplo, a ligação C-H emite ao redor de fIR=90×1012 Hz.
Analisando a relação (2.6), a proporção entre o número de emissões espontâneas e estimuladas é dada por:
R=ABu(ω)=exp(ℏω/kBT)−1.
Tomando a temperatuta T=1000 K:
RVIS=3.2×1012,RIR=74.
Assim, a radiação de molécula quente que irradia no visível é dominada por transições espontâneas; enquanto que não há superioridade na molécula que irradia no infravemelho, porque as transições estimuladas se equiparam com as espontâneas.
O comportamento (2.9) também pode ser entendido pela leitura dos valores das energia das respectivas transições:
hfVIS=3.98×10−19 J,hfIR=0.60×10−19 J.
Como se vê, (2.9) e (2.10) confirmam o raciocínio:
Se a distância entre os níveis de energia for grande, a emissão espontânea prevalece sobre a estimulada; se for pequena, a emissão estimulada cresce em importância.
Os coeficientes de Einstein não possuem as mesmas unidades.
Se An2 representa o número de moléculas realizando emissões espontâneas por unidade de tempo por unidade volume, e n2 representa número de moléculas por unidade volume, a unidade do coeficiente A é:
[A]→1s.
O inverso de A tem unidade de tempo e é interpretado como tempo de duração da emissão espontânea. É o tempo que leva para ocorrer a transição espontânea (2→1). Visto ser o tempo para “esvaziar” o estado excitado, pode ser interpretado como tempo de vida do estado excitado em transição espontânea. Para qualquer das interpretações, defini-se esse tempo como:
tA=1A.
Para fazer aparecer as unidades do coeficiente B, é apropriado reescrever (2.7):
B=π2c3ℏω3A.
Substituindo as unidades das grandezas:
[B]→m3Js2.
O tempo de duração da transição estimulada está vinculado à densidade espectral de energia da radiação estimuladora. Por definição, u(ω) tem as unidades de energia por unidade de volume por unidade de intervalo de frequência:
[u(ω)]→Jm3s−1.
Fica claro que o produto Bu(ω) tem unidade de s−1. Nesse sentido, pode-se definir o tempo de vida do estado excitado, sob a influência da radiação ω, como:
tB=1B×1u(ω).
Vamos continuar resolvendo o problema anterior, mas, agora, do ponto de vista dos tempos das transições.
Substituindo as definições (2.12) e (2.16) na equação (2.8), o tempo de emissão estimulada se relaciona com o tempo de emissão espontânea:
tBtA=exp(ℏω/kBT)−1.
Então, molécula quente que emite no visível possui tB(ωVIS)≫tA, enquanto outra que emite no infravermelho apresenta tB(ωIR)≈tA.
3 Teoria de perturbação dependente do tempo
Os coeficientes de Einstein ajudam a entender a competição entre emissões estimuladas e espontâneas. Todavia, o assunto ainda está um pouco vago, pois não há expressões que liguem A e B ao interior do átomo. É necessário dar um passo adiante, trazendo para a discussão conceitos da mecânica quântica. Einstein usou um princípio da mecânica quântica na dedução de seus coeficientes: o da quantização da energia, embutido por Planck quando deduzio sua lei, equação (2.1). Agora, vamos abrir a “caixa de ferramentas e colocar sobre a mesa valiosos instrumentos de trabalho.” Começaremos “desencaixando” a teoria de perturbação dependente do tempo, de Paul A. M. Dirac, desenvolvedor de teoria da mecânica quântica (Dirac 1926). Você pode baixar o artigo original no site Una muestra de trabajos clásicos.
A técnica de perturbar algo é utilizada quando esse algo não pode ser resolvido de maneira exata. Há solução de outro problema, representado pelo hamiltoniano H0, mas, deseja-se obter a solução do problema representado pelo hamiltoniano H.
Na teoria de perturbação dependente do tempo, perturba-se o hamiltoniano não-perturbado por um termo que se modifica com o tempo:
H(t)=H0+h(t).
Fica claro que se o termo perturbativo for ajustado em h(t)=0, o problema volta a ser não-perturbado.
O problema que sabemos resolver tem o aspecto:
iℏ∂Ψ0(t)∂t=H0Ψ0(t).
Trata-se da equação de Schrödinger dependente do tempo, mas com uma particularidade: o potencial só depende da posição, implicando que a solução pode ser escrita como produto de uma parte estacionária e outra temporal:
Ψ0(t)=∑nc0nφ0ne−iE0nt/ℏ.
A parte estacionária é solução da equação de Schrödinger indenpendente do tempo:
H0φ0n=E0nφ0n.
Nota: O zero colocado acima das grandezas não é para indicar a operação matemática “um número elevado a zero é igual a 1,” mas é para deixar claro que as grandezas fazem parte do problema não-perturbado.
De outra parte, o problema que desejamos resolver tem o aspecto:
iℏ∂Ψ(t)∂t=H(t)Ψ(t);
que tem solução expandida na base das autofunções estacionárias {φ01,φ02,φ03,…}:
Ψ(t)=∑ncn(t)φ0ne−iE0nt/ℏ.
Agora começa um trabalho puramente matemático. Visando determinar os coeficientes cn(t), há necessidade de substituir a expanção (3.6) na equação de Schrödinger (3.5), lembrando que H(t) tem a forma (3.1):
iℏ(∑ndcndtφ0ne−iE0nt/ℏ+∑n−iE0nℏcnφ0ne−iE0nt/ℏ)=∑n[H0+h(t)]cnφ0ne−iE0nt/ℏ.
Usando (3.4):
iℏ∑ndcndtφ0ne−iE0nt/ℏ+∑nE0ncnφ0ne−iE0nt/ℏ=∑n[E0+h(t)]cnφ0ne−iE0nt/ℏ.
Após o cancelamento de termos:
iℏ∑ndcndtφ0ne−iE0nt/ℏ=∑nh(t)cnφ0ne−iE0nt/ℏ.
Nesse ponto, pode-se selecionar uma autofunção da base de autofunções estacionárias para realizar o produto escalar com a equação acima. Vamos imaginar que a escolhida seja a centésima. Nesse caso:
⟨φ0100|φ0n⟩=0,⟨φ0100|φ0100⟩=1.
Então:
iℏ∑ndcndt⟨φ0100|φ0n⟩e−iE0nt/ℏ=∑ncn⟨φ0100|h(t)|φ0n⟩e−iE0nt/ℏ.
O que resulta em:
iℏdc100dte−iE0100t/ℏ=∑ncn⟨φ0100|h(t)|φ0n⟩e−iE0nt/ℏ.
Ou:
iℏdc100(t)dt=∑ncn(t)⟨φ0100|h(t)|φ0n⟩ei(E0100−E0n)t/ℏ.
Antes de resolver essa equação, vamos interpretar o coeficiente c100(t). Ele aparece pela primeira vez na expansão (3.6):
Ψ(t)=c1(t)φ01e−iE01t/ℏ+c2(t)φ02e−iE02t/ℏ+⋯+c100(t)φ0100e−iE0100t/ℏ+⋯
Diante do exposto:
|c100(t0)|2 é a probabilidade do estado estacionário φ0100, de energia E100, estar ocupado no instante t0.
c100(t0) é a amplitude de probabilidade de ocupação do estado (n=100), no tempo t0.
|c100(t0)|2 também pode ser interpretado como probabilidade de transição entre estados, no tempo t0, sendo o estado final o estado (n=100).
A equação (3.13) foi desenvolvida para a ocupação do centésimo estado, mas ela vale para qualquer outro estado n.
O caso de estudo é um sistema de dois níveis. Substituindo “100” por “2,” a probabilidade de ocupação do estado excitado (n=2) é determinada por:
iℏdc2dt=c1(t)⟨φ02|h(t)|φ01⟩ei(E02−E01)t/ℏ+c2(t)⟨φ02|h(t)|φ02⟩ei(E02−E02)t/ℏ.
Ou:
iℏdc2dt=c1(t)⟨φ02|h(t)|φ01⟩eiω21t+c2(t)⟨φ02|h(t)|φ02⟩.
Sendo a frequência de transição definida como:
ω21=E02−E01ℏ.
Nota: ⟨φ02|h(t)|φ01⟩ é o elemento da matriz de transição, o qual conecta o estado inicial (n=1) ao final (n=2); em uma experiência de absorção.
Analogamente, substituindo “100” por “1,” a probabilidade de ocupação do estado fundamental (n=1) é determinada por:
iℏdc1dt=c1(t)⟨φ01|h(t)|φ01⟩ei(E01−E01)t/ℏ+c2(t)⟨φ01|h(t)|φ02⟩ei(E01−E02)t/ℏ.
Ou:
iℏdc1dt=c1(t)⟨φ01|h(t)|φ01⟩+c2(t)⟨φ01|h(t)|φ02⟩e−iω21t.
Nota: ⟨φ01|h(t)|φ02⟩ é outro elemento da matriz de transição, nesse caso, conecta o estado inicial (n=2) ao final (n=1); em uma experiência de emissão estimulada.
As equações (3.16) e (3.19) nos ajudam a responder uma questão importante: Se inicialmente o sistema 2-níveis está no estado fundamental, qual é a probabilidade dele subir para o estado excitado, no tempo t? E se inicialmente o sistema está no estado excitado, qual é a probabilidade dele baixar para o fundamental, no tempo t?
As próximas seções vão aprofundar as questões acima. Por hora, vamos fazer um teste radical: deligar a perturbação, fazendo h(t)=0. É evidente que c1(t) e c2(t) são constantes. Os valores poderiam ser c1(t)=c1(0)=1 e c2(t)=c2(0)=0, indicando que o estado ocupado estará sempre ocupado, e que não há probabilidade do estado vazio ser ocupado. Como não há perturbação, esses estados permaneceriam assim para sempre!
4 Aproximação de primeira ordem
Vamos expandir c2(t) em uma série de potências que depende de certo parâmetro X:
c2=X0c(0)2+X1c(1)2+X2c(2)2+⋯.
Fazer o mesmo para c1(t):
c1=X0c(0)1+X1c(1)1+X2c(2)1+⋯.
Substituir as séries truncadas em primeira ordem na equação (3.16) (por conveniência, o método de trabalho também acrescenta o parâmetro na perturbação):
iℏd[c(0)2+Xc(1)2]dt=[c(0)1+Xc(1)1]⟨φ02|Xh(t)|φ01⟩ei(E02−E01)t/ℏ+[c(0)2+Xc(1)2]⟨φ02|Xh(t)|φ02⟩.
Ou:
iℏd[c(0)2+Xc(1)2]dt=[Xc(0)1+X2c(1)1]⟨φ02|h(t)|φ01⟩ei(E02−E01)t/ℏ+[Xc(0)2+X2c(1)2]⟨φ02|h(t)|φ02⟩.
Agrupar os termos que possuem a potência X:
iℏd[Xc(1)2]dt=[Xc(0)1]⟨φ02|h(t)|φ01⟩ei(E02−E01)t/ℏ+[Xc(0)2]⟨φ02|h(t)|φ02⟩.
Cancelar o parâmetro X:
iℏdc(1)2dt=c(0)1⟨φ02|h(t)|φ01⟩ei(E02−E01)t/ℏ+c(0)2⟨φ02|h(t)|φ02⟩.
É fácil concluir que os coeficientes de ordem (0) não se modificam com o tempo, por exemplo, dc(0)2/dt=0 em (4.4). Podemos, então, considerar que antes da perturbação, o estado 1 está ocupado, quer dizer, que c(0)1 sempre será c(0)1=1, e também considerar que o estado 2 está vazio, ou seja, que c(0)2 sempre será c(0)2=0. Nesse caso:
dc(1)2dt=1iℏ⟨φ02|h(t)|φ01⟩ei(E02−E01)t/ℏ.
Se a perturbação começa em t=0, a solução da equação acima é:
c(1)2(t)=1iℏ∫t0dt′⟨φ02|h(t′)|φ01⟩ei(E02−E01)t′/ℏ.
5 Transição causada por perturbação constante
Solução de primeira ordem
Martelar o ferro na bigorna gera calor (emissão de radiação infravermelha). A batida (perturbação mecânica) dura um curto intervalo de tempo e, grosso modo, pode ser considerada constante nesse intervalo. Outro tipo de perturbação que não varia com o tempo, envolve aplicar um campo constante na matéria (elétrico ou magnético).
Vamos representar a perturbação constante escrevendo h(t′)=V, para 0<t′<t, sendo V uma energia potencial constante. Isso facilita o manejo da equação (4.8), pois o termo perturbativo sai da integral:
c(1)2(t)=1iℏ⟨φ02|V|φ01⟩∫t0dt′ei(E02−E01)t′/ℏ=1iℏ⟨φ02|V|φ01⟩1i(E02−E01)/ℏ(ei(E02−E01)t/ℏ−1)=−⟨φ02|V|φ01⟩E02−E01(ei(E02−E01)t/ℏ−1)×2ie−i(E02−E01)t/2ℏ2ie−i(E02−E01)t/2ℏ=−⟨φ02|V|φ01⟩E02−E01(ei(E02−E01)t/2ℏ−e−i(E02−E01)t/2ℏ2i)×2ie−i(E02−E01)t/2ℏ=−⟨φ02|V|φ01⟩E02−E01×sin[12ℏ(E02−E01)t]×2i×ei(E02−E01)t/2ℏ.
Então, a probabilidade de transição causada por perturbação constante é:
|c(1)2(t)|2=|⟨φ02|V|φ01⟩|2×(sin[12ℏ(E02−E01)t]12(E02−E01))2.
Em função do tempo, a probabilidade de ocupação do estado excitado, ou a probabilidade de estar no estado inicialmente vazio, ou a “probabilidade de alcançar o desconhecido,” é uma função senoidal oscilante. Em consequência, a probabilidade de ocupação do estado fundamental também é uma função oscilante, pois:
|c1(t)|2=1−|c2(t)|2.
Vendo a Fig. 5.1, isso parece inacreditável, já que o estado de transição:
Ψ(t)=c1(t)φ01e−iE01t/ℏ+c2(t)φ02e−iE02t/ℏ=c1(t)Φfundamental+c2(t)Φexcitado,
oscila entre estar no estado fundamental e estar no excitado!
Todavia, tem um significado físico acreditável: Dá a entender que, enquanto durar a perturbação, o sistema absorve e emite energia de modo cíclico:
↗excitado↘fundamental↗excitado↘fundamental.
↗absorve↘emite↗absorve↘emite.
Uma imagem mental apropriada seria a de uma “metralhadora de fótons” que carrega e atira sem parar, ou enquanto durar o “carregador” (perturbação).

Figura 5.1: Probabilidade de ocupação do estado excitado (linha sólida) e do fundamental (linha tracejada), de um sistema de dois níveis, submetido a uma perturbação constante.
A função seno tem máximo em π/2.
O máximo da função (5.2) ocorre em:
12ℏ(E02−E01)t=π2.
E o tempo de probabilidade de transição máxima é:
tmax=πℏE02−E01.
Nesse tempo:
|c(1)2(tmax)|2=|⟨φ02|V|φ01⟩|2×4(E02−E01)2.
No outro extremo:
|c(1)2(2tmax)|2=0.
Solução exata
As equações diferenciais acopladas (3.16) e (3.19) podem ser resolvidas sem aproximação, desse modo, é possível encontrar uma expressão exata para a probabilidade de transição causada por perturbação constante.
Damos início modificando a notação por uma mais simples:
˙c=dcdt;
e:
⟨φ02|V|φ01⟩=ℏv,⟨φ02|V|φ02⟩=0,⟨φ01|V|φ02⟩=ℏv∗,⟨φ01|V|φ01⟩=0.
Com isso, as equações acima citadas se tormam:
˙c2=−ivc1eiω21t,˙c1=−iv∗c2e−iω21t.
As derivadas resultam em:
¨c2=−iv˙c1eiω21t+ω21vc1eiω21t,¨c1=−iv∗˙c2e−iω21t−ω21v∗c2e−iω21t.
Ou:
¨c2=−|v|2c2+iω21˙c2,¨c1=−|v|2c1−iω21˙c1.
Ou:
¨c2−iω21˙c2+|v|2c2=0,¨c1+iω21˙c1+|v|2c1=0.
O objetivo agora é resolver a equação diferencial referente ao caso excitado, para poder comparar com o resultado do caso excitado de primeira ordem [equação (5.2), copiada logo abaixo com nova notação]:
|c(1)2(t)|2=|v|2(sin[12ω21t]12ω21)2.
Primeiro, assume-se que a solução da primeira equação (5.14) é do tipo:
c2(t)=eiΩt.
É fácil verificar que essa solução gera a seguinte equação de segundo grau:
Ω2−ω21Ω−|v|2=0,
com resolução:
Ω=ω21±√ω221+4|v|22=ω21±Ω02,
chamando:
Ω0=√ω221+4|v|2.
Conclui-se que (5.16) carrega dois termos:
c2(t)=eiω21t/2[AeiΩ0t/2+Be−iΩ0t/2],
As condições iniciais são: Em t=0, o estado fundamental está ocupado e o excitado está vazio, quer dizer, c1(0)=1 e c2(0)=0.
Substituindo a condição inicial do estado excitado em (5.20), observa-se que B=−A, sendo assim:
c2(t)=Aeiω21t/2[eiΩ0t/2−e−iΩ0t/2]=Aeiω21t/2×sin(Ω0t/2)×2i.
Para determinar A, nota-se que ˙c2(0)=AΩ0i, ademais, segundo a equação (5.11), ˙c2(0)=−ivc1(0), portanto:
A=−vΩ0.
Por fim:
c2(t)=−vΩ0eiω21t/2×sin(Ω0t/2)×2i.
O que resulta em:
|c2(t)|2=|v|2(sin[12Ω0t]12Ω0)2.
Conclui-se que o resultado de primeira ordem (5.15) e o exato (5.24) possuem a mesma estrutura. Só diferem na expressão da frequência de oscilação entre estado excitado populado e estado excitado depopulado. Ademais, se o efeito da perturbação for pequeno, pode ocorrer Ω0≈ω21, conforme sugere (5.19).
Nota: Pode-se repetir o procedimento para se obter |c1(t)|2, todavia, é mais conveniente usar o fato que |c1(t)|2=1−|c2(t)|2.
6 Transição causada por perturbação periódica
A probabilidade de transição de um sistema de 2 níveis na presença de um campo elétrico que oscila harmonicamente com frequência angular ω, será determinada. Um elétron com vetor de posição →r em relação ao núcleo atômico, e carga q=−e, será considerado. Um vetor de dipolo elétrico →p=q→r=−e→r, fará parte da interação elétron/campo. Essa interação produz energia h(t)=−→E(t)⋅→p; o sinal de menos faz parte da fórmula.
O campo está na direção do vetor de polarização →ϵ (um vetor unitário):
→E(t)=→ϵE0cos(ωt).
Então, a energia que perturba o sistema é:
h(t)=(→ϵ⋅→r)eE0cos(ωt).
Ou:
h(t)=h0(eiωt+e−iωt);
chamando h0=12(→ϵ⋅→r)eE0.
Com restrições
O problema será resolvido com a equação (3.16) e duas restrições: (1) o coeficiente do estado fundamental permanerá próximo de 1; (2) o coeficiente do estado excitado não se afastará muito de 0; durante a atuação da perturbação.
Vamos, então, fazer c1(t)=1 e c2(t)=0 do lado direito da equação (3.16):
˙c2(t)=1iℏ⟨φ02|h(t)|φ01⟩eiω21t.
Agora, substituir a perturbação (6.3) na equação acima:
c2(t)=1iℏ⟨φ02|h0|φ01⟩∫t0dt′(eiωt′+e−iωt′)eiω21t′=1iℏ⟨φ02|h0|φ01⟩(ei(ω21+ω)t−1i(ω21+ω)+ei(ω21−ω)t−1i(ω21−ω)).
Vamos trabalhar o primeiro termo do parênteses:
T1=ei(ω21+ω)t−1i(ω21+ω)×2e−i(ω21+ω)t/22e−i(ω21+ω)t/2=sin[12(ω21+ω)t](ω21+ω)×2e−i(ω21+ω)t/2=sin[12(ω21+ω)t]12(ω21+ω)×ei(ω21+ω)t/2.
Analogamente, o segundo termo do parênteses é:
T2=sin[12(ω21−ω)t]12(ω21−ω)×ei(ω21−ω)t/2.
Com a releitura:
c2(t)=−iv0(sin[12(ω21+ω)t]12(ω21+ω)ei(ω21+ω)t/2+sin[12(ω21−ω)t]12(ω21−ω)ei(ω21−ω)t/2);
chamando:
ℏv0=⟨φ02|h0|φ01⟩=⟨φ02|12(→ϵ⋅→r)eE0|φ01⟩=12eE0⟨φ02|(→ϵ⋅→r)|φ01⟩=12eE0cosθ⟨φ02|→r|φ01⟩;
onde θ é o ângulo entre o vetor de polarização e vetor de posição do elétron; o que implica em:
|v0|2=e2[E0]2[cosθ]24ℏ2|⟨φ02|→r|φ01⟩|2;
onde ⟨φ02|→r|φ01⟩ é o raio de trasição.
Em (6.8), a frequência da transição (ω21) tem valor fixo. A varredura pode ser feita na frequência do campo (ω). Quando ω→ω21, ocorre um pico acentuado no termo T2, fazendo o termo T1 ser despresível. Nesse caso:
c2(t)=−iv0(sin[12(ω21−ω)t]12(ω21−ω)ei(ω21−ω)t/2).
O que resulta em:
|c2(t)|2=|v0|2(sin[12(ω21−ω)t]12(ω21−ω))2.
Essa equação não é estranha! Sua estrutura já apareceu outras vezes no texto: ver (5.15) e (5.24). A novidade é que a oscilação entre estado excitado populado e estado excitado depopulado se dá em função da frequência do campo elétrico aplicado (gerado por um laser, por exemplo).
É importante endender o significado prático da equação (6.12). Ela mostra que para um corpo absorver luz monocromática, a frequência de excitação (ω) deve estar bem próxima da frequência de transição (ω21). Caso isso não ocorra, a ocupação do estado excitado será ineficiente, pois a probabilidade de transição será quase zero. Por outro lado, se a frequência de excitação for bem próxima da frequência de transição, a ocupação do estado excitado será fortemente favorecida pelo fato da probabilidade de transição, com o tempo fixo, apresentar um pico ao redor de ω=ω21.

Figura 6.1: Probabilidade de ocupação do estado excitado, de um sistema de dois níveis, submetido a uma perturbação periódica.
Sem restrições
Agora vamos resolver as equações acopladas (3.16) e (3.19), como fizemos na Seção 5 (solução exata). Visto que as passagnes são as mesmas, basta fazer algumas adaptações.
A principal alteração se dá no elemento da matriz de transição:
⟨φ02|h(t)|φ01⟩=⟨φ02|h0(eiωt+e−iωt)|φ01⟩=⟨φ02|h0|φ01⟩(eiωt+e−iωt).
Chamando:
⟨φ02|h0|φ01⟩=ℏv,⟨φ01|h0|φ02⟩=ℏv∗,
obtém-se:
⟨φ02|h(t)|φ01⟩=ℏv(eiωt+e−iωt),⟨φ01|h(t)|φ02⟩=⟨φ02|h(t)|φ01⟩∗=ℏv∗(e−iωt+eiωt).
Assim, a primeira equação (5.11) se torna:
˙c2=−iv(eiωt+e−iωt)c1eiω21t.
O que implica em:
c1=˙c2−ivei(ω21+ω)t−ivei(ω21−ω)t.
Analisando o denominador, percebe-se que o coeficiente c1 é dominado pelo termo ei(ω21−ω)t (o outro termo pode ser desprezado). Isso equivale a perturbar o sistema com o potencial periódico h(t)=h0e−iωt, com h0=(→ϵ⋅→r)eE0.
Vamos, então, trabalhar com o novo potencial na matriz de transição:
⟨φ02|h(t)|φ01⟩=ℏve−iωt,⟨φ01|h(t)|φ02⟩=ℏv∗eiωt.
A continuação é um trabalho puramente matemático. Porém, analisando as passagens da Seção 5 (solução exata), fica claro que deve-se ajustar (5.23), trocando (ω21) por (ω21−ω):
c2(t)=−vΩ0ei(ω21−ω)t/2×sin(Ω0t/2)×2i,
com:
Ω0=√(ω21−ω)2+4|v|2.
O que resulta em:
|c2(t)|2=|v|2(sin[12Ω0t]12Ω0)2.
Atenção: O Ω0 dessa seção e o Ω0 da Seção 5 são diferentes: veja (5.19).
Neste ponto, podemos estudar um caso especial: Considerar a frequência da perturbação exatamente igual à frequência de transição (ω=ω21). Nesse caso, a probabilidade de transição se torna:
|c2(t)|2=sin2(t√|v|2).
Isso mostra que, enquanto durar a perturbação, o sistema absorve e emite energia de modo cíclico.
Nota: Considerar (ω=ω21) no resultado “com restrições,” equação (6.12), leva a outra conclusão! A oscilação de |c2(t)|2 desaparece. É como se a “metralhadora de fótons” deixasse de existir! Isso porque usar “restrições” simplifica o problema e limita o resultado (equivale a trabalhar com aproximação de primeira ordem).
7 Transição causada por fonte contínua
Um laser produz radiação eletromagnética com frequência bem definida. Outras fontes, como um filamento incandescente, produzem uma sucessão contínua de frequências.
A probabilidade de transição causada por fonte contínua é determinada somando-se a probabilidades de transição de cada frequência.
O ponto de partida é a equação (6.12):
|c2(t)|2=e2[E0]2[cosθ]24ℏ2|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ω)t]12(ω21−ω))2.
Como a fonte contínua possui uma sucessão de frequências ωi, essa equação pode ser adaptada para cada modo de vibração eletromagnético:
|c2(t)|2(modo i)=e2[E0(ωi)]2[cosθ]24ℏ2|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ωi)t]12(ω21−ωi))2.
A relação entre a densidade de energia e a amplitude do campo elétrico é:
U(ωi)=12ϵ0[E0(ωi)]2.
ϵ0 é a permissividade do vácuo [C2J−1m−1].
A substituir a equação acima na anterior:
|c2(t)|2(modo i)=e2[2U(ωi)ϵ0][cosθ]24ℏ2|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ωi)t]12(ω21−ωi))2.
Deve-se realizar a somatória para determinar a probabilidade de transição total:
∑i|c2(t)|2(modo i)=∑iU(ωi)e2[cosθ]22ℏ2ϵ0|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ωi)t]12(ω21−ωi))2.
A chamar a probabilidade de transição total de P2(t) e transformar a somatória em integral:
P2(t)=1dω∫dω U(ω)e2[cosθ]22ℏ2ϵ0|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ω)t]12(ω21−ω))2.
A relação entre a densidade de energia e a densidade espectral de energia é:
U(ω)=u(ω)dω.
A substituir a equação acima na anterior:
P2(t)=∫dω u(ω)e2[cosθ]22ℏ2ϵ0|⟨φ02|→r|φ01⟩|2(sin[12(ω21−ω)t]12(ω21−ω))2.
Essa integral pode ser simplificada usando a aproximação u(ω)≈u(ω21), pois o campo quase não se modifica ao redor do pico da Fig. 6.1:
P2(t)=u(ω21)e2[cosθ]22ℏ2ϵ0|⟨φ02|→r|φ01⟩|2∫dω (sin[12(ω21−ω)t]12(ω21−ω))2.
O valor da última integral é 2πt:
P2(t)=u(ω21)e2[cosθ]22ℏ2ϵ0|⟨φ02|→r|φ01⟩|2×2πt.
Esse resultado ainda pode levar em conta todos ângulos entre o vetor de polarização e o vetor posição, lembrando que ¯[cosθ]2=1/3:
P2(t)=πe23ℏ2ϵ0×u(ω21)×|⟨φ02|→r|φ01⟩|2×t.
A taxa de transição, que será representada por W, é a probabilidade de transição por unidade de tempo. É determinada fazendo a derivada da probabilidade de transição no tempo. No caso da equação acima, a taxa de transição total é:
W2=πe23ℏ2ϵ0×u(ω21)×|⟨φ02|→r|φ01⟩|2.
Não há necessidade de repetir o procedimento para resolver o caso da transição que inicia no estado excitado e termina no fundamental, pois, a taxa de ocupação do estado excitado (em uma experiência de absorção estimulada por campo) é igual a taxa de ocupação do estado fundamental (em uma experiência de emissão estimulada por campo), ou seja: W2=W1.
Agora vamos voltar a falar sobre os coeficientes da Seção 2.
O coeficiente de Einstein de absorção (ou emissão) estimulada se escreve:
B=W2u(ω21)=πe23ℏ2ϵ0×|⟨φ02|→r|φ01⟩|2.
Então, utilizando a relação (2.7), o coeficiente de Einstein de emissão espontânea é:
A=ℏω321π2c3×B=ℏω321π2c3×πe23ℏ2ϵ0×|⟨φ02|→r|φ01⟩|2=e2ω3213πc3ℏϵ0×|⟨φ02|→r|φ01⟩|2.
Nota: O coeficiente A é equivalente à taxa de transição de emissão espontânea; com unidade s−1.
Agora os coeficientes de Einstein estão vinculados ao interior do átomo, por meio do termo puramente quântico |⟨φ02|→r|φ01⟩|2.
Segundo (2.12), a duração da transição espontânea é:
tA=3πc3ℏϵ0e2ω321×1|⟨φ02|→r|φ01⟩|2.
Isso quer dizer que o estado excitado permanece “vivo” por tA (segundos), antes de ficar totalmente depopulado por emissão espontânea.
Segundo (2.16), ou segundo [ Eq. (7.12) ]−1, a duração da transição estimulada é:
tB=3ℏ2ϵ0πe2×1|⟨φ02|→r|φ01⟩|2×1u(ω21).
Isso quer dizer que o estado excitado permanece “vivo” por tB (segundos), antes de ficar totalmente depopulado por emissão estimulada; ou, que o estado fundamental permanece “vivo” por tB (segundos), antes de ficar totalmente depopulado por absorção estimulada.
A relação entre os tempos acima é:
tBtA=ℏω321π2c3×1u(ω21)=AB×1u(ω21).
8 Transições no átomo de hidrogênio
O átomo mais simples que existe na natureza é o átomo de hidrogênio, formado com 1-elétron orbitando em torno de 1-próton (núcleo). Se for definido o nível de energia do estado fundamental (n=1) como sendo o nível zero, o primeiro estado excitado (n=2) está no nível 10.2 eV. Nesse caso, a frequência da transição (1→2) é:
ω21=10.2 eVℏ=10.2 eV6.5821×10−16 eVs=15497×1012 s−1.
Ou:
f21=ω212π=2466×1012 Hz.
Ou:
λ21=cf21=121.6×10−9 m.
Comparando com a frequência óptica fvioleta=800×1012 Hz, a transição (1→2) do átomo de hidrogênio ocorre na região do ultravioleta (invisível aos olhos humanos).
O primeiro estado excitado do átomo de hidrogênio, capaz de fazer transição com o estado fundamental, é degenerado em energia (como dito, está 10.2 eV acima do fundamental). É constituído dos orbitais 2px, 2py e 2pz.
A soma das funções de onda 1√2(ψ21−1−ψ211) é o orbital:
2px=1√32π(Za)52re−Zr/2asinθcosϕ.
A soma das funções de onda i√2(ψ21−1+ψ211) é o orbital:
2py=1√32π(Za)52re−Zr/2asinθsinϕ.
Onde:
ψ211=−1√64π(Za)52re−Zr/2asinθeiϕ,ψ21−1=1√64π(Za)52re−Zr/2asinθe−iϕ.
De outra formação, o orbital 2pz não é fruto de superposição, é a própria função de onda ψ210:
2pz=1√32π(Za)52re−Zr/2acosθ.
Por fim, o estado fundamental do átomo de hidrogênio é simplesmente:
1s=1√π(Za)32e−Zr/a.
Nas fórmulas, o número Z é o número atômico, no caso do hidrogênio, Z=1; e a constante a é o raio de Bohr: a=0.53×10−10 m.
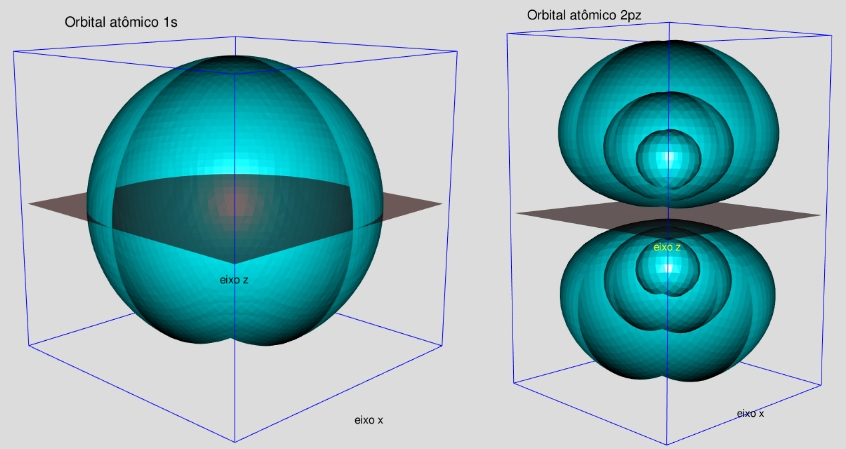
Figura 8.1: Orbitais 1s e 2pz (3 isosuperfícies).
A Fig. 8.1 apresenta os orbitais 1s e 2pz do átomo de hidrogênio. Como se vê, o estado fundamental tem aparência de esfera, e o excitado, de halteres de academia. Isso quer dizer que na transição (2→1), por exemplo, o elétron passa por um processo de reorganização espacial, partindo da forma de halteres e terminando na forma de esfera. Isso leva tempo! As fórmulas (7.15) e (7.16) revelam que os tempos envolvidos são tA e tB, respectivamente. Podemos calcular esses tempos, mas para isso, precisamos calcular:
|⟨φ02|→r|φ01⟩|2=|⟨2px+2py+2pz|→r|1s⟩|2.
O trabalho é puramente matemático, envolve resolver integrias. Entretanto, está descrito com muitos pormenores no livro Introductory Quantum Mechanics, do Prof. Richard Fitzpatrick, hospedado na biblioteca LibreTexts, do projeto de livros didáticos de acesso aberto. O resultado é:
|⟨φ02|→r|φ01⟩|2=215310a2=1.5542×10−21 m2.
Vamos, então, determinar a duração da emissão espontânea (2→1):
tA=3πc3ℏϵ0e2ω321×1|⟨φ02|→r|φ01⟩|2=3π(3×108)3(1.0546×10−34)(8.8542×10−12)(1.6×10−19)2(15497×1012)3×11.5542×10−21=1.5954×10−9 s.
O tempo de absorção (2←1) é igual ao tempo de emissão estimulada (2→1) entretanto, dependem da temperatura através da densidade espectral de energia (2.1):
tB=3ℏ2ϵ0πe2×1|⟨φ02|→r|φ01⟩|2×1u(ω21,T)=3(1.0546×10−34)2(8.8542×10−12)π(1.6×10−19)2×11.5542×10−21×1u(ω21,T)=2.3570×10−21×1u(ω21,T).
A listagem abaixo apresenta tB para vários valores de temperatura:
tB(1000 K)=4.24×1042 stB(5000 K)=30.7 stB(10000 K)=2.22×10−4 stB(15000 K)=4.28×10−6 stB(20000 K)=5.93×10−7 stB(25000 K)=1.80×10−7 stB(30000 K)=8.10×10−8 stB(35000 K)=4.54×10−8 stB(40000 K)=2.92×10−8 stB(45000 K)=2.06×10−8 stB(50000 K)=1.54×10−8 stB(100000 K)=3.62×10−9 s
Em 1000 K, pode-se dizer que não há transição estimulada por campo. Em 5000 K, o tempo ainda é alto, meio minuto. Acima de 10 mil K, a transição estimulada começa a competir com a espontânea. Porém, somente em 100 mil K, os valores se equilibram na casa dos 10−9 segundos.
Dava por encerrada a seção, quando surgiu uma dúvida: Se a frequência do campo está próxima da frequência de transição (em todos os casos), por que nos primeiros casos o tempo da transição foi tão grande? E por que nos últimos casos foi tão pequeno?
Achei que as fórmulas (7.3) e (7.7) poderiam responder essa questão: A amplitude do campo elétrico depende da temperatura por meio da densidade espectral de energia:
12ϵ0E20=∫u(ω,T)dω.
A utilizar a lei de Planck, equação (2.1), a integral foi numericamente calculada para as diversas temperaturas. Em seguida, determinou-se o campo elétrico (N/C):
E0(1000 K)=13073E0(5000 K)=326828E0(10000 K)=1307311E0(15000 K)=2941448E0(20000 K)=5229243E0(25000 K)=8170691E0(30000 K)=11765795E0(35000 K)=16014555E0(40000 K)=20916971E0(45000 K)=26473040E0(50000 K)=32682766E0(100000 K)=130731057
A ocorrer transição estimulada por campo, não basta a frequência do campo estar próxima da frequência de transição, mas também é necessário que a amplitude do campo seja “forte” o suficiente para produzir um “chacoalhão” no estado do elétron. Se a amplitude for muito pequena, mesmo a frequência estando certa, não haverá mudança de estado, pois o tempo de transição parece se tornar “infinito” comparado com a vida de um ser humano. Por outro lado, se a amplitude for grande o suficiente para tirar o elétron de seu estado de conforto, após um curto intervalo de tempo, haverá mudança de estado.
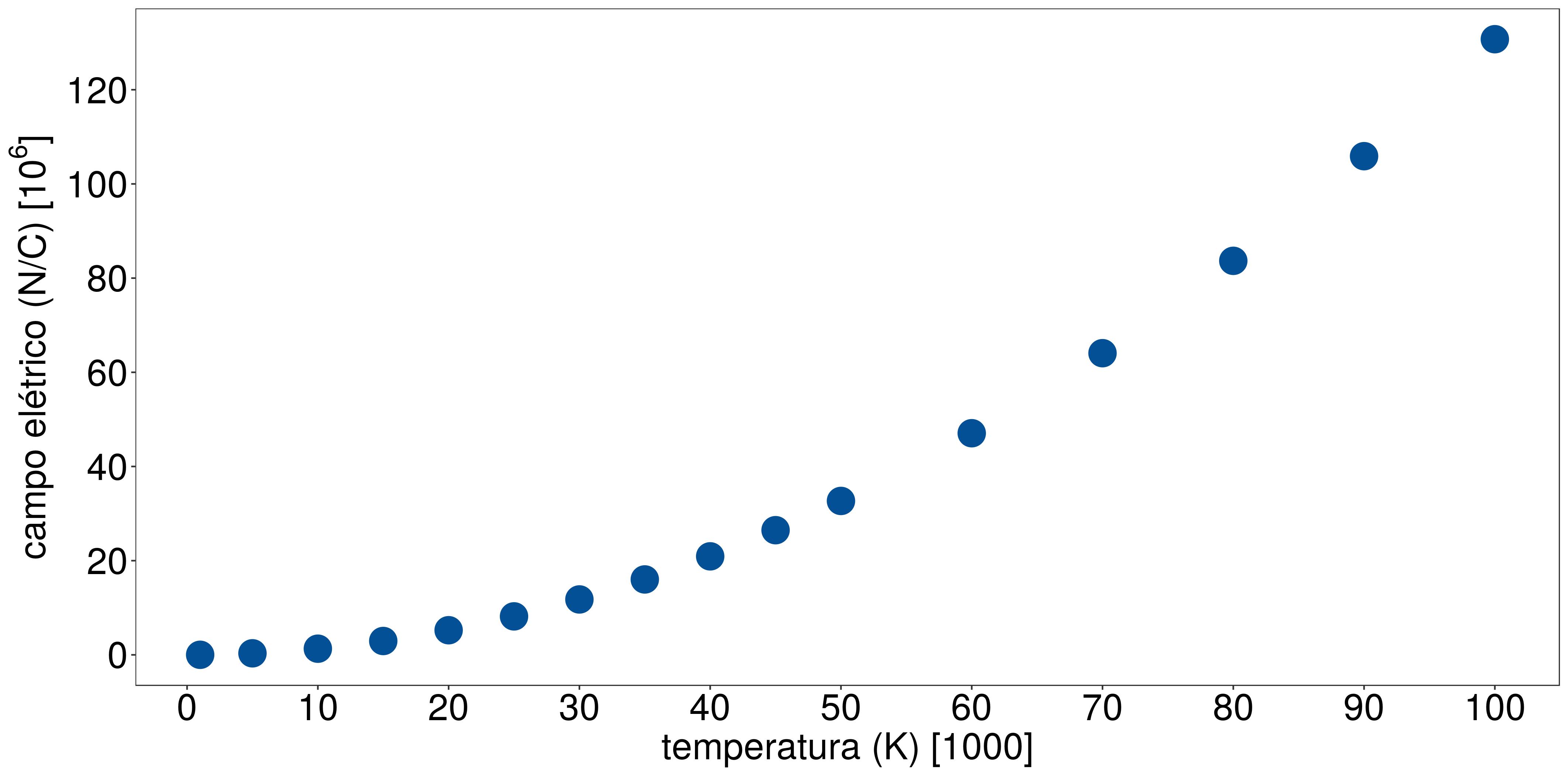
Figura 8.2: Campo elétrico em função da temperatura.
9 Transições no poço infinito
O poço retangular infinito, unidimensional, de largura L, com um elétron de massa me confinado, possui funções de onda e energias dadas por:
φ0n=|n⟩=√2Lsin(nπLx)En=ℏ2π2n22meL2n=1 ,2 ,3…
Vamos usá-lo como exemplo para o estudo da transição estimulada e da espontânea.
Características do poço
A largura do poço é L= 100 Å.
A energia do estado fundamental é E1= 3.76 meV.
A energia do primeiro estado excitado é E2= 15.04 meV.
A diferença entre as energias energia é (E2−E1)= 11.28 meV.
A frequência de transição é ω21= 1.71×1013 s−1.
O raio de transição é ⟨2|x|1⟩=2L∫L0sin(2πLx)xsin(πLx)dx. Resolvendo a integral, ⟨2|x|1⟩= 1.8×10−9 m.
O quadrado do raio de transição é |⟨2|x|1⟩|2= 3.24×10−18 m2.
Características da transição estimulada
As fórmulas se encontram na Seção 7.
Vamos assumir que o elétron está inicialmente no estado fundamental (n=1) e que, no tempo t=0, sofra a ação de uma perturbação periódica produzida por uma sucessão contínua de frequências. Isso faz o elétron subir para o primeiro estado excitado (n=2). Ademais, o elétron e a radiação estão em equilíbrio termodinâmico na temperatuta ambiente. Nessas condições:
O coeficiente de Einstein da transição estimulada é B= 8.86×1023 m3J−1s−2.
A temperatura é T= 300 K.
A densidade espectral de energia é u(ω21,T)= 3.65×10−21 Jsm−3.
A taxa da transição estimulada é W2= 3232.42 s−1.
A duração da transição estimulada é tB= 3.09×10−4 s.
Características da transição espontânea
As fórmulas também se encontram na Seção 7.
Podemos também considerar a situação do elétron estar inicialmente no estado excitado e, no tempo t=0, de maneira voluntária, descer espontaneamente para o fundamental. Então:
A taxa da transição espontânea é A= 1768.47 s−1.
A duração da transição espontânea é tA= 5.65×10−4 s.
A razão entre os tempos é tBtA= 0.55.
10 Mini-banda de transição
Já vimos que, em função do tempo, a probabilidade de transição causada por perturbação periódica é uma função senoidal, oscilante: veja a equação (6.12), a qual tem aparência projetada na Fig. 5.1. Olhando cada ciclo, a curva tem semelhança com uma gaussiana. Então, no ciclo, pode-se aproximar a probabilidade de transição com a seguinte expressão:
|c2(t)|2≈e−t2/τ2.
A equação acima pode ser modelada como uma superposição de ondas planas usando a análise de Fourier:
e−t2/τ2=1√2π∫b(E)e−iEℏtdE.
Mudança de variável:
ω=Eℏ ⟹ dE=ℏdω.
e−t2/τ2=1√2π∫ℏb(ω)e−iωtdω.
O coeficiente da superposição é:
ℏb(ω)=1√2π∫e−t2/τ2eiωtdt.
O que resulta em:
ℏb(ω)=τ√2e−τ24ω2.
Ou:
b(E)=τℏ√2e−τ24ℏ2E2.
O que finalmente resulta em:
|b(E)|2=τ22ℏ2e−τ22ℏ2E2.
Partimos com uma gaussiana no espaço do tempo e terminamos com outra gaussiana no espaço da energia. Este resultado é muito importante! Ele mostra que um estado com tempo de vida finito não possui energia única, mas, sim, mini-banda de transição com energia incerta. Como estimativa, o estado perturbado se distribui pela mini-banda:
δE∝ℏτ,
onde τ é o tempo tA ou tB.
Mini-banda de transição no poço infinito
Substituição dos tempos da Seção 9 na estimativa (10.9) .
Para o tempo tB= 3.09×10−4 s, a incerteza na energia é δEB= 2.13×10−9 meV.
Para o tempo tA= 5.65×10−4 s, a incerteza na energia é δEA= 1.16×10−9 meV.
Quanto maior for o tempo de vida do estado perturbado, menor será a incerteza na energia.
Pode-se estrapolar essa conclusão:
Se o tempo de vida for infinito, a incerteza na energia é zero.
É por isso que fótons coletados em experiência de emissão, apresentam distribuição que se assemelha a uma gaussiana, com largura à meia altura relacionada com o tempo de vida do estado que decai; ou, de outro ponto de vista, relacionada com a mini-band de transição desse estado.
As gaussianas podem ser deslocadas para se adequarem melhor ao problema. Vamos ilustrar o processo da emissão estimulada, todavia, o mesmo modelo é compatível para explicar a absorção. Para simplificar a notação, vamos “enxugar as fórmulas” e trabalhar somente com o contorno das gaussianas:
|c(t)|2≈e−(tB−t)2,|b(E)|2≈e−(Δ21−E)2,
sendo Δ21=E2−E1.
|c(t)|2 representa a probabilidade do estado ser populado no tempo t; e |b(E)|2 representa a probabilidade do canal de energia E participar do processo.
O processo da emissão estimulada é esquenatizado nas Figs. 10.1 e 10.2. Pensando em um quadro mais realista, a perturbação produz mini-bandas nos estados fundamental e excitado. Dentro da faixa, a energia é contínua, mas o desenho mostra apenas 3 canais de transição. No início, em t=tI, a probabilidade do estado ser populado é pequena, e a transição ocorre pelo canal de menor energia, E=ΔI. Quando se chega no tempo caracteristico da transição, t=tB, a probabilidade de transição atinge o valor máximo, e a transição é feita pelo canal de ressonância, E=Δ21. Por fim, em t=tII, a probabilidade de transição volta a ser pequena, e a transição se dá pelo canal de maior energia, E=ΔII.
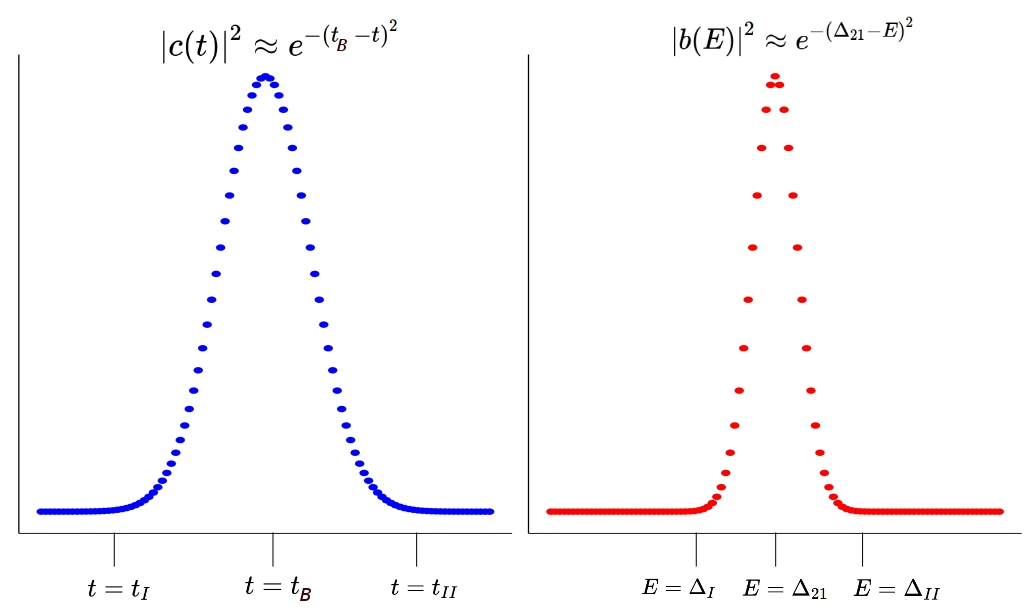
Figura 10.1: Probabilidade de transição (gaussiana no espaço do tempo) e probabilidade de participação (gaussiana espaço da energia).
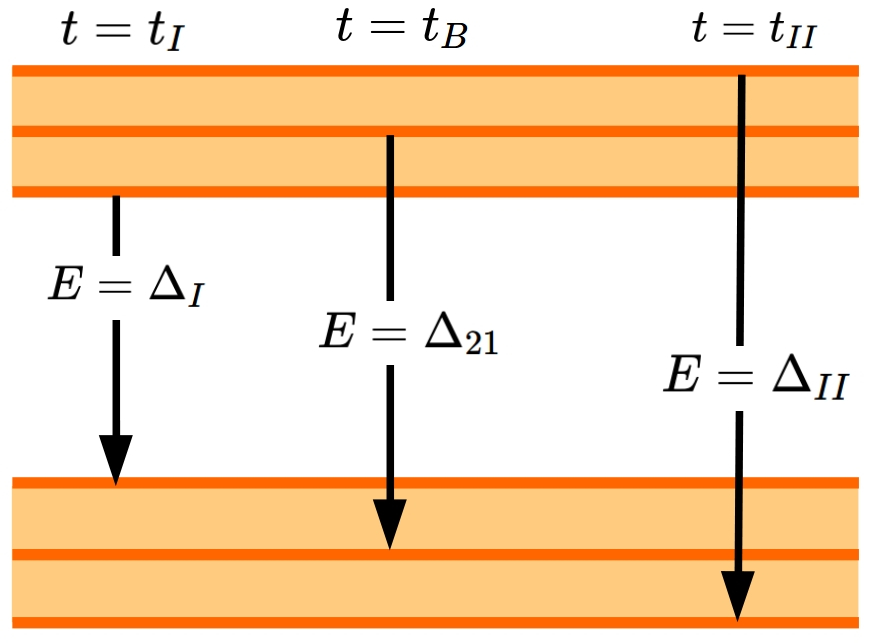
Figura 10.2: Canais de transição entre mini-bandas de transição.
11 Conclusão
As principais conclusão são:
As transições causadas por perturbação constante e por perturbação periódica apresentam probabilidades de transição oscilantes com o passar do tempo. Isso dá a entender que, enquanto durar as perturbações, o sistema absorve e emite energia de modo cíclico.
O estado não-perturbado possui tempo de vida infinito e energia única.
O estado perturbado possui tempo de vida finito e mini-banda de transição. Isso dá a entender que a incerteza na medição da energia de transição não pode ser eliminada por aperfeiçoamento tecnológico de equipamento de medição.
As mini-bandas de transição são responsáveis pela largura à meia altura do espectro de emissão ou absorção.