1 A tempestade

O que quero contar é algo que aconteceu comigo e acredito que também possa acontecer com outras pessoas. Não é sobre alguém estar feliz com o seu time. Mas é sobre alguém estar inquieto com suas pesquisas.

Antes da final da Libertadores da América e depois de ler alguns artigos sobre barras metálicas que se movem em campos magnéticos, entrei num nevoeiro, desses que encobrem as ruas e levam ao fechamento de aeroportos. Acho que esqueci a origem da força eletromotriz (pensei). Será que estou desaprendendo os fundamantos do eletromagnetismo! (pensei no limite extremo).

Faltavam algumas horas para o início da “gran finale” quando dei play em outra partida. Cujo enfrentamento também iria demandar esforço e disposição firme: Como pode força magnética ser responsável por estabelecer força eletromotriz se força magnética nunca fornece energia?

Imediatamente fui tomado por um embaraço teórico. Daqueles que veem quando a gente acha que não entendeu nada, que tudo é complicado, e que nunca vai entender. A primeira reação foi: Vou deixar esse assunto de lado, hoje não é dia pra gente pensar em Física, vou me preparar para o jogo. Comprar algumas “cervejinhas?” Não posso, meu médico me proibiu por causa da diabetes. Buscar uma “carninha?” Sair de casa está complicado, o coronavírus tem avançado em Roraima. As opções eram muito poucas: ficar sentado em frente ao computador olhando aquelas fórmulas ou sonhar com outras coisas. Me deu vontade de fazer outras coisas. Talvez na natureza, em um sítio do interior, perto de um rio ou lago, ou num campo distante, junto de animais selvagens, ou quem sabe, viajando pelo mar afora. Pensei em me mudar para um lugar onde não mais travaria dispustas com a “Physiké,” poderia, até, estar em contato íntimo com a Natureza, quem sabe, olhando com um telescópio as entranhas do Universo, onde até o silêncio não faz barulho, mas me veio a vontade de apenas olhar e contemplar sem explicar.

Quando o sangue do Sanguini baixou, me lembrei que já faz um bocado de tempo que estudo Física. E que as coisas podem ter solução. Mesmo as mais complicadas podem ser esvaziadas das coisas que as complicam. Tudo é questão de tempo, de não desistir \(-\) quando parece que as circunstâncias estão dizendo para você desistir!

Tentei lembrar dos assuntos relacionados com o problema. Escavei à procura do conhecimento enraizado e adormecido. Decidi que iria usar \(-\) em larga escala \(-\) o conhecimento adquirido e algo mais. Pensei: Vou deixar em segundo plano aquilo que li. Vou usar minha receita teórica e dar sabor ao paladar com intuição, lógica e imaginação. Isso mesmo! Vou usar o principal ingrediente do cardápio da resolução de problemas: A intuição! Será um desafio. Não sei se vai ser longo. Espero acabar antes do jogo começar, mas se não der tempo, que boa parte esteja encaminhada.

Comecei a elaborar uma sequência de pensamentos. O que devo atacar? Não a mim mesmo, mas o problema. Tenho uma barra metálica que se move em um campo magnético. Pois bem. Quais são as peças desse problema?

Peça 1: A BARRA METÁLICA. Vou imaginar uma barra de metal de comprimento \(L\).

Peça 2: OS ELÉTRONS. Sim, há muitos elétrons dentro do metal, livres para iniciar um movimento para onde quer que um agente lhes indique a direção.

Peça 3: O CAMPO MAGNÉTICO. De onde vem, para onde vai, como vou imaginar esse campo? Bem, vou imaginar o campo saindo do telhado de minha casa \(-\) é, do telhado \(-\), descendo através do quarto e atravessando a mesa onde está meu notebook \(-\) é, essa mesa que apoia meu notebook \(-\), e se perdendo pelo chão \(-\) sim, pelo chão da minha casa. De cima pra baixo, eis a direção e o sentido que serão adotados neste problema. Além do mais, vou imaginar esse campo não variando com a posição e com o tempo, isso mesmo, pensei, vou imaginar o campo magnético sempre igual em qualquer lugar de minha casa e em qualquer instante em que alguém “olhar para ele.”

Peça 4: A VELOCIDADE. Como vou visualizar a velocidade da barra? Como todo mundo, na certa, imaginaria! A barra passa pelos meus olhos, em um movimento da esquerda para a direita. Sim, é isso mesmo, a barra sai da região da parede esquerda e vai para a região da parede direita, deslizando sobre a mesa (visualizei). Na minha mente, a experiência estava tomando forma. Mas ainda estava faltando alguns detalhes: Definir como a barra iria adquirir velocidade. Ok, o que vou fazer é considerar que ela já possui velocidade quando entra no campo magnético (arquitetei). E a justificativa para isso está no objetivo do estudo: Estudar o que acontece com uma barra e com os elétrons dessa barra quando estão se movendo em uma região em que há um campo magnético aplicado. Nesse sentido, vou imaginar que a barra entra na região do campo com certa velocidade. Pode ser que ela desceu uma rampa (origem: energia potencial gravitacional), ou foi expelida por uma mola (origem: energia potencial elástica). Há muitas maneiras de se fazer isso. O importante, para o problema, é que a barra tenha velocidade dentro do campo magnético. Campos são fascinados por velocidade (pensei). E essa velocidade poderia até ser estimada! Sim, tive a brilante ideia de filmar a experiência. Mas como? Como todo mundo faria! Fixando um celular em um suporte em cima da mesa. E o que o vídeo mostraria? A barra entrando pelo lado esquerdo da tela e saindo pelo lado direito. Contando os frames, e sabendo o valor temporal de cada frame, seria possível estimar a velocidade da barra.

Peça 5: NÃO HÁ ATRITO. Vou eliminar qualquer coisa que “atrapalhe” o movimento da barra: o atrido com a mesa, com o ar, e qualquer outro que alguém poderia se lembrar. Também serão eliminados atritos dos elétrons dentro da barra, choques e espalhamentos com núcleos atômicos, com outros elétrons, com vacâncias ou impurezas \(-\) e qualquer outro evento ainda não descoberto!

2 A calmaria

As peças do problema já foram identificadas e posicionadas para serem manipuladas, agora, há necessidade de juntá-las levando em conta os encaixes da natureza (pensei).

A partir deste ponto, o processo mental será intenso e dinâmico, mas, ao mesmo tempo, apaziguador, pois as nuvens que bloqueiam o entendimento serão afastadas (pensei).

A minha intenção é seguir o elétron e ver o que se passa com ele (mentalizei).

\(-\) Acho que você também deveria seguir essa minúscula partícula e exercitar sua imaginação. Vamos começar?

O elétron cruza um campo magnético dentro de uma barra que se move com certa velocidade para a direita. Fora do campo, o elétron se movimenta exclusivamente para a direita, não há motivo para se dirigir para outro lugar. Mas, e agora, o que acontesse quando ele entra no campo? Precisamos entender o que se passa com uma carga \((q)\) em movimento \((\vec{v})\) quando há um campo magnético \((\vec{B})\) sobre ela.

No espaço vazio, o campo magnético não gera força alguma, pois o seu campo de ação está desprovido de elementos interativos. Para ser fonte de força, há necessita de seu campo de ação ser invadido por uma carga em movimento. No espaço compartilhado, o campo magnético faz surgir uma força sobre a carga:

\[ \vec{F} = q \left( \vec{v} \times \vec{B} \right) . \tag{2.1} \]

No caso deste problema, \(\vec{v}\) é “para a direita,” \(\vec{B}\) é “para baixo,” e \(q = -e\) (negativo, do valor absoluto da carga do elétron, \(e = 1.602 \times 10^{-19}\) C). Dito isso, a força sobre o elétron tem valor absoluto \(evB\), ou a força por unidade de carga é \(vB\).

Segundo (2.1), o sentido da força é determinado pelo sentido de \(\vec{v}\), produto vetorial, sentido de \(\vec{B}\), no caso desta análise, “direita,” produto vetorial, “para baixo.” O resultado aponta “para frente.” Para chegar a essa conclusão, usei minha mão direita. Vou fazer a conta novamente junto com vocês. Acabo de apontar meus dedos no sentido da velocidade, agora estou munhecando na direção do campo, o que vejo? Vejo meu polegar apontar para a parede logo ali, “na minha frente.” Concluo, então, que o produto vetorial é “para frente.”

Mas ainda falta analisar o sinal da carga que aparece na fórmula (2.1). A carga do elétron é negativa, por isso, o sentido da força é contrário de “para frente.” Como vejo meu polegar apontando “para frente,” devo concluir que a força sobre o elétron aponta “em minha direção.”

COMPONENTE 1:

Caminhando para a direita em um campo magnético para baixo, o elétron sofre a ação de uma força em minha direção \((evB)\) .

Agora vamos ter que aumentar a dinâmica do processo mental, pois uma nova entidade acaba de aparecer no problema: A velocidade \(\vec{w}\) que aponta “em minha direção.” É fácil concluir que há uma nova velocidade, pois, a força “em minha direção” acelera o elétron “em minha direção.” É necessário analisar essa nova componente do problema a luz do campo como fonte de força:

\[ \vec{F} = q \left( \vec{w} \times \vec{B} \right) , \tag{2.2} \]

quer dizer, sentido de \(\vec{w}\), produto vetorial, sentido de \(\vec{B}\), ou seja, “em minha direção,” produto vetorial, “para baixo,” resultado, “para a direita.” Mas como a carga é negativa, o sentido da força é contrário de “para a direita.”

COMPONENTE 2:

Caminhando em minha direção em um campo magnético para baixo, o elétron sofre a ação de uma força para a esquerda \((ewB)\) .

No instante em que a barra entra no campo de ação do campo magnético, uma força é disparada sobre ela. A força que age sobre a barra é a força magnética. E, como os parágrafos COMPONENTE 1 e COMPONENTE 2 argumentam, a força magnética desse problema pode ser decomposta em 2 componentes:

\[ \vec{F_m} = q \left( (\vec{v}+\vec{w}) \times \vec{B} \right) . \tag{2.3} \]

É natural representar a força magnética em nosso pensamento apontando para o “vértice esquerdo” da mesa: força (2.1), soma vetorial, força (2.2); ou, “em minha direção,” soma vetorial, “para a esquerda.” Percorrendo nosso cérebro, também é espontâneo visualizar a velocidade do elétron apontando para o “vértice direito” da mesa; “para a direita,” soma vetorial, “em minha direção”:

\[ \vec{v_e} = \vec{v} + \vec{w} , \tag{2.4} \]

Além do mais, é instintivo ajustar a imagem em nossa mente para que a força magnética e a velocidade do elétron formem um ângulo de 90 graus entre si \(-\) depois a gente reforça isso (pensei).

Se não houvesse campo magnético, a barra iria deslizar sobre a mesa com velocidade constante, de valor \(v_0\) (peças 4 e 5). Com o campo aplicado sobre a mesa, a velocidade da barra diminui com o tempo. Se torna dependente do tempo, \(v(t)\). Consegue visualizar elétrons empurrando a parede da barra? É importante destacar que não há força externa para a direita, capaz de igualar a ação da componente da força magnética para a esquerda. Então, depois de algum tempo, a barra para sobre a mesa \((v=0)\).

ILUSTRAÇÃO:

Se você quiser fazer uma comparação com situações do dia a dia, pode imaginar que sob a barra se deposita uma camada “gelatinosa,” grudenta, que breca o movimento sobre a mesa. A força magnética trás consigo essa ideia de algo melado, que cola e gruda, alterando o movimento das cargas. Por exemplo, se uma carga livre entra em uma região de certo campo magnético, podemos imagimar a força do campo “grudando” na carga, resultando em um movimento helicoidal: A compomente da velocidade paralela ao campo não é alterada (produto vetorial igual a zero), entretanto, a compomente da velocidade perpendicular ao campo muda de direção (produto vetorial igual a \(qv_{\bot}B\)).

Voltando ao problema, se a velocidade “para a direita” diminui com o tempo, \(v(t)\), a componente da força magnética “em minha direção” também diminui com o tempo, \(ev(t)B\), consequentemente, a velocidade “em minha direção” diminui com o tempo, \(w(t)\). Por fim, se a velocidade “em minha direção” diminui com o tempo, a componente da força magnética “para a esquerda” também diminui com o tempo, \(ew(t)B\).

O PROBLEMA ESTÁ RESOLVIDO: O entendimento mental está em equilíbrio com o entendimento universal (pensei).

3 Navegando pelo nevoeiro

Até o momento foram utilizadas 4 grandezas na resolução do problema: força, velocidade, campo magnético e carga elétrica. Elas estão interligadas pela equação (2.1).

O nevoeiro conceitual se forma quando se predende analisar outras grandezas relacionadas com o problema. É aqui que aparecem termos como força eletromotriz, trabalho, potencial, diferença de potencial, tensão, potência, entre outros. Já mencionei que estou tentando resolver este problema apoiado na teoria e na intuição e, neste momento, elas me dizem que devo navegar com segurança utilizando a segunda lei de Newton. (Em que cenário?)

O cenário é sobre um elétron em contato com a parede esquerda da barra; não é sobre elétrons que possuem espaço para se moverem em várias direções (como os elétrons localizados na região central da barra); é sobre um elétron que empurra a parede da barra e, ao mesmo tempo, desliza perfeitamente sobre ela; como se a parede fosse feita de um material completamente liso (peça 5), que não oferecesse oposição alguma ao movimento causado pela força “em minha direção,” de valor absoluto \(evB\). Nesse cenário, qual é o papel da parede? Reagir com uma força para a direita. A parede sofre a ação de uma força para a esquerda, causada pelo elétron, de valor absoluto \(ewB\); o elétron sofre a ação de uma força para a direita, causada pela parede, também de valor absoluto \(ewB\); lei de ação e reação de Newton; há duas forças que se cancelam; a força \(ewB\) para a esquerda (reação da parede) e a força \(ewB\) para a direita (ação magnética). Dito isso, quero escrever a segunda lei de Newton para o elétron de massa \(m\) e velocidade \(w\) que desliza pela parede da barra pela ação da força \(evB\) que aponta “em minha direção”:

\[ m \dot{w} = evB . \tag{3.1} \]

Ao escrever o parágrafo acima, estava pensando no seguinte cenário:

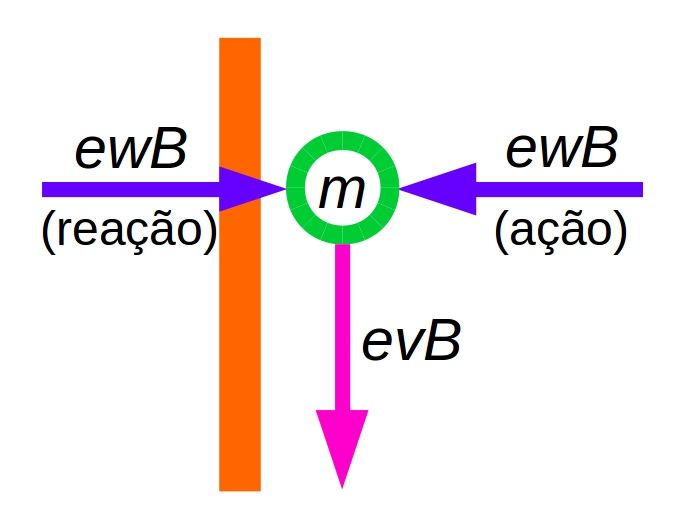
Figura 3.1: Forças que atuam no elétron que desliza pela parede esquerda da barra.

A solução da equação (3.1) depende da velocidade da barra, \(v(t)\). Não sabemos sua expressão, entretanto, é razoável pensar que:

A velocidade da barra inicia com \(v_{0}\), diminui com o tempo, e termina tendendo a zero.

Com essas características, a velocidade da barra pode ter a forma de uma exponencial decrescente:

\[ \bbox[lightgreen, 12px] { v(t) = v_{0} e^{-bt} } \tag{3.2} \]

A substituição da hipótese (3.2) na equação diferencial (3.1) resulta em:

\[ \dot{w} = \frac{eB}{m} v_{0} e^{-bt} . \tag{3.3} \]

Agora podemos fazer a integração temporal:

\[ w = \frac{eB}{m} v_{0} \int e^{-bt} dt , \tag{3.4} \]

com a mudança de variável:

\[ x = -bt \implies dt = -\frac{1}{b}dx \implies w = -\frac{eB}{mb} v_{0} \int e^{x} dx . \tag{3.5} \]

Resultado:

\[ w = -\frac{eB}{mb} v_{0} \left( e^{x} + C \right) \implies w(t) = -\frac{eB}{mb} v_{0} \left( e^{-bt} + C \right) . \tag{3.6} \]

A constante \(C\) é determinada pelas condições iniciais do problema. A velocidade inicial do elétron “em minha direção” é zero, então, basta substituir \(w(0)=0\), na equação acima, o que implica em \(C=-1\). Por fim, a velocidade do elétron é:

\[ \bbox[lightgreen, 12px] { w(t) = \frac{eB}{mb} v_{0} \left[ 1 - e^{-bt} \right] } \tag{3.7} \]

Parece um resultado coerente:

A velocidade do elétron inicia com zero, cresce com o tempo, e tende a um valor terminal.

Se fosse lançado um desafio de resumir esta seção em uma linha, escreveria:

Ocorreu transferência de velocidade: barra \(\longmapsto\) elétron.

E se fosse lançado um desafio de resumir esta seção em uma figura, desenharia:

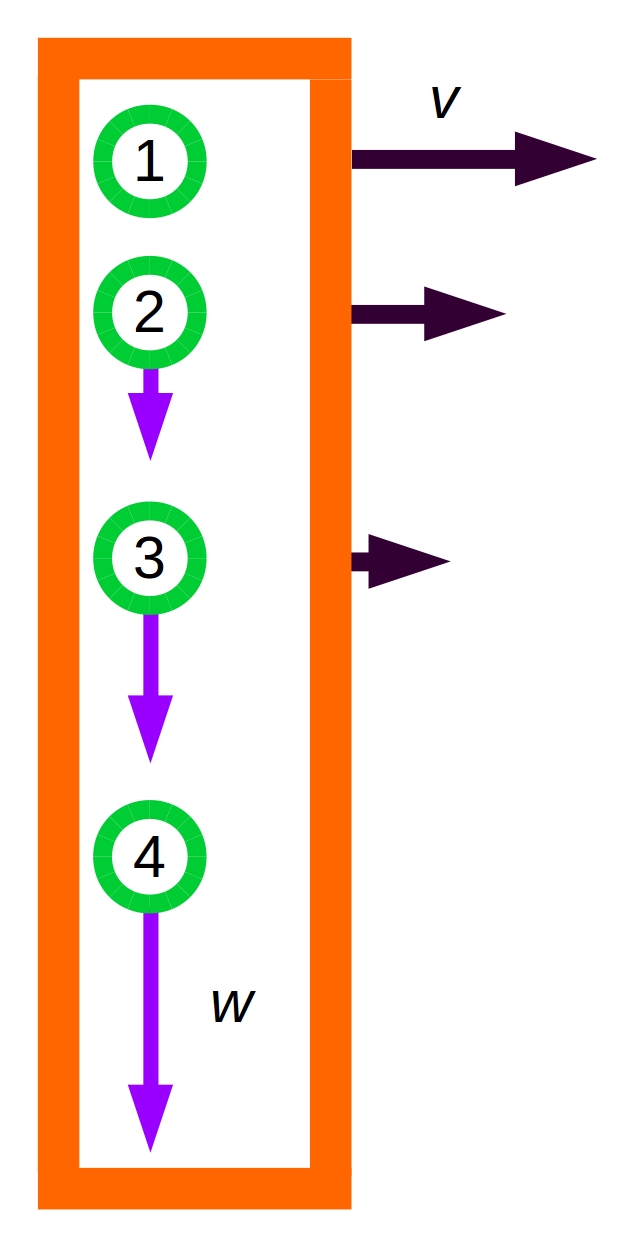
Figura 3.2: Velocidade da barra \(v(t)\) e do elétron \(w(t)\) em 4 instantes de tempo.

No tempo 1 do desenho acima, a barra ainda não chegou à região do campo. Ela desenvolve velocidade “para a direita,” de valor absoluto \(v_{0}\). Nos tempo 2 e 3, o elétron está sob influência do campo magnético. Enquanto a velocidade da barra diminui de valor, a velocidade do elétron aumenta. Depois do tempo 4, a barra está parada sobre a mesa e o elétron continua com velocidade “em minha direção.” É lógico pensar que o elétron vai atingir a região inferior da barra em algum momento. Expandindo esse pensamento, pode-se deduzir que a base inferior vai ficar com acúmulo de elétrons (carga negativa) e que a superior vai ficar com acúmulo de “ausência de elétrons,” quer dizer, com acúmulo de carga positiva.

Qual é o dispositivo que contém um terminal positivo e outro negativo? Na maioria das vezes que falamos sobre bateria, pensamos nas fabricadas com elementos químicos, por exemplo, zinco, lítio, etc. Mas um metal se movendo em um campo magnético também se comporta como uma bateria com polaridades \((+)\) e \((-)\).

A função de uma bateria é transferir energia para as cargas para que se acumulem em terminais. Cada bateria é caracterizada por sua habilidade em separar cargas. A grandeza que mede essa habilidade é a força eletromotriz (fem ou \(\varepsilon\)). Quanto maior for o valor da fem, maior será o acúmulo de cargas nos terminais da bateria. A força eletromotriz não é uma força como as forças de Newton. Nas passagens abaixo, veremos sua relação com energia transferida por unidade de carga.

No geral, a transferência de energia elementar é determinada pela força, produto escalar, deslocamento elementar: \(\vec{F} \cdot d\vec{\ell}\) . A transferência de energia elementar por unidade de carga, então, é determinada pela força por unidade de carga \(\left( \vec{f}=\frac{\vec{F}}{q} \right)\), produto escalar, deslocamento elementar: \(\vec{f} \cdot d\vec{\ell}\). Dito isso, a transferência energia por unidade de carga é:

\[ \bbox[lightgreen, 12px] { \int \vec{f} \cdot d\vec{\ell} } \tag{3.8} \]

Se vamos ficar perdidos no nevoeiro ou se vamos navegar em segurança, depende de sabermos manipular e interpretar essa fórmula: Identificar a força \(\vec{f}\) e o elemento de percurso \(d\vec{\ell}\) e saber fazer a integral. Além disso, analisar a situação em vamos aplicá-la, pois, essa mesma fórmula, pode ser utilizada para se determinar o trabalho feito por unidade de carga \(\left( \frac{W}{q} \right)\) ou a força eletromotriz do dispositivo \((\varepsilon)\) .

São detalhes pouco perceptíveis que precisam ser entendidos com clareza. Por isso, vou chamar o elemento de percurso pelos nomes de retrato e filme, \(d\vec{\ell}_{\rm retrato}\) e \(d\vec{\ell}_{\rm filme}\). A escolha do nome “retrato,” como o nome sugere, significa que vamos tirar uma foto da experência. O que vemos ver na foto? A barra estática e dentro dela podemos imaginar os elétrons se movendo “em minha direção,” traçando \(d\vec{\ell}_{\rm retrato}\) “em minha direção.” Por outro lado, “filme,” como você já concluiu, significa que vamos filmar a experiência. O que vamos ver no vídeo? A barra correndo “para a direita” e, ao mesmo tempo, os elétrons correndo “em minha direção,” e, se tivermos uma mente criativa, vamos assistir os elétrons correndo para o “vértice direito” da mesa, traçando \(d\vec{\ell}_{\rm filme}\) na direção do “vértice direito.”

\(-\) Vamos tentar enchergar melhor nesse nevoeiro. Acho que chegou a hora de orientar a mesa. Fiz um desenho mostrando ela pelo alto e coloquei os eixos cartezianos apropriados para resolver esse problema, ver a Figura 3.3.

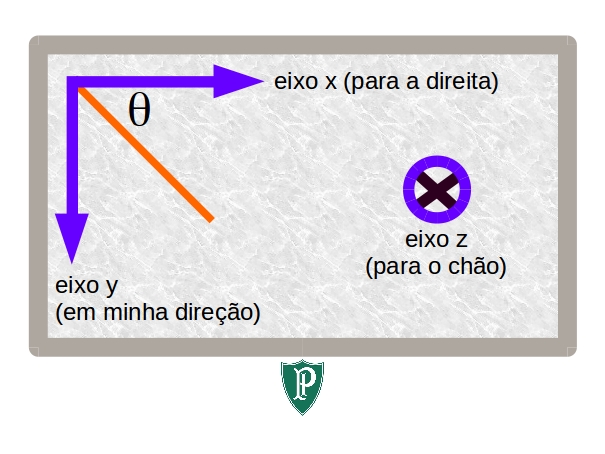
Figura 3.3: Orientação dos eixos cartezianos.

Com base na figura acima:

\[ \begin{aligned} d\vec{\ell}_{\rm retrato} &= dy \,\hat{y} ,\\ d\vec{\ell}_{\rm filme} &= dx \,\hat{x} + dy \,\hat{y} \\ &= d\ell \cos \theta \,\hat{x} + d\ell \sin \theta \,\hat{y} . \end{aligned} \tag{3.9} \]

Com base na figura acima e nos parágrafos COMPONENTE 1 e COMPONENTE 2, pode-se escrever a força magnética por unidade de carga como \((\) \(v = v_e \cos \theta\), \(w = v_e \sin \theta\) \()\):

\[ \begin{aligned} \vec{f} _{m} &= - wB \,\hat{x} + vB \,\hat{y} \\ &= - v_e \sin \theta B \,\hat{x} + v_e \cos \theta B \,\hat{y} . \end{aligned} \tag{3.10} \]

Então, os produtos vetoriais da força magnética com os elementos de percurso são:

\[ \begin{aligned} \vec{f} _{m} \cdot d\vec{\ell}_{\rm retrato} &= vB\, dy ,\\ \vec{f} _{m} \cdot d\vec{\ell}_{\rm filme} &= - v_e \sin \theta B\, d\ell \cos \theta + v_e \cos \theta B\, d\ell \sin \theta = 0 . \end{aligned} \tag{3.11} \]

Você já deve ter lido em algum lugar que a força magnética não realiza trabalho (não transfere energia). E é assim mesmo, sua linha de ação é perpendicular ao deslocamento (reforçando, forma um ângulo de 90 graus com a velocidade). A fórmula (3.8), quando utilizada no “modo filme,” resulta no trabalho feito pela força magnética por unidade de carga, e o valor desse trabalho, é zero. E que dizer da mesma fórmula no “modo retrato?” Neste problema, temos um valor completamente diferente:

\[ \int v(t)\, B\, dy . \tag{3.12} \]

Vamos lançar algumas perguntas para tentar interpretar a equação acima, o resultado dessa integral é:

\(\bullet\) A energia transferida ao elétron?

\(\bullet\) A energia transferida por unidade de carga ao elétron?

\(\bullet\) O trabalho feito pela força magnética por unidade de carga?

\(\bullet\) A força eletromotriz gerada pela barra?

\(\bullet\) A tensão elétrica nos terminais da barra?

\(\bullet\) A diferença de potencial nos terminais da barra?

\(\bullet\) Expresso em joule?

\(\bullet\) Expresso em volt?

Vamos começar pela unidade da integral (3.12) . Se fosse integral de \(\vec{F} \cdot d\vec{\ell}\), o valor seria em joule (J), mas como é \(\frac{\vec{F}}{q} \cdot d\vec{\ell}\), o valor é em volt (V).

Agora vamos interpretar o resultado. Não se trata de energia transferida (J), mas de energia transferida por unidade de carga (V). Esta transferência é causada pela componente da força magnética na direção da barra, não pela força magnética como um todo (força magnética não realiza trabalho). Por isso, (3.12) não deve ser interpretada como um trabalho por unidade de carga, feito pela força magnética por unidade de carga. Então, o que é mais apropriado? É endender (3.12) como um caso típico de utilização da fórmula (3.8) para obtenção da força eletromotriz. E, como este dispositivo tem comprimento \(L\):

\[ \varepsilon = \int _{0} ^{L} v(t)\, B\, dy . \tag{3.13} \]

A tensão elétrica e a diferença de potencial (ddp) são termos equivalentes. Em uma bateria real, o atrito interno (resistência interna) transforma energia útil em forma de calor. Assim, a tensão ou ddp medida nos terminais da bateria é diferente da fem produzida. Todavia, a peça 5 estabelece que não há atrito dentro da barra (resistência interna igual a zero). Por isso, pode-se dizer que a tensão ou ddp nos terminais deste dispositivo ideal tem o mesmo valor numérico da fem (3.13).

A ORIGEM DA ENERGIA CINÉTICA:

A causa determinante da energia cinética da barra foi discutida na peça 4. E sobre a energia cinética dos elétrons:

\(\bullet\) Vem do campo magnético?

\(\bullet\) Vem da barra?

As equações (3.2) e (3.7) deixam claro que a velocidade da barra e a velocidade dos elétrons estão interligadas. O aumento da energia cinética dos elétrons e decorrente da diminuição da energia cinética da barra. A energia cinética dos elétrons é fornecida pela barra. Não é fornecida pelo campo magnético. Então…

\(\bullet\) Qual é o papel do campo magnético?

A atuação do campo se compara às pontes das cidades. Uma ponte não fornece energia. Interligar pontos não acessíveis. Na ausência de campo, a energia cinética da barra fica inacessível aos elétrons. O campo faz a conexão. Como uma ponte, possibilita que a energia cinética da barra chegue aos elétrons.

4 Considerações finais

O problema da barra metálica que se move em um campo magnético é resolvido matematicamente com clareza, entretanto, quando se procura entendê-lo fisicamente, podem surgir conceitos aparentemente conflitantes \(-\) (Dionisio 2007); (Dionisio 2010); (Mosca 1974).

\(-\) Como pode força magnética ser responsável por estabelecer força eletromotriz se força magnética não realiza trabalho (fornece energia)?

A resposta a esta inquietação foi dada mostrando que uma mesma fómula é utilizada para se determinar trabalho e força eletromotriz. A fórmula (3.8). O ponto central da questão foi entendido separando estes dois conceitos mediante os deslocamentos infinitesimais \(d\vec{\ell}_{\rm retrato}\) e \(d\vec{\ell}_{\rm filme}\).

Figura 4.1: Obrigado pela leitura.

\(-\) É, o problema foi suado, longo, demorado. Não foi possível resolver tudo antes do jogo. Mas, depois, foi mais prazeroso!