1 Introdução

Os físicos chamam a função que representa um elétron confinado em um potencial central de função de onda. Os químicos preferem chamar essa mesma função de orbital.

É importante conhecer as duas linguagens: se expressar através das funções de onda e por meio dos orbitais. Por exemplo, a soma das funções de onda 1√2(ψ21−1−ψ211), sendo:

ψ21−1=1√64π(Za)52re−Zr/2asinθe−iϕ,

ψ211=−1√64π(Za)52re−Zr/2asinθeiϕ,

é o orbital 2px:

2px=1√32π(Za)52re−Zr/2asinθcosϕ.

Já o orbital 2py é a superposição das funções de onda i√2(ψ21−1+ψ211):

2py=1√32π(Za)52re−Zr/2asinθsinϕ.

E, o orbital 2pz é a própria função de onda ψ210, ele não é fruto de superposição:

2pz=1√32π(Za)52re−Zr/2acosθ.

Ademais, as funções de onda ψ211 e ψ21−1 são chamadas de orbitais 2p+1 e 2p−1, respectivamente (Peter Atkins 2011).

No geral, a função de onda é escrita como ψnlm, onde: n é o número quântico principal, l é o momento angular orbital, e m é a projeção do momento angular orbital no eixo z. Assim, as funções de onda ψ211, ψ210 e ψ21−1 possuem n=2, l=1 e projeções m=1,0,−1, respectivamente.

Do ponto de vista dos orbitais, os números l recebem nomes especiais, dados pela convenção de espectroscopia atômica:

l=0⟹s,l=1⟹p,l=2⟹d,l=3⟹f,l=4⟹g,l=5⟹h.

Por isso, os orbitais s são orbitais de momento angular orbital l=0, os orbitais p são orbitais de momento angular orbital l=1, e assim por diante.

Percebe-se que as equações (1.3), (1.4) e (1.5) são funções de três variáveis, pois a distância do elétron ao núcleo depende das coordenadas do elétron em relação ao núcleo:

r=√x2+y2+z2.

Os ângulos θ e ϕ também dependem das coordenadas do elétron em relação ao núcleo:

θ=arccos(z/r),ϕ=arctan(y/x).

O artigo foi escrito com o objetivo de compartilhar a técnica computacional envolvida na visualização de funções com 3 variáveis. Como todos sabem, para se graficar uma função com 3 variáveis necessitaríamos de um espaço com 4 eixos: 3 eixos para as variáveis (x,y,z), e um quarto eixo para se colocar os valores da função f(x,y,z). Fica claro que não há possibilidade de graficar esse tipo de função da mesma maneira que graficamos uma função com 2 variáveis: utilizando 2 eixos para as variáveis (x,y), e um terceiro eixo com o valor da função f(x,y).

No caso das funções com 3 variáveis, deve-se utilizar métodos de visualização volumétrica, os quais criam uma superfície no espaço, de pontos (x,y,z), sendo que, ao percorrer essa superfície, a função f(x,y,z) é uma constante. Em outras palvras, contrói-se uma superfície tridimensional na qual f(x,y,z)=α, sendo α um parâmetro. As superfícies de contorno tridimensionais assim construídas são chamadas isosuperfícies.

Vamos utilizar como método de visualização de isosuperfícies, o algoritmo dos cubos marchando (marching cubes algorithm), desenvolvido por Lorensen e Cline (W E Lorensen 1987). Este algoritmo faz parte do utilitário contour3d, do pacote misc3d, desenvolvido por Feng and Tierney para a linguagem de programação R (Dai Feng 2008).

2 Os elementos de trabalho

Antes de começarmos a fazer os gráficos dos orbitais, vamos entender os elementos de trabalho.

Estudaremos a estrutura eletrônica da molécula de hidrogênio, H2, formada por 2 núcleos de hidrogênio e por 2 elétrons. Os núcleos serão identificados por núcleo a e núcleo b, e os elétrons por elétron 1 e elétron 2.

A Fig. 2.1 mostra a geometria do problema. Os núcleos foram colocados sobre o eixo z e estão separados pela distância R. As distâncias dos elétrons i=1,2 até os núcleos a e b são representadas pelos vetores rai e rbi, de módulos:

rbi=√x2i+y2i+(zi−R)2,rai=√x2i+y2i+z2i.

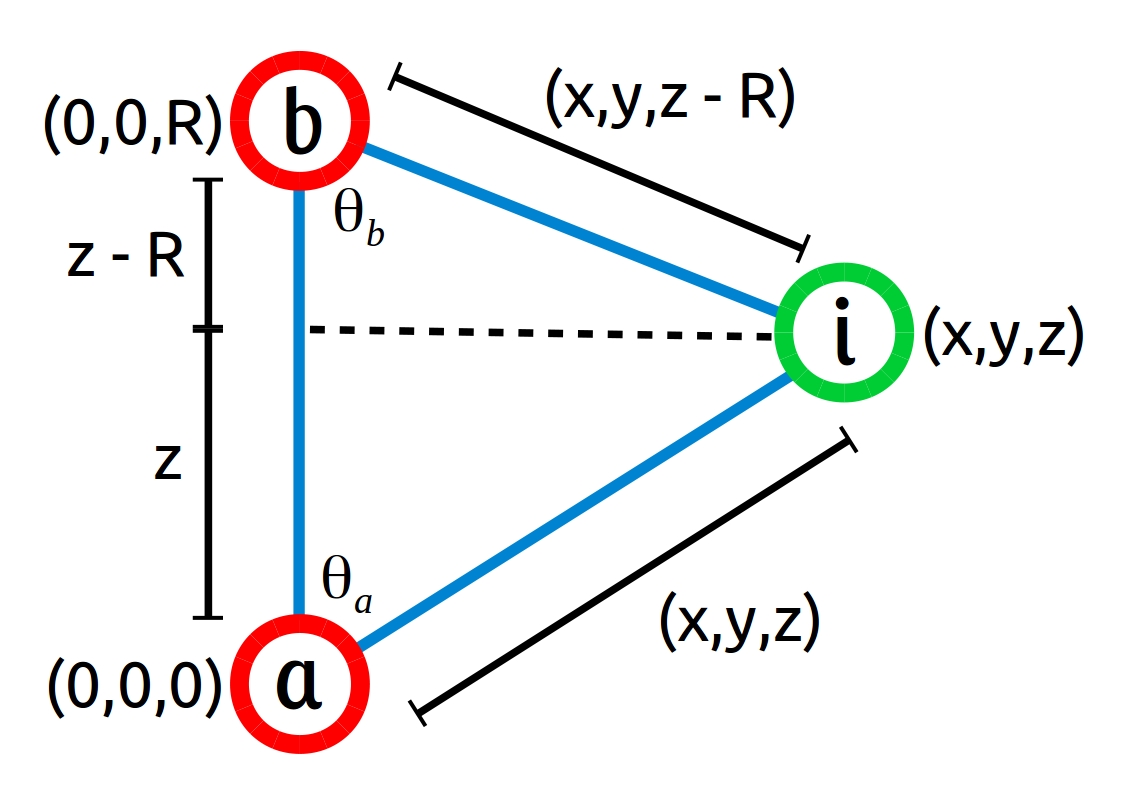
Figura 2.1: Distâncias e ângulos dos elétrons i=1,2 em relação aos núcleos a e b.

Os ângulos que os elétrons i=1,2 fazem com o eixo z, são:

θbi=arccos[(zi−R)/rbi],θai=arccos[zi/rai].

Os ângulos que os elétrons i=1,2 fazem com o eixo x, são:

ϕbi=arctan(yi/xi),ϕai=arctan(yi/xi).

Nota: Os ângulos (2.3) não aparecem na Fig. 2.1.

3 A ocupação de orbitais

O elétron 1 pode ocupar o orbital atômico do núcleo a. Vamos representar essa ocupação dizendo que ψa(1). Se o elétron 1 está no orbital do núcleo a, é possível que o elétron 2 esteja no orbital do núcleo b, então, é possível escrever ψb(2). Esta maneira de ocupar os orbitais dos átomos de hidrogênio proporciona que o orbital da molécula de H2 seja:

Ψ=ψa(1)ψb(2).

Todavia, também é possível que o elétron 2 ocupe o orbital atômico do núcleo a e o elétron 1 ocupe o orbital do núcleo b, então, também é possível escrever ψa(2) e ψb(1), respectivamente. Esta nova configuração viabiliza que o H2 tenha o seguinte orbital molecular:

Ψ=ψa(2)ψb(1).

Visto que (3.1) e (3.2) são igualmente prováveis, o orbital molecular total do H2 deve ser a superposição das funções de onda de cada possibilidade (Peter Atkins 2011):

Ψ=ψa(1)ψb(2)+ψa(2)ψb(1).

Nota: A equação acima não está normalizada.

Vamos entender como utilizar a equação (3.3). A ideia é atribuir orbitais eletrônicos ao redor dos núcleos a e b. Vamos supor que ψa=2pz e que ψb=2pz. Substituindo a fórmula (1.5) em (3.3), e deixando de lado a constante 1√32π(1a)52, tem-se:

Ψ=ra1e−ra1/2acosθa1×rb2e−rb2/2acosθb2+ra2e−ra2/2acosθa2×rb1e−rb1/2acosθb1.

Nota: Como estamos trabalhando com hidrogênios, Z=1.

As distâncias são determinadas pelas fórmulas (2.1):

ra1=√x21+y21+z21,rb2=√x22+y22+(z2−R)2,ra2=√x22+y22+z22,rb1=√x21+y21+(z1−R)2.

Já os ângulos são calculados pelas equações (2.2):

θa1=arccos[z1/ra1],θb2=arccos[(z2−R)/rb2],θa2=arccos[z2/ra2],θb1=arccos[(z1−R)/rb1].

4 O código fonte

Estamos com as ferramentas necessárias para dar início à escrita do código que vai gerar os gráficos das isosuperfícies.

A ideia central é fazer uma malha de pontos (x,y,z) com três comandos seq(-10,10,length=101), para alimentar as fórmulas dos orbitais. Depois, escrever uma função com o comando function() que vai conter as fórmulas dos orbitais e, em seguida, chamar o comando contour3d que se encarregará de fazer as isosuperfícies.

#Construção da malha espacial de pontos
x <- seq(-17,18,length=101)
y <- seq(-16,19,length=101)
z <- seq(-15,20,length=101)

 #Função que contém as fórmulas dos orbitais
 OrbMO <- function(x,y,z) {
       x1 <- x
       y1 <- y
       z1 <- z
       R  <- 1.4
       r_b1 <- sqrt(x1^2 + y1^2 + (z1-R)^2)
       theta_b1 <- acos( (z1-R)/r_b1 )
       phi_b1   <- atan2(y1,x1)

       x2 <- x
       y2 <- y
       z2 <- z
       r_b2 <- sqrt(x2^2 + y2^2 + (z2-R)^2)
       theta_b2 <- acos( (z2-R)/r_b2 )
       phi_b2   <- atan2(y2,x2)

       r_a1     <- sqrt(x1^2 + y1^2 + z1^2)
       theta_a1 <- acos(z1/r_a1)
       phi_a1   <- atan2(y1, x1)

       r_a2     <- sqrt(x2^2 + y2^2 + z2^2)
       theta_a2 <- acos(z2/r_a2)
       phi_a2   <- atan2(y2, x2)

  b1 <-                                    exp(-r_b1  ) /sqrt(   pi) #1s
  b2 <-                                    exp(-r_b2  ) /sqrt(   pi) #1s       
  a1 <-                                    exp(-r_a1  ) /sqrt(   pi) #1s       
  a2 <-                                    exp(-r_a2  ) /sqrt(   pi) #1s       

  b1 <- (2 - r_b1)                       * exp(-r_b1/2) /sqrt(32*pi) #2s
  b2 <- (2 - r_b2)                       * exp(-r_b2/2) /sqrt(32*pi) #2s
  a1 <- (2 - r_a1)                       * exp(-r_a1/2) /sqrt(32*pi) #2s
  a2 <- (2 - r_a2)                       * exp(-r_a2/2) /sqrt(32*pi) #2s

  b1 <- cos(theta_b1)             * r_b1 * exp(-r_b1/2) /sqrt(32*pi) #2pz
  b2 <- cos(theta_b2)             * r_b2 * exp(-r_b2/2) /sqrt(32*pi) #2pz      
  a1 <- cos(theta_a1)             * r_a1 * exp(-r_a1/2) /sqrt(32*pi) #2pz      
  a2 <- cos(theta_a2)             * r_a2 * exp(-r_a2/2) /sqrt(32*pi) #2pz      

  b1 <- sin(theta_b1)*cos(phi_b1) * r_b1 * exp(-r_b1/2) /sqrt(32*pi) #2px
  b2 <- sin(theta_b2)*cos(phi_b2) * r_b2 * exp(-r_b2/2) /sqrt(32*pi) #2px
  a1 <- sin(theta_a1)*cos(phi_a1) * r_a1 * exp(-r_a1/2) /sqrt(32*pi) #2px
  a2 <- sin(theta_a2)*cos(phi_a2) * r_a2 * exp(-r_a2/2) /sqrt(32*pi) #2px

  a1                   #Fórmula do orbital atômico
  a1 * b2  +  a2 * b1  #Fórmula do orbital molecular
  }

contour3d(OrbMO, x,y,z, level=0.001) #Construção da isosuperfície

O programa é bem flexível, pode-se comentar linhas para gerar isosuperfícies das mais variadas: observe que há o bloco do orbital 1s, 2s, 2pz e 2px. Lembrando que em R, os comentários são feitos com #. Há duas opções de gráficos: (1) pode-se graficar o orbital atômico, deixando a linha a1 ativa; ou (2) pode-se graficar o orbital molecular, deixando a linha a1*b2+a2*b1 ativa. É o vamos fazer a partir de agora.

5 Os orbitais atômicos

Para graficar os orbitais atômicos, deve-se comentar a linha a1*b2+a2*b1. Ademais, deve-se deixar ativo apenas o bloco do orbital que se deseja graficar. Por exemplo, para graficar o orbital atômico 1s, deve-se comentar os blocos 2s, 2pz, 2px (colocando # na frente de cada linha).

As figuras 5.1, 5.2, 5.3 e 5.4, apresentam os orbitais atômicos 1s, 2s, 2pz e 2px do hidrogênio, respectivamente.

Por causa da fórmula do orbital 2s apresentar o termo (2−r), seu gráfico mostra duas cascas, enquanto que o gráfico do orbital 1s apresenta somente uma.

Na visualização dos orbitais 2pz e 2px, foi utilizada a técnica de disparar várias isosuperfícies concentrícas. Isso é feito atribuindo valores à opção level do comando contour3d. Como o máximo e o mínimo desses orbitais ocorrem entre (−0,07 e 0,07), foi escolhido os seguintes valores:

cut <- c(-0.06, -0.04, -0.02, 0.02, 0.04, 0.06)
contour3d(OrbMO, x,y,z, level=cut)

Nota: Confira no artigo (Dai Feng 2008) mais exemplos de como utilizar o pacote misc3d e seu poderoso comando contour3d.

Fica claro que o orbital 2pz aponta para o eixo z, e o 2px para o eixo x.

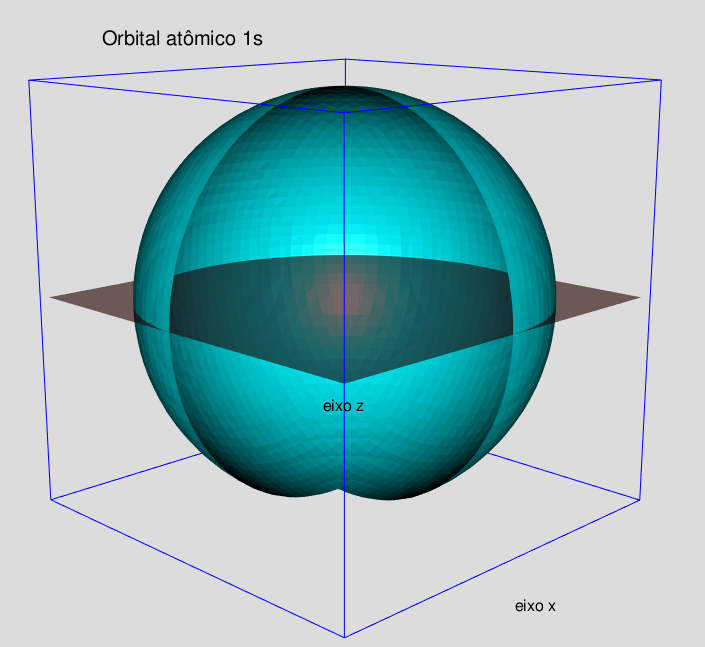
Figura 5.1: Núcleo de hidrogênio exibindo orbital 1s.

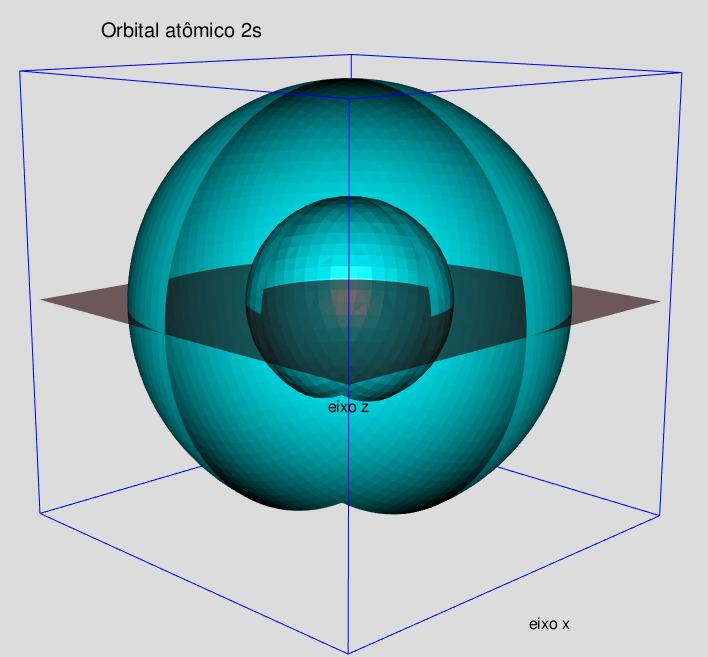
Figura 5.2: Núcleo de hidrogênio exibindo orbital 2s.

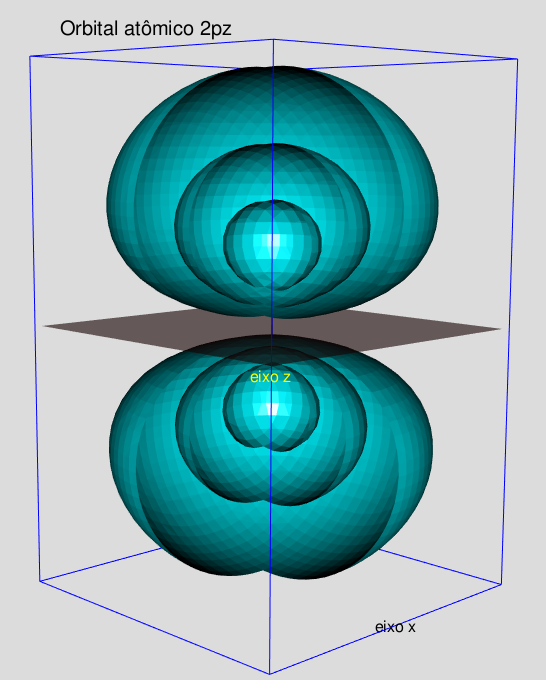
Figura 5.3: Núcleo de hidrogênio exibindo orbital 2pz: 3 isosuperfícies.

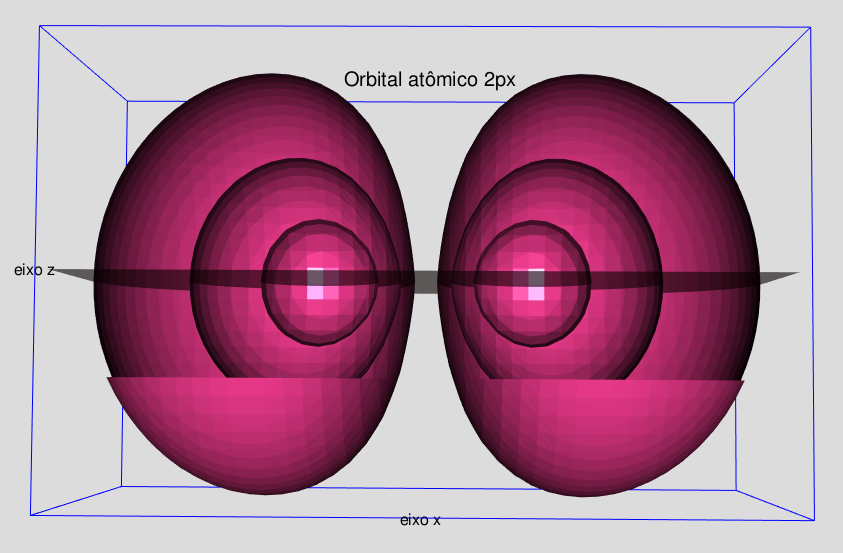
Figura 5.4: Núcleo de hidrogênio exibindo orbital 2px: 3 isosuperfícies.

6 Os orbitais moleculares

Agora, para graficar os orbitais moleculares, deve-se comentar a linha a1. Ademais, deve-se novamente deixar ativo apenas o bloco do orbital que se deseja graficar.

O valor experimental da distância entre os núcleos a e b, da molécula de hidrogênio, é R=1,40 a0, segundo (Peter Atkins 2011).

Nota: Os orbitais estão sendo graficados ajustando a0=1 para efeito de simplificação.

As figuras 6.1, 6.2, 6.3 e 6.4, apresentam os orbitais moleculares da molécula de hidrogênio, com os núcleos a e b exibindo: ambos 1s (1s1s); ambos 2s (2s2s); ambos 2pz (2pz2pz); e ambos 2px (2px2px).

Nota: Os casos 2pz2pz e 2px2px apresentam 3 isosuperfícies concentrícas.

Planos cortando a localização dos núcleos também foram graficados: para o núcleo a, o plano é (x,y,0), e para o núcleo b, (x,y,R). Os comandos para graficar os planos são:

planes3d(0,0,1, d=-1.4, col="red", alpha=0.6) #Plano sobre o núcleo "b"
planes3d(0,0,1, d= 0.0, col="red", alpha=0.6) #Plano sobre o núcleo "a"

O orbital molecular do caso 1s1s apresenta apenas 1 casca, enquanto que o do caso 2s2s, 3 cascas: decorrente da multiplicação de termos (2−ra) e (2−rb).

A ligação efetuada pelo orbital molecular 2pz2pz é predominantemente na direção do eixo z, enquando que a do 2px2px é na direção do eixo x.

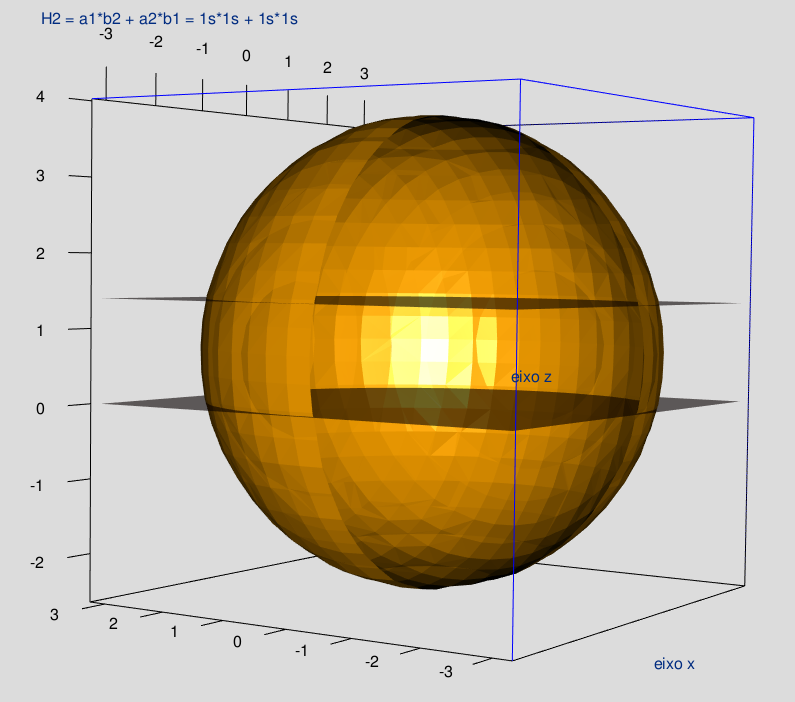
Figura 6.1: H2: Núcleos a e b na configuração 1s1s.

Figura 6.2: H2: Núcleos a e b na configuração 2s2s.

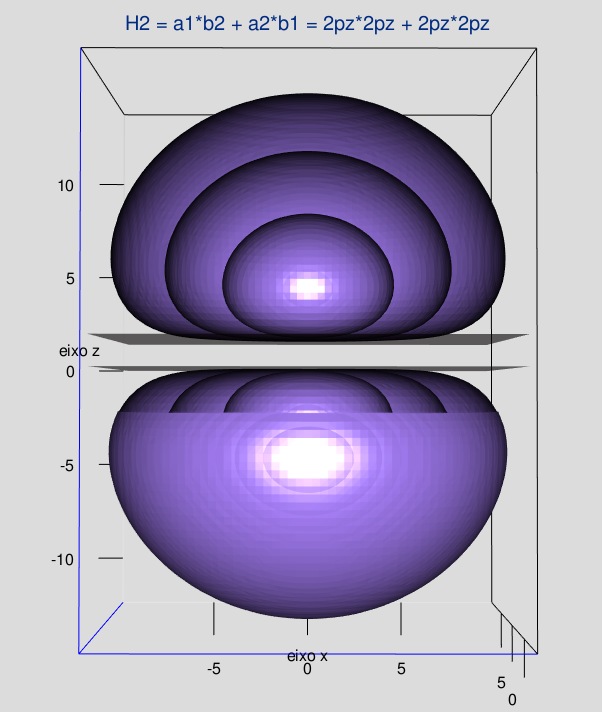
Figura 6.3: H2: Núcleos a e b na configuração 2pz2pz: 3 isosuperfícies.

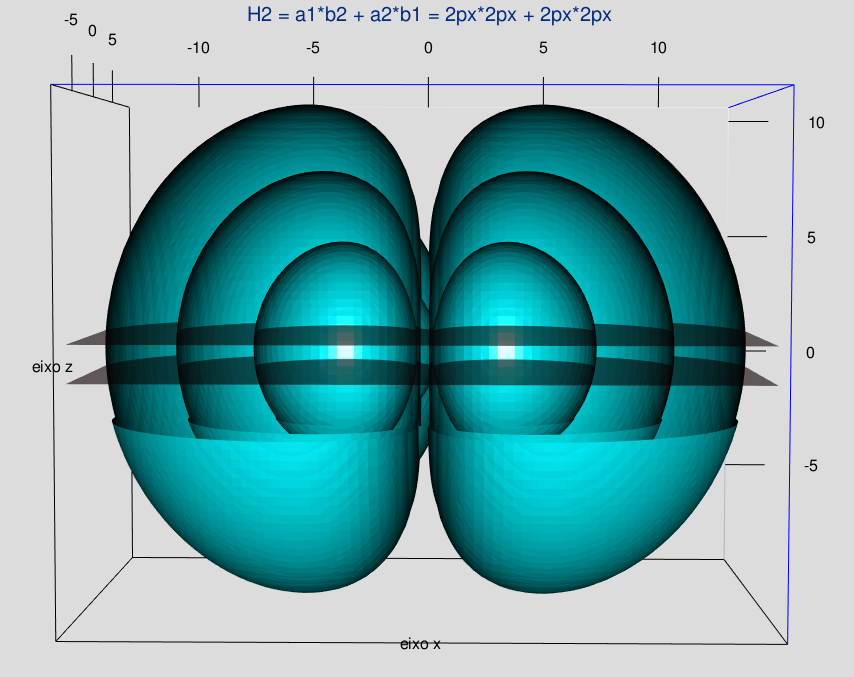
Figura 6.4: H2: Núcleos a e b na configuração 2px2px: 3 isosuperfícies.

Vale ressaltar que, em um ambiente natural, é atípico a molécula de hidrogênio estar excitada a ponto de seus elétrons ocuparem o orbital molecular 2pz2pz, ou 2px2px. É comum que ela se encontre no estado fundamental: quando os 2 elétrons ocupam o orbital molecular 1s1s. Já em um ambiente agitado, a molécula de hidrogênio pode ir para o primeiro estado excitado: construído com um elétron ocupando o orbital atômico 1s, e o outro elétron, o 2s, resultando na configuração molecular 1s2s. Este orbital misto também é possível de ser graficado acrescentando o seguinte bloco ao código fonte (ver figura 6.5):

b1 <- (2 - r_b1) * exp(-r_b1/2) /sqrt(32*pi) #2s
b2 <- (2 - r_b2) * exp(-r_b2/2) /sqrt(32*pi) #2s 
a1 <-              exp(-r_a1  ) /sqrt(   pi) #1s    
a2 <-              exp(-r_a2  ) /sqrt(   pi) #1s

Figura 6.5: Molécula de hidrogênio na configuração 1s2s.

7 Conclusão

A visualisação de funções com 3 variáveis é um problema gráfico que exige técnicas computacionais avançadas. Com a pesquisa do artigo (Dai Feng 2008), pude notar que seria possível visualizar orbitais atômicos e moleculares utilizando a linguagem R. O código fonte compartilhado é flexível e pode ser implemantado para outras situações.