1 Introdução
O artigo 2-Massas, 2-Poços; 2-Massas, 1-Poço; 2-Elétrons, 2-Poços; 2-Elétrons, 1-Poço analisa 4 situações de 2-partículas confinadas em poços quânticos.
Este artigo analisa a situação de 1-elétron confinado em 2-poços quânticos. Na literatura, o sistema é conhecido como Double Quantum Well (DQW) — Poço Quântico Duplo. A estrutura é formada por 2-poços separados por 1-barreira delgada, o que permite o tunelamento do elétron através da barreira (Tetsuya Tada 1988). Isso significa que há probabilidade do elétron ser encontrado no primeiro e também no segundo poço do DQW.
Um método – para se determinar a energia de confinamento e a função de onda de um DQW – é o método numérico (A Keshavarz 2010).
Neste artigo – a energia de confinamento e a função de onda – serão encontradas com base em resultados de equações transcendentais (Tsuneo Kamizato 1989). A técnica consiste em cruzar equações que levam em conta condições de continuidade da função de onda nas interfaces poço/barreira — o local do cruzamento pode ser determinado por meio de um gráfico.
2 O perfil do potencial
O poço quântico duplo (DQW) é formado por 2-poços retangulares separados por 1-barreira central. Neste artigo, os poços serão considerados com potencial negativo, V(x)=−V0, e as barreiras laterais e central, com potencial igual a zero, V(x)=0. A Fig. 2.1 mostra o perfil de potencial e a nomenclatura adotada para designar cada peça do DQW.
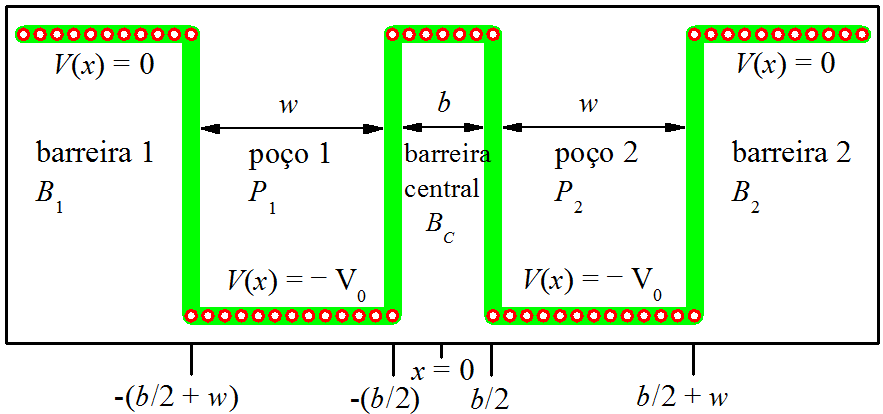
Figura 2.1: Perfil de potencial do poço quântico duplo e nomenclatura das peças.
Olhando os cortes da Fig. 2.1, nota-se que (b,w) representam a largura de barreira central e largura de poço individual, respectivamente. Também, que há simetria em relação à origem das posições (x=0). Por isso, esse tipo de DQW é classificado como simétrico – é classificado como assimétrico quando os poços são diferentes, por exemplo, caso não possuam larguras ou profundidades iguais (J Ram 2006).
3 As características da função de onda
O estudo se concentrará na energia de partícula menor que a altura de barreira e maior que o fundo de poço, ou seja, quando a energia do elétron estiver entre −V0<E<0.
Na região dos poços, o número de onda da peça de função de onda é real:
k=1ℏ√2m(E+V0),
e a solução da equação de Schrödinger resulta em exponencial complexa, do tipo e±ikx.
Na região das barreiras (central, barreira-1 e barreira-2), a combinação de potencial nulo com energia de partícula negativa produz número de onda imaginário:
kimg=1ℏ√2m(E−0),
sendo conveniente escrevê-lo na forma
kimg=iq,
onde
q=1ℏ√2m(0−E).
Então, na região das barreiras, a solução da equação de Schrödinger resulta em exponencial real, do tipo e±qx.
Em (3.1) e (3.4), as grandezas m e ℏ representam a massa do elétron e a constante de Planck, nesta ordem.
Explorar a simetria do DQW 2.1 poupa trabalho na hora de determinar a função de onda global, que se estende de −∞<x<∞, pois, é preciso se preocupar apenas com a determinação da função do lado direito do DQW, já que a função do lado esquerdo (x<0) é mais ou menos igual à função do lado direito (x>0):
Ψ(x<0)=±Ψ(x>0).
Na linguagem matemática, quando
Ψ(x<0)=+Ψ(x>0),
diz-se que a função é par (seu gráfico tem simetria em relação ao eixo vertical), e quando
Ψ(x<0)=−Ψ(x>0),
é dito que a função é ímpar (seu gráfico tem simetria em relação à origem).
Logo, as soluções do DQW 2.1 se dividem em 2-grupos: o conjunto de funções de onda pares e o conjunto de funções de onda ímpares.
Deve-se escolher peças de função de onda com o objetivo de simplificar a manipulação matemática. O capítulo 9 do livro Confinamento e Espalhamento por Potenciais Retangulares, que trata do poço quântico simples, iniciou a análise utilizando peças complexas, todavia, após alguns passos matemáticos, transformou-se as peças complexas em peças reais (senos e cossenos). Neste artigo, vamos prontamente iniciar o estudo considerando soluções reais.
Qual solução poderá compor as peças dos poços?
Há propagação de ondas dentro dos poços, ondas que incidem e refletem na interface poço/barreira, então, poderia-se operar com uma combinação de exponenciais complexas, todavia, é mais conveniente usar uma combinação de seno e cosseno.
Qual solução poderá compor a peça da barreira central?
Não há propagação de ondas na barreira central, a solução é a soma de duas exponenciais reais: as que fariam a vez da “onda incidente” e da “onda refletida” – aqui cabe lembrar que a combinação de exponenciais reais resulta em cosseno hiperbólico ou seno hiperbólico.
Qual solução poderá compor as peças das barreiras laterais?
Também não há propagação de ondas nas barreiras laterais, a solução poderia ser do mesmo tipo da barreira central, a soma de duas exponenciais reais, todavia, as barreiras laterais se estendem até o infinito, por isso, a única exponencial que deve permanecer na solução, é aquela que tende a zero no infinito.
4 A equação da energia
Esta seção apresenta o procedimento que leva à equação capaz de fornecer os valores da energia de confinamento do elétron, uma equação cujas raizes podem ser determinadas com auxílio gráfico, denominada equação transcendental.
A notação que é utilizada para descrever as peças da função de onda global, está impressa na Fig. 2.1.
As ponderações feitas na seção [3] nos leva a concentrar o trabalho ao redor do poço-2.
Com o intuito de utilizar o padrão Latex,
será utilizado sin para seno, cos para cosseno, tan para tangente, exp para exponencial,
cosh para cosseno hiperbólico e sinh para seno hiperbólico.
A função de onda dentro do poço-2 é escrita como combinação de seno e cosseno:
P2(x)=Pcos[kx]+Qsin[kx],
onde P e Q são amplitudes e k é o número de onda (3.1).
A função de onda dentro da barreira-2 tem a forma de uma exponencial que decai em função do número de onda (3.4):
B2(x)=Dexp[−qx].
A função de onda deve ser contínua na interface poço/barreira, para isso, iguala-se (4.1) com (4.2) no ponto x=b/2+w:
Pcos[k(b/2+w)]+Qsin[k(b/2+w)]=Dexp[−q(b/2+w)].
A derivada da função de onda também deve ser contínua na interface poço/barreira, para isso, deriva-se as Eqs. (4.1) e (4.2)
P′2(x)=−kPsin[kx]+kQcos[kx],B′2(x)=−qDexp[−qx],
e, depois, iguala-se os resultados das derivadas no ponto x=b/2+w:
−Psin[k(b/2+w)]+Qcos[k(b/2+w)]=−qkDexp[−q(b/2+w)].
Divide-se a Eq. (4.6) pela Eq. (4.3):
−Psin[k(b/2+w)]+Qcos[k(b/2+w)]Pcos[k(b/2+w)]+Qsin[k(b/2+w)]=−qk.
Manipula-se a Eq. (4.7) até chegar no agrupamento dos senos e os cossenos:
−Qsin[k(b/2+w)][1−kqPQ]=Pcos[k(b/2+w)][1+kqQP].
Encerra-se a dedução utilizando a definição de tangente:
tan[k(b/2+w)]=−(P/Q)[1+(k/q)(Q/P)][1−(k/q)(P/Q)].
Que informação se torna pública por meio da equação transcendental (4.9)?
Disparando o gráfico da Eq. (4.9), a energia de confinamento é determinada fixando atenção no cruzamento que a curva tangente faz com a curva da expressão do lado direito.
Das variáveis da Eq. (4.9), ainda resta saber a expressão de P/Q. Conforme discutido na seção [3], há uma expressão vinculada ao conjunto de funções de onda pares e outra vinculada ao conjunto de funções de onda ímpares.
4.1 A expressão de P/Q
Esta seção determina a expressão de P/Q, vinculada à função de onda par. Para isso, analisa a continuidade da função de onda na interface poço-2/barreira-central: ponto x=b/2.
A função de onda dentro da barreira-central é descrita por um cosseno hiperbólico, já que cossenos hiperbólicos são funções pares:
Bc(x)=Bcosh[qx].
A derivada do cosseno hiperbólico resulta em seno hiperbólico
B′c(x)=qBsinh[qx].
A função de onda deve ser contínua na interface poço/barreira, para isso, iguala-se (4.1) com (4.10) no ponto x=b/2:
Pcos[k(b/2)]+Qsin[k(b/2)]=Bcosh[q(b/2)].
A derivada da função de onda também deve ser contínua na interface poço/barreira, para isso, no ponto x=b/2, iguala-se P′2(x) de (4.4) com B′c(x) de (4.11):
Psin[k(b/2)]−Qcos[k(b/2)]=−qkBsinh[q(b/2)].
Multiplicação da Eq. (4.12) por cos[k(b/2)]:
Pcos2[k(b/2)]+Qsin[k(b/2)]cos[k(b/2)]=Bcosh[q(b/2)]cos[k(b/2)].
Multiplicação da Eq. (4.13) por sin[k(b/2)]:
Psin2[k(b/2)]−Qcos[k(b/2)]sin[k(b/2)]=−qkBsinh[q(b/2)]sin[k(b/2)].
Lembrando que cos2+sin2=1, soma das Eqs. (4.14) e (4.15):
P=Bcosh[q(b/2)]cos[k(b/2)]−qkBsinh[q(b/2)]sin[k(b/2)].
Agora, multiplicação da Eq. (4.12) por sin[k(b/2)], multiplicação da Eq. (4.13) por cos[k(b/2)], e soma dos resultados:
Q=Bcosh[q(b/2)]sin[k(b/2)]+qkBsinh[q(b/2)]cos[k(b/2)].
Por fim, a divisão de (4.16) por (4.17), resulta na expressão de P/Q (função par):
P/Q=(k/q)cosh[q(b/2)]cos[k(b/2)]−sinh[q(b/2)]sin[k(b/2)](k/q)cosh[q(b/2)]sin[k(b/2)]+sinh[q(b/2)]cos[k(b/2)].
4.2 A expressão de ˉP/ˉQ
Esta seção segue o procedimento da seção [4.1] — com algumas adaptações.
A função de onda de caráter ímpar será marcada com uma barra.
A função de onda dentro da barreira-central, agora, é ímpar, por isso, é representada por um seno hiperbólico, já que senos hiperbólicos são funções ímpares:
ˉBc(x)=ˉBsinh[qx],ˉB′c(x)=qˉBcosh[qx].
A função de onda dentro do poço-2 continua escrita como combinação de seno e cosseno:
ˉP2(x)=ˉPcos[kx]+ˉQsin[kx],ˉP′2(x)=−kˉPsin[kx]+kˉQcos[kx].
Semelhante ao que fizemos na seção anterior, é hora de aplicar as condições de continuidade no ponto x=b/2 e manipular os resultados. Com um pouco de trabalho, é fácil mostrar que ˉP/ˉQ (função ímpar) tem o aspecto:
ˉP/ˉQ=(k/q)sinh[q(b/2)]cos[k(b/2)]−cosh[q(b/2)]sin[k(b/2)](k/q)sinh[q(b/2)]sin[k(b/2)]+cosh[q(b/2)]cos[k(b/2)].
5 Determinação da energia de confinamento
A determinação da energia do elétron confinado no poço quântico duplo lança mão da equação transcendental desenvolvida na seção [4] e das equações de apoio elaboradase nas seções [4.1] e [4.2]. Vamos, então, agrupá-las nesta seção.
Equações de função de onda par:
tan[k(b/2+w)]=−(P/Q)[1+(k/q)(Q/P)][1−(k/q)(P/Q)],
P/Q=(k/q)cosh[q(b/2)]cos[k(b/2)]−sinh[q(b/2)]sin[k(b/2)](k/q)cosh[q(b/2)]sin[k(b/2)]+sinh[q(b/2)]cos[k(b/2)].
Equações de função de onda ímpar:
tan[k(b/2+w)]=−(ˉP/ˉQ)[1+(k/q)ˉQ/ˉP][1−(k/q)ˉP/ˉQ],
ˉP/ˉQ=(k/q)sinh[q(b/2)]cos[k(b/2)]−cosh[q(b/2)]sin[k(b/2)](k/q)sinh[q(b/2)]sin[k(b/2)]+cosh[q(b/2)]cos[k(b/2)].
O método requer varredura na energia do elétron, que é negativa, e está embutida nos números de onda:
k=1ℏ√2m(E+V0),
q=1ℏ√2m(0−E).
Como se vê na Fig. 2.1, para fitar toda série de energia de confinamento, a varredura deve conter os valores: −V0<E<0. Ao invés da inspeção ser realizada com números negativos, é preferível utilizar valores positivos. Para isso, pode-se parametrizar a energia:
E=(η−1)V0,
e fazer o parâmetro de energia percorrer os valores: 0<η<1.
5.1 Exemplo numérico
Vamos colocar números nas fórmulas!
Este exemplo considera um DQW de profundidade V0= 0,1 eV
e estrutura 100-20-100 Å, quer dizer, de w= 100 Å e b= 20 Å.
As curvas das Eqs. (5.1) e (5.3),
que foram designadas curva par e curva ímpar, respectivamente,
são apresentadas na Fig. 5.1.
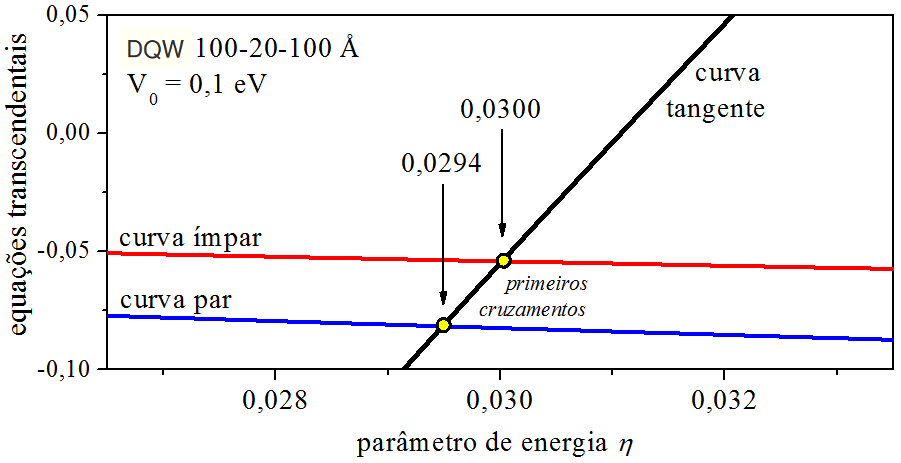
Figura 5.1: Cruzamantos de equações transcendentais.
Os cruzamantos das equações transcendentais revelam os seguintes parâmetros de energia (adimensionais):
η1=0,0294 ← curva par,η2=0,0300 ← curva ˊımpar.
Os parâmetros (5.8) correspondem às seguintes energias de confinamento (meV):
E1=−97,06;E2=−97,00.
O nível de energia é definido como:
ϵ=E+V0.
Já que V0=100 meV, as energias (5.9) correspondem aos seguintes níveis de energia (meV):
ϵ1=2,94;ϵ2=3,00.
Os resultados indicam que o nível de energia do estado fundamental se origina da solução par e que o nível de energia do primeiro estado excitado vem da solução ímpar. A diferença de energia entre os níveis de energia (5.11) é (meV):
ϵ2−ϵ1=0,06.
6 O efeito da espessura da barreira
A energia de confinamento é sensível em relação à espessura da barreira-central, ao valor de b. A função de onda do lado esquerdo do DQW se conecta com a do lado direito, através da barreira-central, mas, se os poços estiverem muito afastados um do outro, a função de onda perde a conexão. Nesse caso, o efeito de tunelamento passa a ser desprezível, e o DQW se comporta como 2-poços simples, individuais. Por exemplo, para o DQW da seção [5.1], o efeito de espessura de barreira sobre os níveis de energia é apresentado na Fig. 6.1.
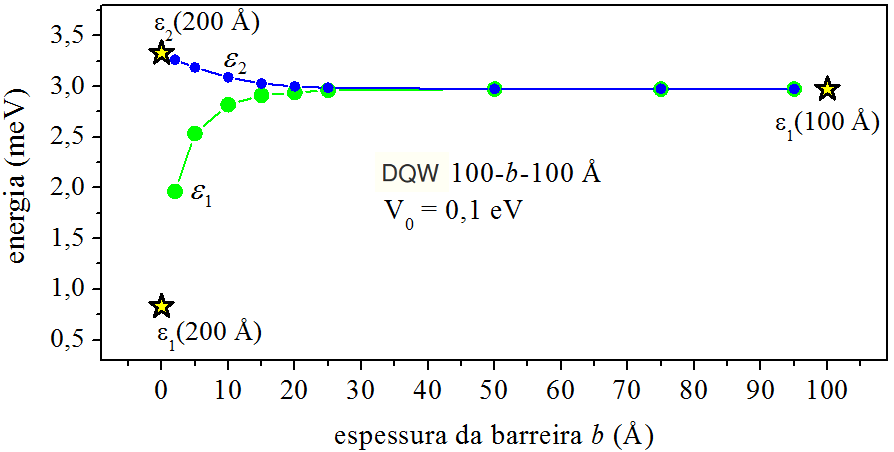
Figura 6.1: Efeito de espessura de barreira. A geometria e profundidade do DQW estão na própria figura.
O aumento da espessura da barreira faz os níveis do DQW (ϵ1,ϵ2) se aproximarem do patamar ϵ1 (100 Å): nível de energia do estado fundamental de um poço simples de largura 100 Å. O efeito do desacoplamento dos poços é nítido, por exemplo, quando a barreira atinge 50 Å de espessura. Nesse caso, o poço duplo (100-50-100 Å) se comporta como um poço simples (100 Å) afastado (e desacoplado) de outro poço simples (100 Å).
Por outro lado, barreiras delgadas (finas) intensificam a diferença entre os níveis do DQW, como se vê, no início da Fig. 6.1. No limite da barreira desaparecer (b→0), o DQW se comporta como um poço simples de largura 2w: O nível de energia ϵ1 tende ao nível de energia do estado fundamental de um poço simples de largura 200 Å, e o nível de energia ϵ2, avizinha-se do nível de energia do primeiro estado excitado desse mesmo poço simples.
O efeito de espessura de barreira é ilustrado na Fig. 6.2
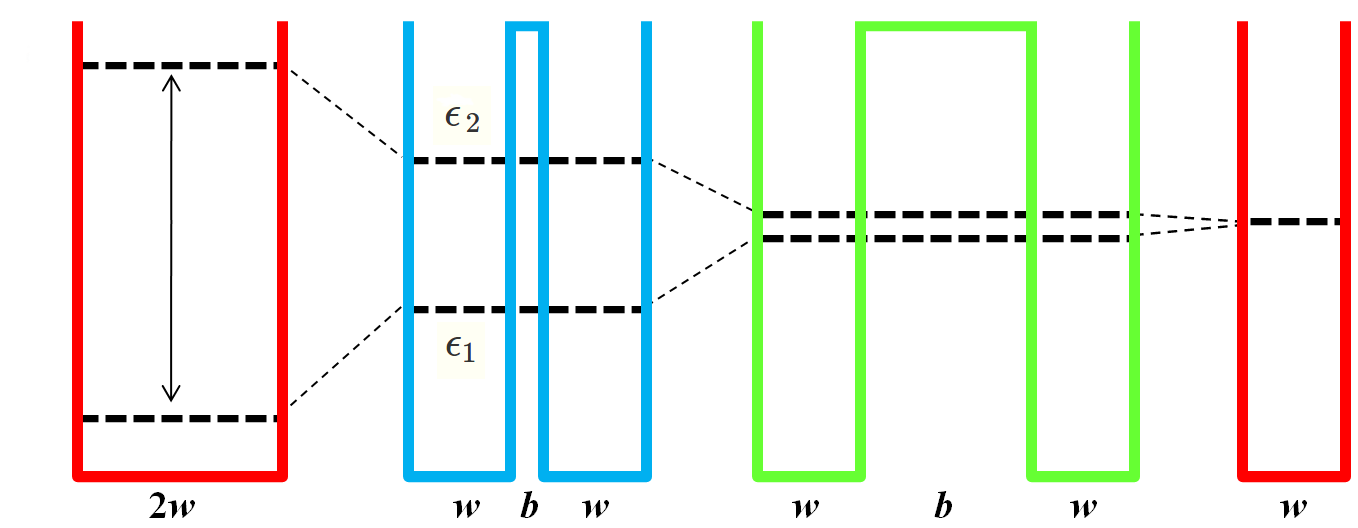
Figura 6.2: Ilustração do efeito de espessura de barreira.
A Fig. 6.3 mostra que a diferença de energia entre os níveis de energia (ϵ2−ϵ1) do DQW da seção [5.1] cai exponencialmente em função da largura da barreira.
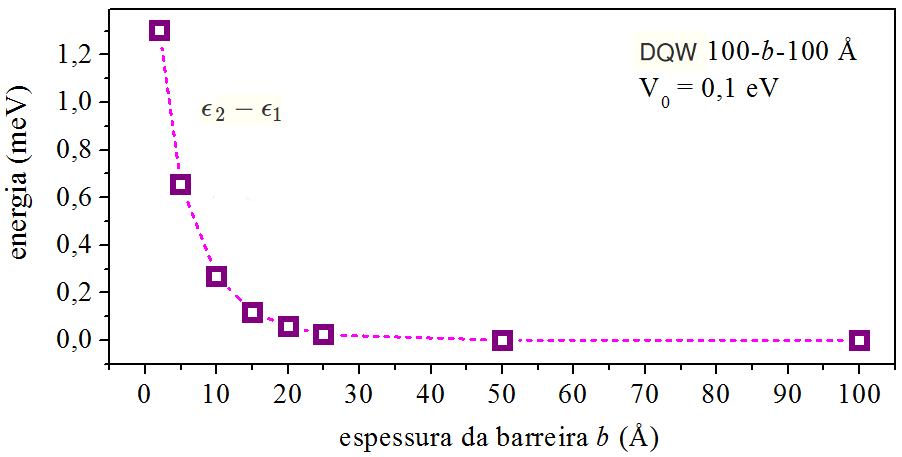
Figura 6.3: Comportamento da diferença de energia entre níveis de energia. A geometria e profundidade do DQW estão na própria figura.
7 A função de onda par
Distribuído pelas seções, há peças para a construção da função de onda de caráter par, que se estende de −∞<x<∞. Cabe, agora, organizar essas peças.
Antes de tudo, precisamos revestir a notação com o fato da energia ser quantizada. Faremos isso, adicionando n à notação:
kn=1ℏ√2m(En+V0),qn=1ℏ√2m(0−En),
Nesta seção, o rótulo n corre entre os números ímpares: n=1,3,5,…
O procedimento é bem simples: Para encontrar a função de onda do lado direto do DQW, divide-se as Eqs. (4.1), (4.2) e (4.10) pela quantidade Q:
P2(x)/Q=(P/Q)cos[knx]+sin[knx],B2(x)/Q=(D/Q)exp[−qnx],Bc(x)/Q=(B/Q)cosh[qnx],
sendo as relações de apoio:
P/Q=(kn/qn)cosh[qn(b/2)]cos[kn(b/2)]−sinh[qn(b/2)]sin[kn(b/2)](kn/qn)cosh[qn(b/2)]sin[kn(b/2)]+sinh[qn(b/2)]cos[kn(b/2)],D/Q={(P/Q)cos[kn(b/2+w)]+sin[kn(b/2+w)]}exp[qn(b/2+w)],B/Q=(P/Q)cos[kn(b/2)]+sin[kn(b/2)]cosh[qn(b/2)].
Agora, o lado esquerdo é o lado negativo (x<0). Vamos chamar os negativos de x− (e os positivos de x+). Então, para encontrar a função de onda do lado esquerdo do DQW, explora-se o fato deste caso de trabalho ser o caso par e, conforme (3.6), a função do lado esquerdo é igual à função do lado direito, logo:
P1(x−)/Q=P2(x+)/Q,B1(x−)/Q=B2(x+)/Q,Bc(x−)/Q=Bc(x+)/Q.
Por exemplo:
B1(−121)/Q=(D/Q)exp[−qn⋅121].
As peças (7.2) e (7.4) constroem a função de onda par em toda extenção do DQW. Mantendo a geometria e profundidade do DQW da seção [5.1], a Fig. 7.1 apresenta a função de onda do estado fundamental — nível de energia ϵ1= 2,94 meV.
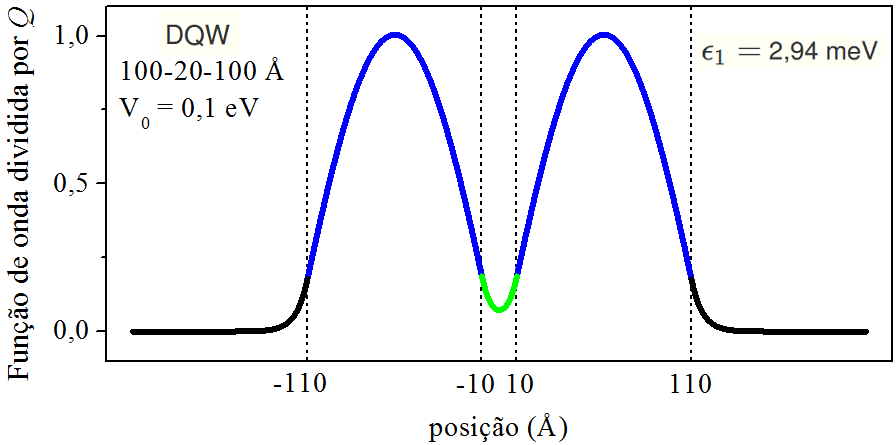
Figura 7.1: Função de onda do estado fundamental. A geometria e profundidade do DQW estão na própria figura.
8 A função de onda ímpar
Deve-se lembrar que a notação do caso ímpar é marcada com uma barra. Também, que as posições do lado esquerdo e direiro são representadas por x− e x+, respectivamente.
Atenção na hora de utilizar os números de onda (7.1): Nesta seção, o rótulo n corre entre os números pares: n=2,4,6,…
Do lado direto do DQW:
ˉP2(x)/ˉQ=(ˉP/ˉQ)cos[knx]+sin[knx],ˉB2(x)/ˉQ=(ˉD/ˉQ)exp[−qnx],ˉBc(x)/ˉQ=(ˉB/ˉQ)sinh[qnx].
Agora, as relações de apoio são:
ˉP/ˉQ=(kn/qn)sinh[qn(b/2)]cos[kn(b/2)]−cosh[qn(b/2)]sin[kn(b/2)](kn/qn)sinh[qn(b/2)]sin[kn(b/2)]+cosh[qn(b/2)]cos[kn(b/2)],ˉD/ˉQ={(ˉP/ˉQ)cos[kn(b/2+w)]+sin[kn(b/2+w)]}exp[qn(b/2+w)],ˉB/ˉQ=(ˉP/ˉQ)cos[kn(b/2)]+sin[kn(b/2)]sinh[qn(b/2)].
E para encerrar, este caso de trabalho é o caso ímpar, segundo (3.7), a função do lado esquerdo é menos igual à função do lado direito:
ˉP1(x−)/ˉQ=−ˉP2(x+)/ˉQ,ˉB1(x−)/ˉQ=−ˉB2(x+)/ˉQ,ˉBc(x−)/ˉQ=−ˉBc(x+)/ˉQ.
Por exemplo:
ˉB1(−121)/ˉQ=−(ˉD/ˉQ)exp[−qn⋅121].
As peças (8.1) e (8.3) montam a função de onda ímpar em toda extenção do DQW. Mantendo a geometria e profundidade do DQW da seção [5.1], a Fig. 8.1 apresenta a função de onda do primeiro estado excitado — nível de energia ϵ2= 3,00 meV.
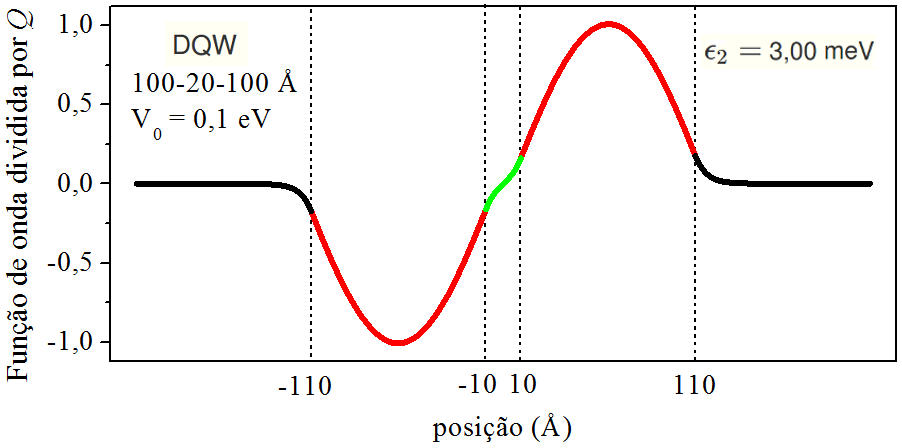
Figura 8.1: Função de onda do primeiro estado excitado. Ver geometria e profundidade do DQW na própria figura.
9 A função de onda normalizada
As seções [7] e [8] deixaram em aberto a quantidade Q. Pode-se dizer que as funções de onda apresentadas nas Figs. 7.1 e 8.1 não estão normalizadas.
O valor de Q é encontrado pelo processo de normalização de função de onda:
∫+∞−∞|Ψ(x)Q|2dx=1|Q|2.
Lembrando que Ψ(x)/Q representa uma função de onda não normalizada,
a Eq. (9.1) nos leva a concluir
que a área debaixo da curva da densidade de probabilidade não-normalizada
é igual à quantidade 1/|Q|2.
O valor de Q está vinculado ao valor de uma área. Há vários softwares que podem calcular áreas de curvas. O método, aqui sugerido, faz uso desses softwares.
Desse modo, tomando as funções de onda das Figs. 7.1 e 8.1, as áreas de suas densidades de probabilidade possuem os valores impressos na Tabela 9.1.
| Função de onda | Área da densidade de probabilidade (m) | Valor de |Q|2 (m−1) |
|---|---|---|
| Par | 1,142×10−8 | 8,757×107 |
| Ímpar | 1,137×10−8 | 8,797×107 |
Os valores da Tabela 9.1 são bem parecidos, isso porque as curvas das densidades de probabilidade são quase idênticas — ver a Fig. 9.1.
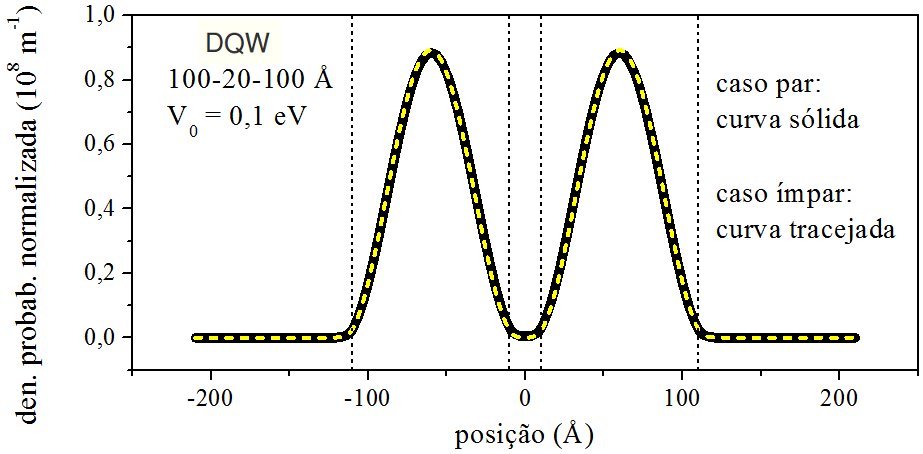
Figura 9.1: Densidade de probabilidade do estado fundamental e do primeiro estado excitado. As curvas estão normalizadas. DQW: Geometria e profundidade na própria figura.
10 Considerações finais
A primeira equação escrita no artigo, Eq. (3.1), estabeleceu o “público-alvo” que se queira atingir. Pode-se dizer que o “publico-alvo” é o elétron no vácuo. Isso é claro, já que a grandeza m, da Eq. (3.1), representa massa de repouso do elétron: m=9,11×10−31 kg. E onde está esse elétron? Não há matéria ao seu redor. O potencial 2.1 que confina o elétron é construído no vácuo.
Então está faltando algo nesse artigo: a matéria!
Poços quânticos não são construídos no vácuo. A indústria de semicondutores investe pesado no desenvolvimento de materiais semicondutores. Faça uma pesquisa sobre o tema. O resultado vai mostrar que são feitos montantes enormes de investimentos para se alcançar uma posição de destaque na indústria de componentes eletrônicos.
O elétron dentro de um material semicondutor se comporta como uma partícula de massa reduzida.
Por exemplo, a massa efetiva do elétron no GaAs é 0,067×9,11×10−31 kg,
ou seja, um valor 15 vezes menor que a massa do elétron no vácuo.
E como o fator
massa reduzidaafeta o valor da energia de confinamento?
Este será o tema do próximo artigo, tendo como título:
Poço Quântico Duplo de Semicondutores.