Função antissimétrica

2-massas, 2-poços; 2-massas, 1-poço; 2-elétrons, 2-poços; 2-elétrons, 1-poço

Saiba qual sistema é formado por partículas distinguíveis e qual é formado por partículas idênticas

Feb 20, 2020 Mais

1 ) Introdução
2 ) A linguagem e notação
3 ) 2-massas, 2-poços
4 ) 2-massas, 1-poço
5 ) 2-elétrons, 2-poços
6 ) 2-elétrons, 1-poço
- 6.1 ) Ao anexar o spin…
Referências

1 ) Introdução

O poço quântico infinito é uma criação imaginária que apresenta solução analítica. Por isso é um objeto didático valioso. O livro (Robinett 2006) dedica três capítulos sobre o tema. Pode-se explicar conceitos de mecânica quântica usando o poço infinito como exemplo.

Este artigo analisa quatro situações de duas partículas confinadas em poços infinitos (ver o título). Em cada caso, conceitos que fundamentam a mecânica quântica são abordados, sendo os principais: partícula não-interativa, estado degenerado, partícula idêntica (férmion e bóson).

Durante a construção das ideias, o estudo desconsidera o spin e focaliza no comportamento espacial da função de onda de 2-partículas (construção e visualização). Apenas na última parte, mostra-se a importância de se anexar o spin ao problema de 2-elétrons.

2 ) A linguagem e notação

Trabalhar com 2-partículas e 2-poços exige linguagem e notação detalhada para se entender equações e interpretar resultados.

Sobre a extensão dos poços:

$\hspace{1cm}$ $a,b \gets$ extremidades de poço;

$\hspace{1cm}$ $\ell = b-a \gets$ largura de poço;

$\hspace{1cm}$ $a_1,b_1 \gets$ extremidades do poço $(1)$;

$\hspace{1cm}$ $\ell _1 = b_1-a_1 \gets$ largura do poço $(1)$;

$\hspace{1cm}$ $a_2,b_2 \gets$ extremidades do poço $(2)$;

$\hspace{1cm}$ $\ell _2 = b_2-a_2 \gets$ largura do poço $(2)$.

Sobre as funções de estado:

$\hspace{1cm}$ $\varphi ^{(1)} \gets$ partícula $(1)$ em estado de poço;

$\hspace{1cm}$ $\varphi ^{(1:\ell_1)} \gets$ partícula $(1)$ em estado do poço $(1)$;

$\hspace{1cm}$ $\varphi ^{(1:\ell_1)} _{n} \gets$ partícula $(1)$ no estado $(n)$ do poço $(1)$;

$\hspace{1cm}$ $\varphi ^{(1:\ell_1)} _{\eta} \gets$ partícula $(1)$ no estado $(\eta)$ do poço $(1)$;

$\hspace{1cm}$ $\varphi ^{(2:\ell_2)} _{n} \gets$ partícula $(2)$ no estado $(n)$ do poço $(2)$;

$\hspace{1cm}$ $\varphi ^{(2:\ell_2)} _{\eta} \gets$ partícula $(2)$ no estado $(\eta)$ do poço $(2)$.

Sobre as posições:

$\hspace{1cm}$ $X \gets$ posição de partícula dentro de poço;

$\hspace{1cm}$ $X ^{(1)} \gets$ posição da partícula $(1)$ dentro de poço;

$\hspace{1cm}$ $X ^{(2)} \gets$ posição da partícula $(2)$ dentro de poço;

$\hspace{1cm}$ $x \gets$ posição geral de partícula pelo eixo $x$;

$\hspace{1cm}$ $x^{(1)} \gets$ posição geral da partícula $(1)$ pelo eixo $x$;

$\hspace{1cm}$ $x^{(2)} \gets$ posição geral da partícula $(2)$ pelo eixo $x$.

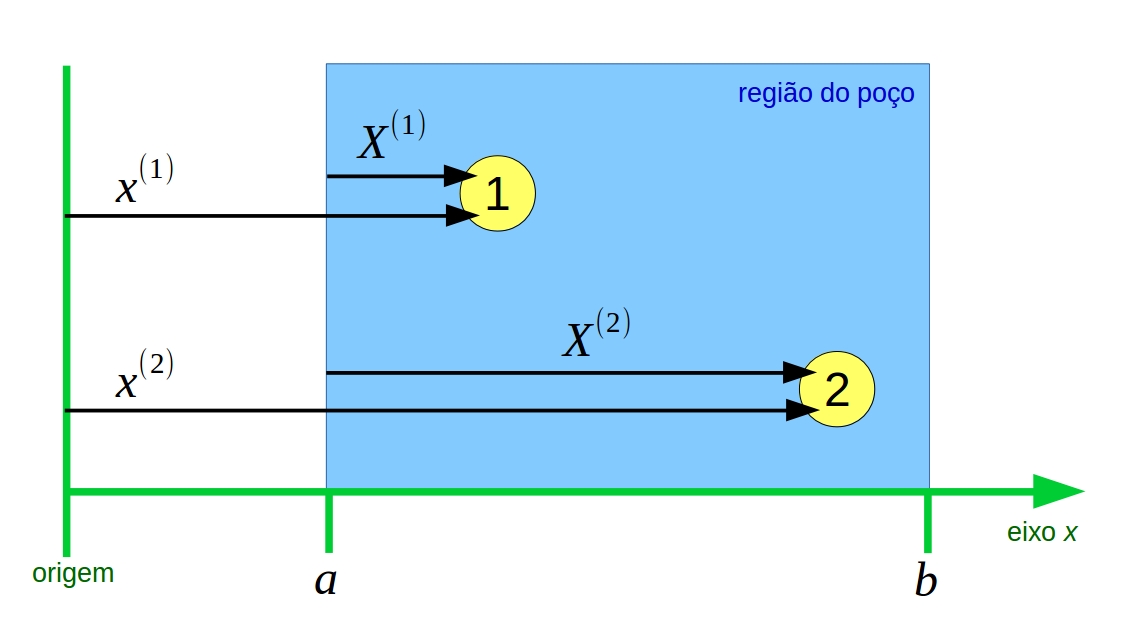
Figura 2.1: Posições da partícula $(1)$ e da partícula $(2)$.

A Figura 2.1 estabelece a relação entre a posição geral e a posição dentro do poço:

\[\begin{equation} x = a + X . \label{eq:P1} \end{equation}\]

A variável $x$, parte da origem, corta a região do poço, e avança interminavelmente. De acordo com a equação $\eqref{eq:P1}$, quando $x=a$, tem-se $X=0$, e tem-se $X=b-a$, quando $x=b$. Então, compreende-se que o intervalo de atuação da variável $X$ é:

\[\begin{equation} 0 \leqslant X \leqslant \ell , \label{eq:P2} \end{equation}\]

ou seja, a variável $X$ tem origem na extremidade esquerda do poço. Por exemplo, para um poço de largura $\ell=100$ (unidades), $X$ vai percorrer de $0$ até $100$, e $X=50$ vai significar um partícula no meio do poço.

Substituindo $\eqref{eq:P1}$ em $\eqref{eq:P2}$, chega-se ao óbvio: Dentro do poço, a variável $x$ assume os valores:

\[\begin{equation} a \leqslant x \leqslant b . \label{eq:P3} \end{equation}\]

Sobre as soluções do poço infinito:

Livros básicos de Mecânica Quântica trazem a solução do poço quântico infinito. Aqui vamos reproduzir o resultado de (Zettili 2009) adaptado à nossa linguagem e notação.

A função de onda de energia no espaço de posição somente é definida dentro do poço, fora, seu valor é zero:

\[\begin{equation} \varphi^{(i:\ell _ j)} _ {n} = \sqrt{\frac{2}{\ell _ j}} \sin \left( \frac{n\pi}{\ell _ j} X^{(i)} \right) , \hspace{1cm} 0 \leqslant X^{(i)} \leqslant \ell _ j . \label{eq:P4} \end{equation}\]

Segundo a definição $\eqref{eq:P1}$,

\[\begin{equation} X^{(i)} = x^{(i)} - a _ j , \label{eq:P5} \end{equation}\]

então, pode-se reescrever $\eqref{eq:P4}$ como:

\[\begin{equation} \begin{aligned} \varphi^{(i:\ell _ j)} _ {n} &= \sqrt{\frac{2}{\ell _ j}} \sin \left( \frac{n\pi}{\ell _ j} \left( x^{(i)} - a _ j \right) \right) , \hspace{1cm} a _ j \leqslant x^{(i)} \leqslant b _ j ,\\ &= 0 , \hspace{6cm} x^{(i)} < a _ j \ \ {\rm e} \ \ x^{(i)} > b _ j . \end{aligned} \label{eq:P6} \end{equation}\]

Nas equações $\eqref{eq:P4}$ – $\eqref{eq:P6}$, o rótulo de partícula é $i=1,2$; e o rótulo de poço é $j=1,2$.

3 ) 2-massas, 2-poços

O primeiro sistema que vamos estudar é ilustrado na Figura 3.1: A partícula $(1)$ se encontra no poço $(1)$, e a partícula $(2)$, no poço $(2)$. A massa da partícula $(1)$ é $m_1$, e da partícula $(2)$, $m_2$. As massas são diferentes: $m_2>m_1$.

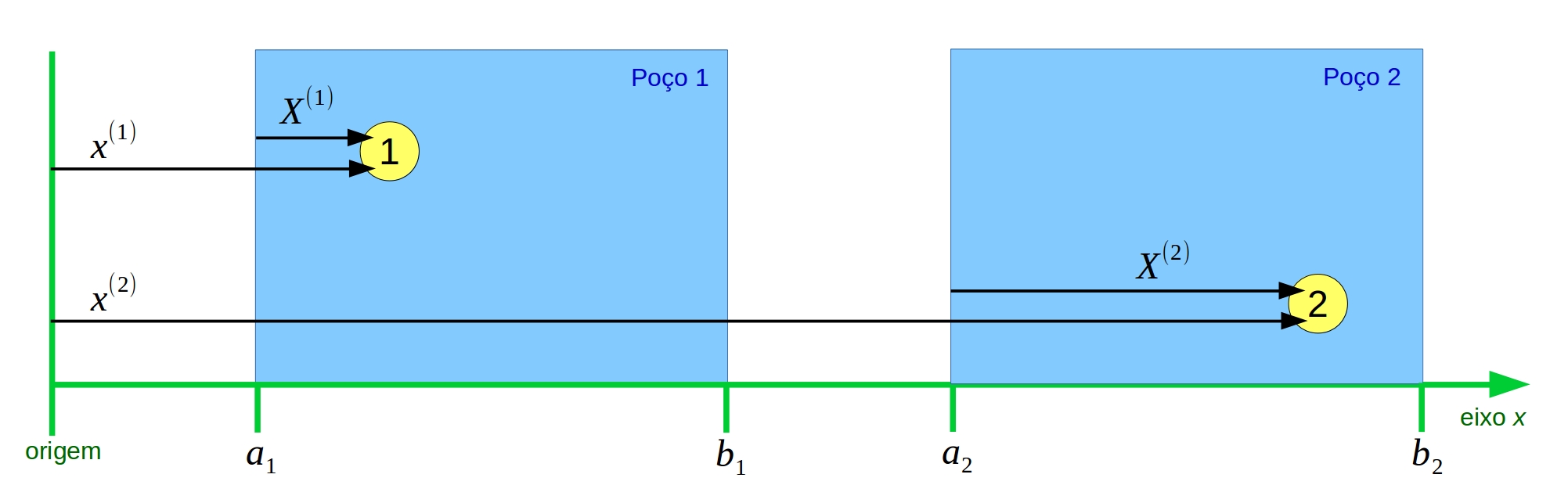
Figura 3.1: Partícula $(1)$, no poço $(1)$, e partícula $(2)$, no poço $(2)$.

A função de estado da partícula $(1)$ é:

\[\begin{equation} \begin{aligned} \varphi^{(1:\ell _ 1)} _ {n} &= \sqrt{\frac{2}{\ell _ 1}} \sin \left( \frac{n\pi}{\ell _ 1} \left( x^{(1)} - a _ 1 \right) \right) , \hspace{1cm} a _ 1 \leqslant x^{(1)} \leqslant b _ 1 ,\\ &= 0 , \hspace{6cm} x^{(1)} < a _ 1 \ \ {\rm e} \ \ x^{(1)} > b _ 1 , \end{aligned} \label{eq:P7} \end{equation}\]

e da partícula $(2)$:

\[\begin{equation} \begin{aligned} \varphi^{(2:\ell _ 2)} _ {\eta} &= \sqrt{\frac{2}{\ell _ 2}} \sin \left( \frac{\eta\pi}{\ell _ 2} \left( x^{(2)} - a _ 2 \right) \right) , \hspace{1cm} a _ 2 \leqslant x^{(2)} \leqslant b _ 2 ,\\ &= 0 , \hspace{6cm} x^{(2)} < a _ 2 \ \ {\rm e} \ \ x^{(2)} > b _ 2 . \end{aligned} \label{eq:P8} \end{equation}\]

A função de estado do sistema de 2-partículas é obtida pelo produto das funções de 1-partícula, quer dizer, fazendo a multiplicação das equações $\eqref{eq:P7}$ e $\eqref{eq:P8}$:

\[\begin{equation} \Psi ^{ (1:\ell _ 1) (2:\ell _ 2) } _ {n, \eta} = \varphi^{(1:\ell _ 1)} _ {n} \varphi^{(2:\ell _ 2)} _ {\eta} . \label{eq:P9} \end{equation}\]

Explicitamente:

\[\begin{equation} \Psi ^{ (1:\ell _ 1) (2:\ell _ 2) } _ {n, \eta} = \frac{2}{\sqrt{\ell _ 1 \ell _ 2}} \sin \left( \frac{n\pi} {\ell _ 1} \left( x^{(1)} - a _ 1 \right) \right) \sin \left( \frac{\eta\pi}{\ell _ 2} \left( x^{(2)} - a _ 2 \right) \right) . \label{eq:P10} \end{equation}\]

A probabilidade (por unidade de área) da partícula $(1)$ estar na posição $x^{(1)}$ e da partícula $(2)$ estar na posição $x^{(2)}$ é:

\[\begin{equation} \left| \Psi ^{ (1:\ell _ 1) (2:\ell _ 2) } _ {n, \eta} \right|^2 = \frac{4}{\ell _ 1 \ell _ 2} \sin^2 \left( \frac{n\pi}{\ell _ 1} \left( x^{(1)} - a _ 1 \right) \right) \sin^2 \left( \frac{\eta\pi}{\ell _ 2} \left( x^{(2)} - a _ 2 \right) \right) . \label{eq:P11} \end{equation}\]

A densidade de probabilidade $\eqref{eq:P11}$, no caso da partícula $(1)$ estar no estado fundamental $(n=1)$ e também a partícula $(2)$ estar no estado fundamental $(\eta=1)$, é:

\[\begin{equation} \left| \Psi ^{ (1:\ell _ 1) (2:\ell _ 2) } _ {1,1} \right|^2 = \frac{4}{\ell _ 1 \ell _ 2} \sin^2 \left( \frac{\pi}{\ell _ 1} \left( x^{(1)} - a _ 1 \right) \right) \sin^2 \left( \frac{\pi}{\ell _ 2} \left( x^{(2)} - a _ 2 \right) \right) . \label{eq:P12} \end{equation}\]

A densidade de probabilidade $\eqref{eq:P12}$ é apresentada na Figura 3.2: Não se usou a constante $\frac{4}{\ell _ 1 \ell _ 2}$, e os valores que dimensionam os poços são arbitrários, $a_1 = 2$, $b_1 = 5$, $a_2 = 6$, $b_2 = 9$, o que implica em $\ell_1=\ell_2=3$.

A inspeção da Figura 3.2 mostra o óbvio: fora das regiões dos poços, a densidade de probabilidade é zero. Por exemplo, $\left|\Psi^{(1:\ell_1)(2:\ell_2)}_{1,1}(3,3)\right|^2=0$, pois, ainda que a partícula $(1)$ possa ocupar a posição $x^{(1)}=3$, a partícula $(2)$ não pode ser encontrada em $x^{(2)}=3$, fora de seu poço de barreiras infinitas. O pico de probabilidade ocorre em $x^{(1)}=3,\!5$ e $x^{(2)}=7,\!5$; o que significa encontar a partícula $(1)$ no centro do poço $(1)$ e a partícula $(2)$ no centro do poço $(2)$.

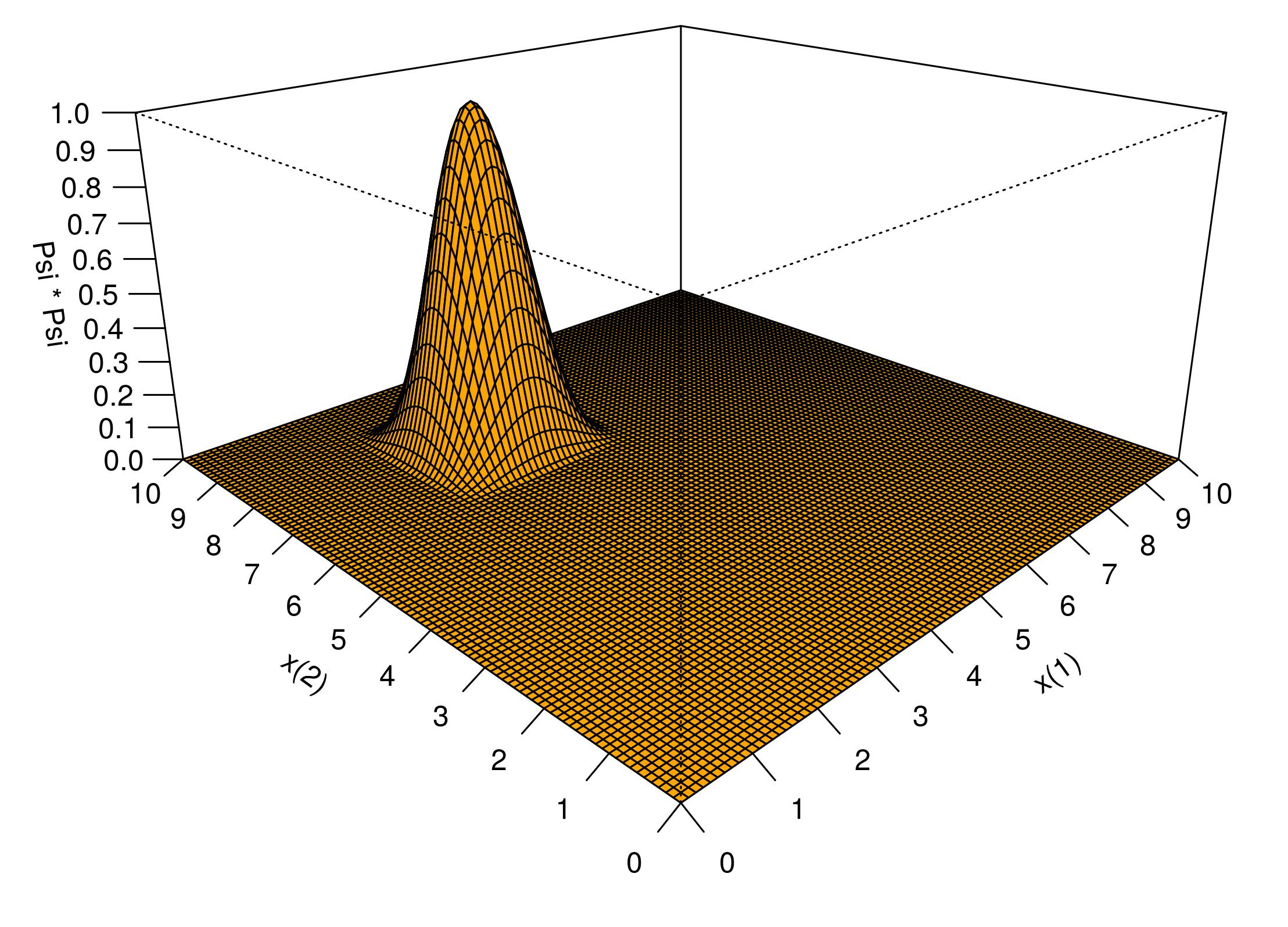
Figura 3.2: 2-Massas, 2-Poços: Densidade de probabilidade do estado fundamental.

O primeiro estado excitado depende das massas, como fizemos $m_2>m_1$, e pelo fato da energia se inversamente proporcional à massa, ele acontece quando a partícula $(1)$ está no estado fundamental $(n=1)$ e a partícula $(2)$ está no primeiro estado excitado $(\eta=2)$:

\[\begin{equation} \left| \Psi ^{ (1:\ell _ 1) (2:\ell _ 2) } _ {1,2} \right|^2 = \frac{4}{\ell _ 1 \ell _ 2} \sin^2 \left( \frac{\pi}{\ell _ 1} \left( x^{(1)} - a _ 1 \right) \right) \sin^2 \left( \frac{2\pi}{\ell _ 2} \left( x^{(2)} - a _ 2 \right) \right) . \label{eq:P13} \end{equation}\]

A densidade de probabilidade $\eqref{eq:P13}$ é apresentada na Figura 3.3. Ocorrem 2 picos de probabilidade: o primeiro em $x^{(1)}=3,\!5$ e $x^{(2)}=6,\!75$; e o segundo em $x^{(1)}=3,\!5$ e $x^{(2)}=8,\!25$. Como se vê, a partícula $(2)$ não pode ser encontrada no meio de seu poço, pois a densidade de probabilidade é zero em $x^{(2)}=7,\!5$.

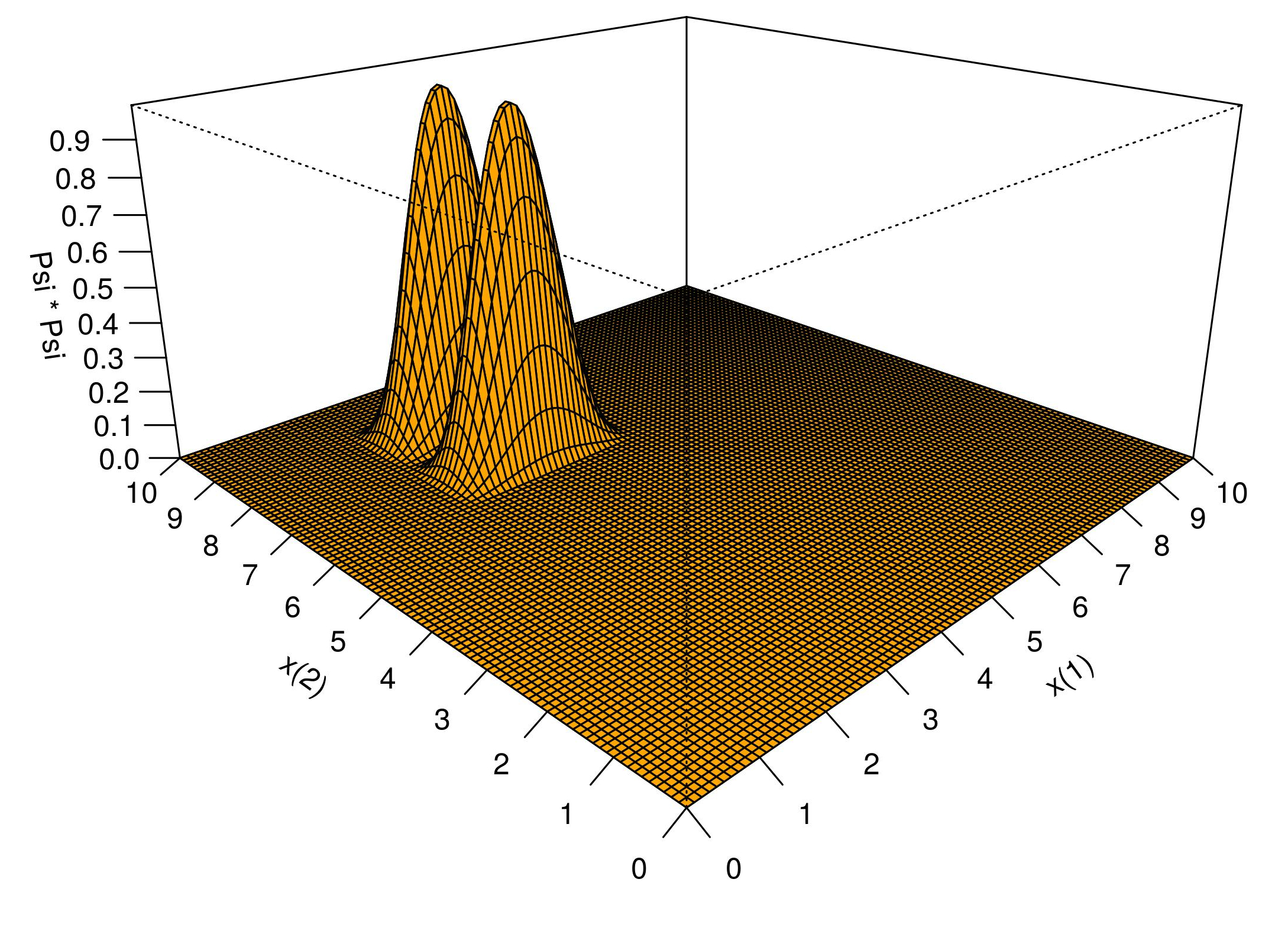
Figura 3.3: 2-Massas, 2-Poços: Densidade de probabilidade do primeiro estado excitado.

4 ) 2-massas, 1-poço

Vamos agora situar as 2-partículas $(m_2>m_1)$ em um mesmo poço. O sistema que vamos estudar é ilustrado na Figura 2.1:

$\hspace{1cm}$ $a_1 = a_2 = a \gets$ extremidade esquerda do poço;

$\hspace{1cm}$ $b_1 = b_2 = b \gets$ extremidade direita do poço;

$\hspace{1cm}$ $\ell_1 = \ell_2 = \ell \gets$ largura do poço.

Vamos também colocar a extremidade esquerda do poço na origem do eixo $x$: $a=0$.

As funções de 1-partícula $\eqref{eq:P7}$ e $\eqref{eq:P8}$, a função de 2-partículas $\eqref{eq:P10}$ e sua densidade de probabilidade $\eqref{eq:P11}$, passam a ser escritas como:

\[\begin{equation} \begin{aligned} \varphi^{(1:\ell)} _ {n} &= \sqrt{\frac{2}{\ell}} \sin \left( \frac{n\pi}{\ell} x^{(1)} \right) , \hspace{1cm} 0 \leqslant x^{(1)} \leqslant \ell ,\\ &= 0 , \hspace{4cm} x^{(1)} < 0 \ \ {\rm e} \ \ x^{(1)} > \ell ,\\ \varphi^{(2:\ell)} _ {\eta} &= \sqrt{\frac{2}{\ell}} \sin \left( \frac{\eta\pi}{\ell} x^{(2)} \right) , \hspace{1cm} 0 \leqslant x^{(2)} \leqslant \ell ,\\ &= 0 , \hspace{4cm} x^{(2)} < 0 \ \ {\rm e} \ \ x^{(2)} > \ell ,\\ \end{aligned} \label{eq:P14} \end{equation}\]

\[\begin{equation} \begin{aligned} \Psi ^{ (1:\ell) (2:\ell) } _ {n, \eta} &= \frac{2}{\ell} \sin \left( \frac{n\pi} {\ell} x^{(1)} \right) \sin \left( \frac{\eta\pi}{\ell} x^{(2)} \right) ,\\ \left| \Psi ^{ (1:\ell) (2:\ell) } _ {n, \eta} \right|^2 &= \frac{4}{\ell^2} \sin^2 \left( \frac{n\pi}{\ell} x^{(1)} \right) \sin^2 \left( \frac{\eta\pi}{\ell} x^{(2)} \right) . \end{aligned} \label{eq:P15} \end{equation}\]

No caso das 2 partículas estarem no estado fundamental $(n=1,\eta=1)$, a densidade de probabilidade $\eqref{eq:P15}$ é apresentada na Figura 4.1: Não se usou a constante $\frac{4}{\ell^2}$, e a largura do poço é arbitrária: $\ell=3$.

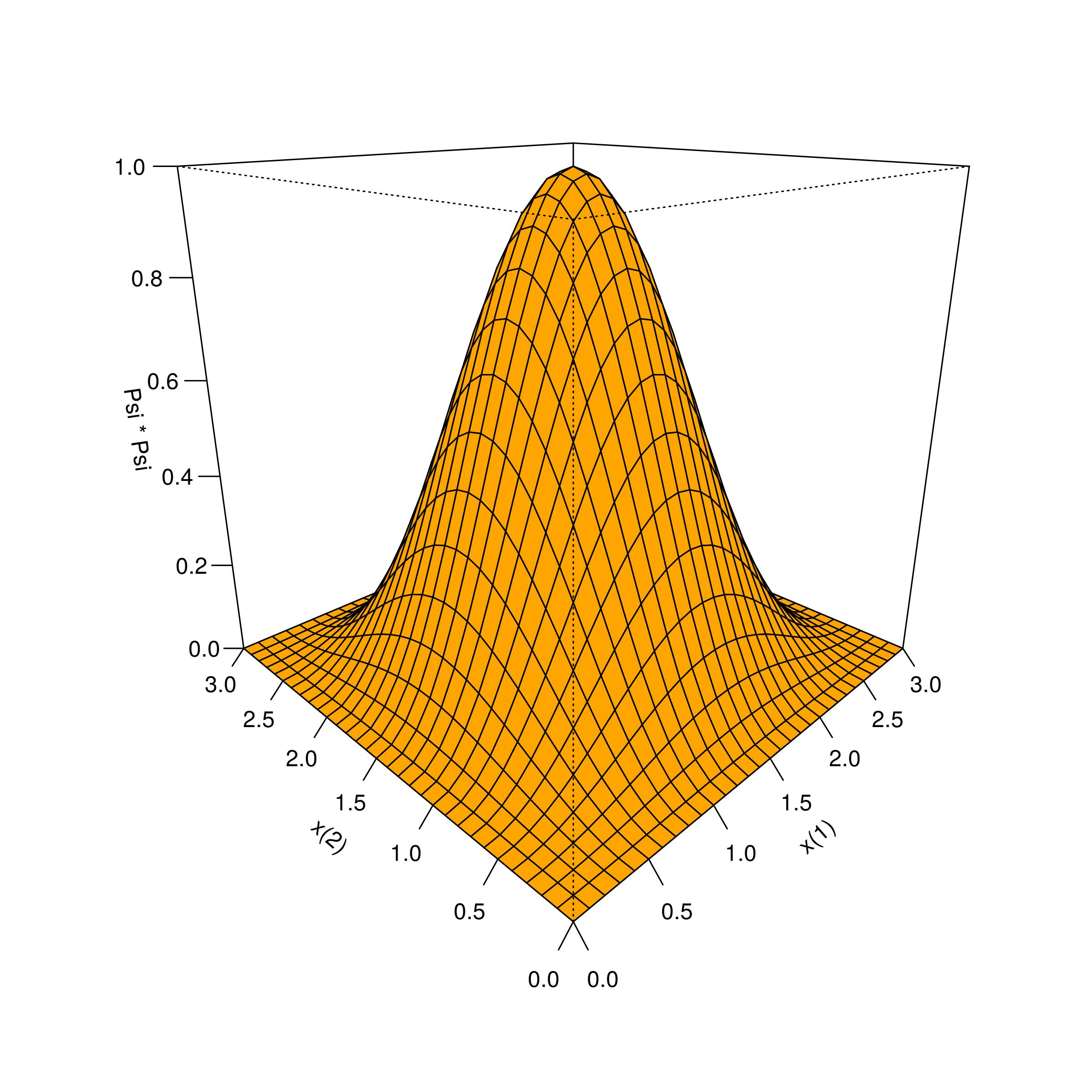
Figura 4.1: 2-Massas, 1-Poço: Densidade de probabilidade do estado fundamental.

Agora, no caso da partícula $(1)$ estar no estado fundamental $(n=1)$ e a partícula $(2)$ no primeiro estado excitado $(\eta=2)$, a densidade de probabilidade $\eqref{eq:P15}$ é apresentada na Figura 4.2.

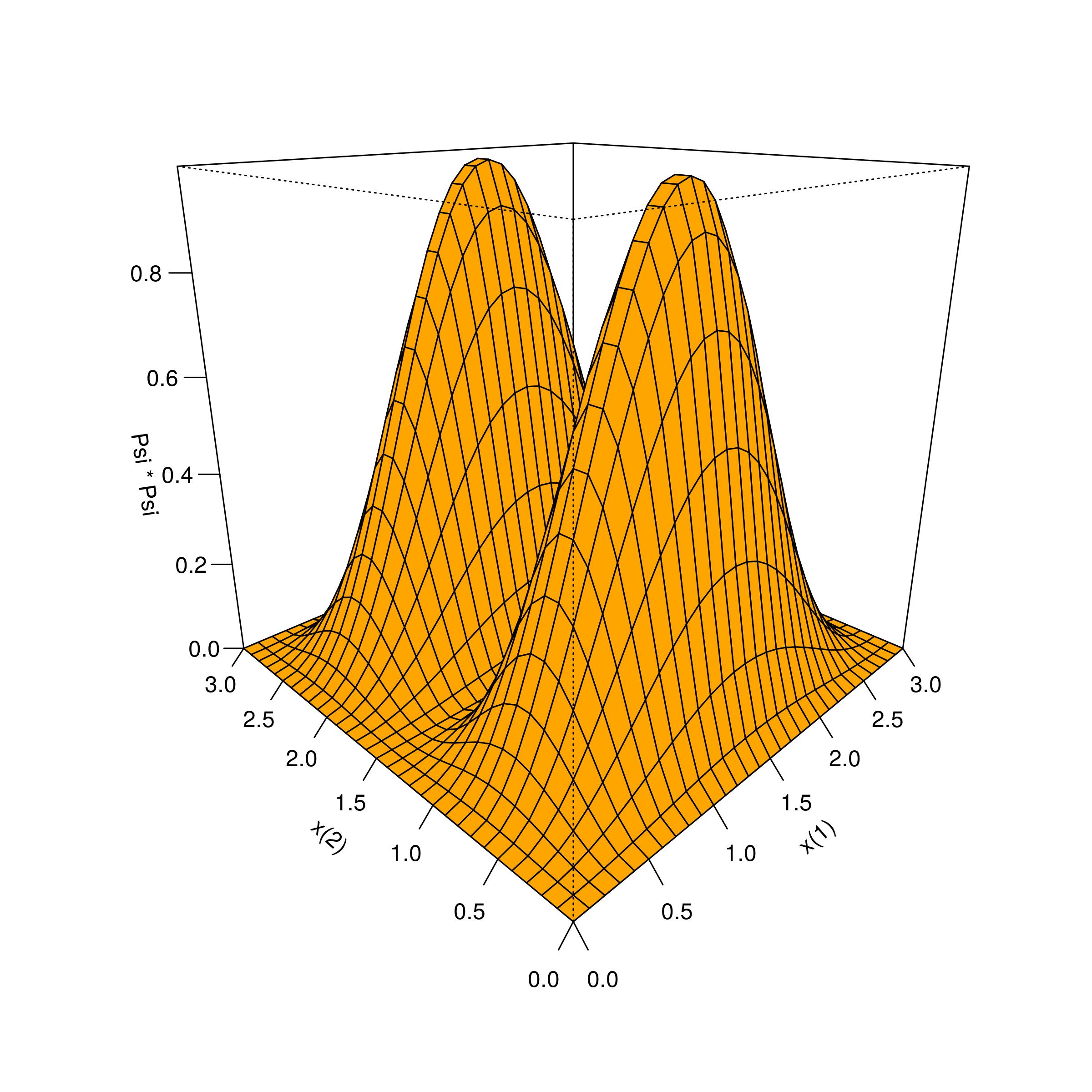
Figura 4.2: 2-Massas, 1-Poço: Densidade de probabilidade do primeiro estado excitado.

A comparação das densidades de probabilidade do sistema (2-Massas, 1-Poço), desta seção, com as densidades de probabilidade do sistema (2-Massas, 2-Poços), da seção anterior, nos induz a pensar que os dois sistemas são iguais — porém, não são!

As partículas no sistema (2-Massas, 2-Poços) estão separadas por natureza. Uma não pode interagir com a outra, afetando ou influenciando o desenvolvimento ou a condição da outra. O sistema (2-Massas, 2-Poços) é um sistema de partículas não-interativas, por natureza. Todavia, no sistema (2-Massas, 1-Poço) as partículas se localizam no mesmo poço. Então, o que impede de “conversarem” ou interagirem?

— A nossa mente!

Do ponto de vista teórico, desprezamos a interação partícula-partícula. Idealizamos um sistema em que cada partícula “vive” isolada em seu próprio poço. Por estratégia teórica, consideramos o sistemas como um sistema de partículas não-interativas. Fazendo isso, a equação de Schrödinger de N-partículas é separada em N-equações de 1-partícula, e a função de estado de N-partículas é expressa como o produto de N-funções de estado de 1-partícula, e a energia do sistema de N-partículas é expressa como a soma de N-energias de 1-partícula:

\[\begin{equation} \begin{aligned} \Psi \left( x^{(1)}, x^{(2)}, \cdots , x^{(N)} \right) &= \varphi \left( x^{(1)} \right) \varphi \left( x^{(2)} \right) \cdots \varphi \left( x^{(N)} \right) ,\\ E &= \varepsilon _ 1 + \varepsilon _ 2 + \cdots + \varepsilon _ N . \end{aligned} \label{eq:P16} \end{equation}\]

Em conclusão, no sistema (2-Massas, 2-Poços), as partículas são isoladas por natureza, entretanto, no sistema (2-Massas, 1-Poço), as partículas estão isoladas por estratégia teórica.

5 ) 2-elétrons, 2-poços

O sistema (2-Elétrons, 2-Poços) é um sistema de partículas isoladas fisicamente (corporalmente), não-interativas por natureza. À primeira vista, pode-se pensar que ele é igual ao sistema (2-Massas, 2-Poços) — porém, não é! No sistema (2-Massas, 2-Poços) as massas são diferentes: $m_2>m_1$. No sistema (2-Elétrons, 2-Poços) as massas são iguais: a massa de repouso do elétron é $m_e=9,1\times10^{-31} {\rm kg}$.

As massas serem iguais não afeta a estrutura do estado fundamental: A Figura 3.2 também pode representar a densidade de probabilidade do estado fundamental do sistema (2-Elétrons, 2-Poços). Mas afeta a estrutura do primeiro estado excitado. O primeiro estado excitado do sistema (2-Elétrons, 2-Poços) é degenerado. Em termos de energia, estar o elétron $(1)$ no estado fundamental $(n=1)$ e o elétron $(2)$ no primeiro estado excitado $(\eta=2)$, ou, estar o elétron $(1)$ no primeiro estado excitado $(n=2)$ e o elétron $(2)$ no estado fundamental $(\eta=1)$, não há diferença, quer dizer, $\Psi^{(1:\ell_1)(2:\ell_2)}_{1,2}$ e $\Psi^{(1:\ell_1)(2:\ell_2)}_{2,1}$ são estados de mesma energia.

A Figura 5.1 mostra a densidade de probabilidade do estado $\Psi^{(1:\ell_1)(2:\ell_2)}_{2,1}$, compare com a densidade de probabilidade do estado $\Psi^{(1:\ell_1)(2:\ell_2)}_{1,2}$ — impressa na Figura 3.3. Como se vê na 5.1, agora é a partícula $(1)$ que não pode ser encontrada no meio de seu poço, pois a densidade de probabilidade é zero em $x^{(1)}=3,\!5$ — na Figura 3.3, é a partícula $(2)$ que não pode ser encontrada no meio de seu poço.

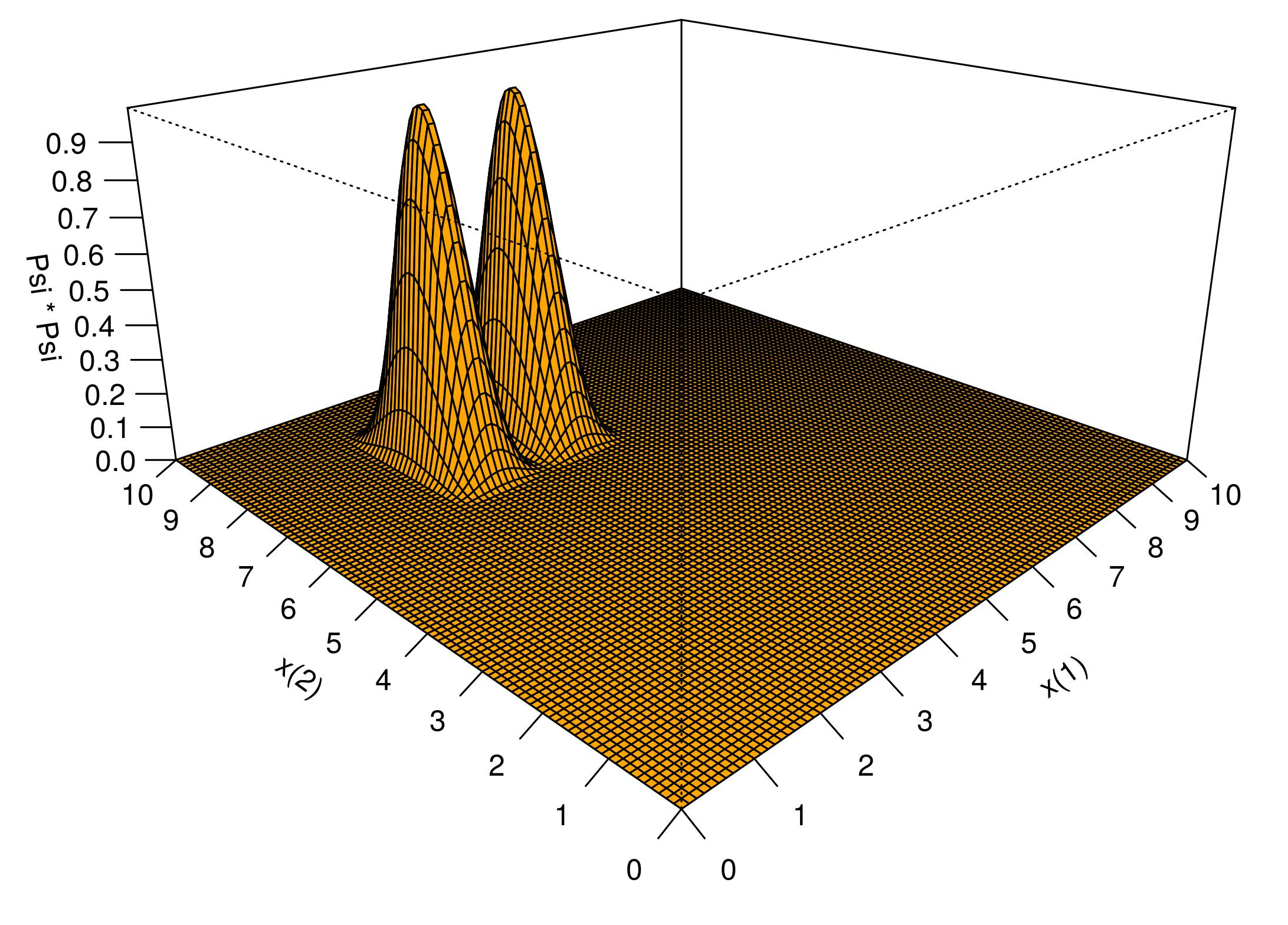
Figura 5.1: 2-Elétrons, 2-Poços: Uma das densidade de probabilidade do primeiro estado excitado.

6 ) 2-elétrons, 1-poço

O sistema (2-Elétrons, 1-Poço) é um sistema de partículas interativas. A interação elétron-elétron é do tipo Coulombiana. No nosso caso, que é um caso unidimensional, a repulsão elétron-elétron se escreve:

\[\begin{equation} V = \frac{e^2}{\left| x^{(1)} - x^{(2)} \right|} . \label{eq:P17} \end{equation}\]

Negligenciando $\eqref{eq:P17}$, pode-se considerar os elétrons como partículas não-interativas (por estratégia teórica, não por natureza).

À primeira vista, pode-se pensar que o sistema (2-Elétrons, 1-Poço) seja direfente do sistema (2-Massas, 1-Poço) apenas na questão das massas, e que a equação $\eqref{eq:P15}$ ainda é válida. Entretanto, há um novo fator:

$\hspace{3cm}$ — Elétrons são partículas idênticas.

Partículas $(i)$ com massas $m_i$ são partículas distinguíveis.

Elétrons $(i)$ com massas $m_i=m_e$ são partículas indistinguíveis (idênticas): Colocados em poços diferentes $(V_i)$ são partículas distinguíveis, mas, colocados em um mesmo poço $(V_i=V_1)$ são partículas idênticas. Por isso, no caso da seção anterior, foram considerados partículas distinguíveis, no caso desta seção, serão tratados como partículas idênticas.

Um sistema de partículas distinguíveis possui função de estado do tipo $\eqref{eq:P16}$, mas, um sistema de partículas idênticas, não.

A função de estado de um sistema de partículas idênticas precisa ser simétrica ou antissimétrica:

$\hspace{1cm}$ Função simétrica $\gets$ Se ocorrer o intercâmbio de um par de partículas, o sinal da função não troca de sinal;

$\hspace{1cm}$ Função antissimétrica $\gets$ Se ocorrer o intercâmbio de um par de partículas, o sinal da função troca de sinal.

Sobre a notação, será empregado “$s$” para indicar a função de estado simétrica e “$a$” para indicar a antissimétrica:

$\hspace{1cm}$ $\Psi ^{s} _ {n,\eta} \gets$ função de estado simétrica;

$\hspace{1cm}$ $\Psi ^{a} _ {n,\eta} \gets$ função de estado antissimétrica.

Partículas idênticas que possuem spin meio-inteiro são denominadas férmions, as que possuem spin inteiro, bósons. Um sistema de férmions é representado por função de estado antissimétrica, um sistema de bósons, por função de estado simétrica:

$\hspace{3cm}$ — Elétrons são partículas idênticas que possuem spin meio-inteiro: são férmions;

$\hspace{3cm}$ — Um sistema de elétrons é representado por função de estado antissimétrica.

A função antissimétrica pode ser construída com o auxílio do determinante de Slater (Zettili 2009). Para um sistema com 2-elétrons, o resultado é:

\[\begin{equation} \Psi ^{a} _ {n,\eta} = \frac{1}{\sqrt{2}} \left( \varphi ^ {(1:\ell)} _ {n} \varphi ^ {(2:\ell)} _ {\eta} - \varphi ^ {(1:\ell)} _ {\eta} \varphi ^ {(2:\ell)} _ {n} \right) . \label{eq:P18} \end{equation}\]

Vendo $\eqref{eq:P18}$ é fácil de descobrir que a função simétrica é do seguinte modo:

\[\begin{equation} \Psi ^{s} _ {n,\eta} = \frac{1}{\sqrt{2}} \left( \varphi ^ {(1:\ell)} _ {n} \varphi ^ {(2:\ell)} _ {\eta} + \varphi ^ {(1:\ell)} _ {\eta} \varphi ^ {(2:\ell)} _ {n} \right) . \label{eq:P19} \end{equation}\]

Descarregando as soluções do poço infinito em $\eqref{eq:P18}$, a função antissimétrica tem a feição:

\[\begin{equation} \Psi ^{a} _ {n,\eta} = \frac{\sqrt{2}}{\ell} \left[ \sin \left( \frac{n\pi} {\ell} x^{(1)} \right) \sin \left( \frac{\eta\pi}{\ell} x^{(2)} \right) -\\ \sin \left( \frac{\eta\pi}{\ell} x^{(1)} \right) \sin \left( \frac{n\pi} {\ell} x^{(2)} \right) \right] . \label{eq:P20} \end{equation}\]

A função $\eqref{eq:P20}$ é uma função espacial. Sobre os valores de $x^{(1)}$ e $x^{(2)}$, deve-se lembrar que os 2-elétrons estão confinados em um poço de extensão $\ell$, então, eles podem ser encontrados dentro do mesmo intervalo: $\left(0 \leqslant x^{(1)} \leqslant \ell \right)$; $\left(0 \leqslant x^{(2)} \leqslant \ell\right)$.

A função $\eqref{eq:P20}$ para o estado fundamental $(n=1,\eta=1)$ é:

\[\begin{equation} \Psi ^{a} _ {1,1} = \frac{\sqrt{2}}{\ell} \left[ \sin \left( \frac{\pi}{\ell} x^{(1)} \right) \sin \left( \frac{\pi}{\ell} x^{(2)} \right) - \sin \left( \frac{\pi}{\ell} x^{(1)} \right) \sin \left( \frac{\pi}{\ell} x^{(2)} \right) \right] . \label{eq:P21} \end{equation}\]

É óbvio que $\eqref{eq:P21}$ não existe: A função espacial antissimétrica para o estado fundamental é nula.

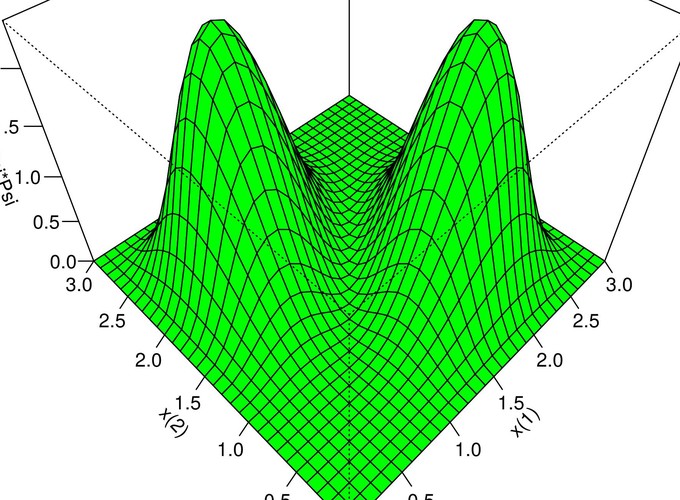
A função $\eqref{eq:P20}$ para o primeiro estado excitado $(n=1,\eta=2)$ não é toda nula:

\[\begin{equation} \Psi ^{a} _ {1,2} = \frac{\sqrt{2}}{\ell} \left[ \sin \left( \frac{\pi}{\ell} x^{(1)} \right) \sin \left( \frac{2\pi}{\ell} x^{(2)} \right) -\\ \sin \left( \frac{2\pi}{\ell} x^{(1)} \right) \sin \left( \frac{\pi}{\ell} x^{(2)} \right) \right] . \label{eq:P22} \end{equation}\]

A função espacial simétrica equivalenta à $\eqref{eq:P22}$ é:

\[\begin{equation} \Psi ^{s} _ {1,2} = \frac{\sqrt{2}}{\ell} \left[ \sin \left( \frac{\pi}{\ell} x^{(1)} \right) \sin \left( \frac{2\pi}{\ell} x^{(2)} \right) +\\ \sin \left( \frac{2\pi}{\ell} x^{(1)} \right) \sin \left( \frac{\pi}{\ell} x^{(2)} \right) \right] . \label{eq:P23} \end{equation}\]

As densidades de probabilidade $\left|\Psi ^{a} _ {1,2}\right|^2$ e $\left|\Psi ^{s} _ {1,2}\right|^2$ são apresentadas nas Figuras 6.1 e 6.2, respectivamente: Não se usou a constante $\frac{2}{\ell^2}$, e a largura do poço é arbitrária: $\ell=3$.

A figura antissímétrica (6.1) apresenta pontos com densidade de probabilidade nula. Por exemplo, o resultado da equação $\eqref{eq:P22}$ para $x^{(1)}=x^{(2)}=2$ e $\ell=3$ é:

\[\begin{equation} \Psi ^{a} _ {1,2} (2,2) = \frac{\sqrt{2}}{\ell} \left[ \sin \left( \frac{2\pi}{3} \right) \sin \left( \frac{4\pi}{3} \right) - \sin \left( \frac{4\pi}{3} \right) \sin \left( \frac{2\pi}{3} \right) \right] = 0 . \label{eq:P24} \end{equation}\]

Generalizando, a reta $x^{(1)}=x^{(2)}$ apresenta densidade de probabilidade nula:

$\hspace{3cm}$ — O elétron $(1)$ não ocupa o mesmo espaço do elétron $(2)$.

A situação muda quando se analisa a figura simétrica (6.2). Agora ocorre um pico de probabilidade em $x^{(1)}=x^{(2)}$:

$\hspace{3cm}$ — O bóson $(1)$ ocupa o mesmo espaço do bóson $(2)$.

Os pontos mais prováveis de se encontar o sistema (2-Elétrons, 1-Poço) são $\left[ x^{(1)}=0,\!9 ; x^{(2)} =2,\!1 \right]$ e $\left[ x^{(1)}=2,\!1 ; x^{(2)} =0,\!9 \right]$, que correspondem aos picos da Figura (6.1). Como se vê, os elétrons preferem ficar em lugares opostos.

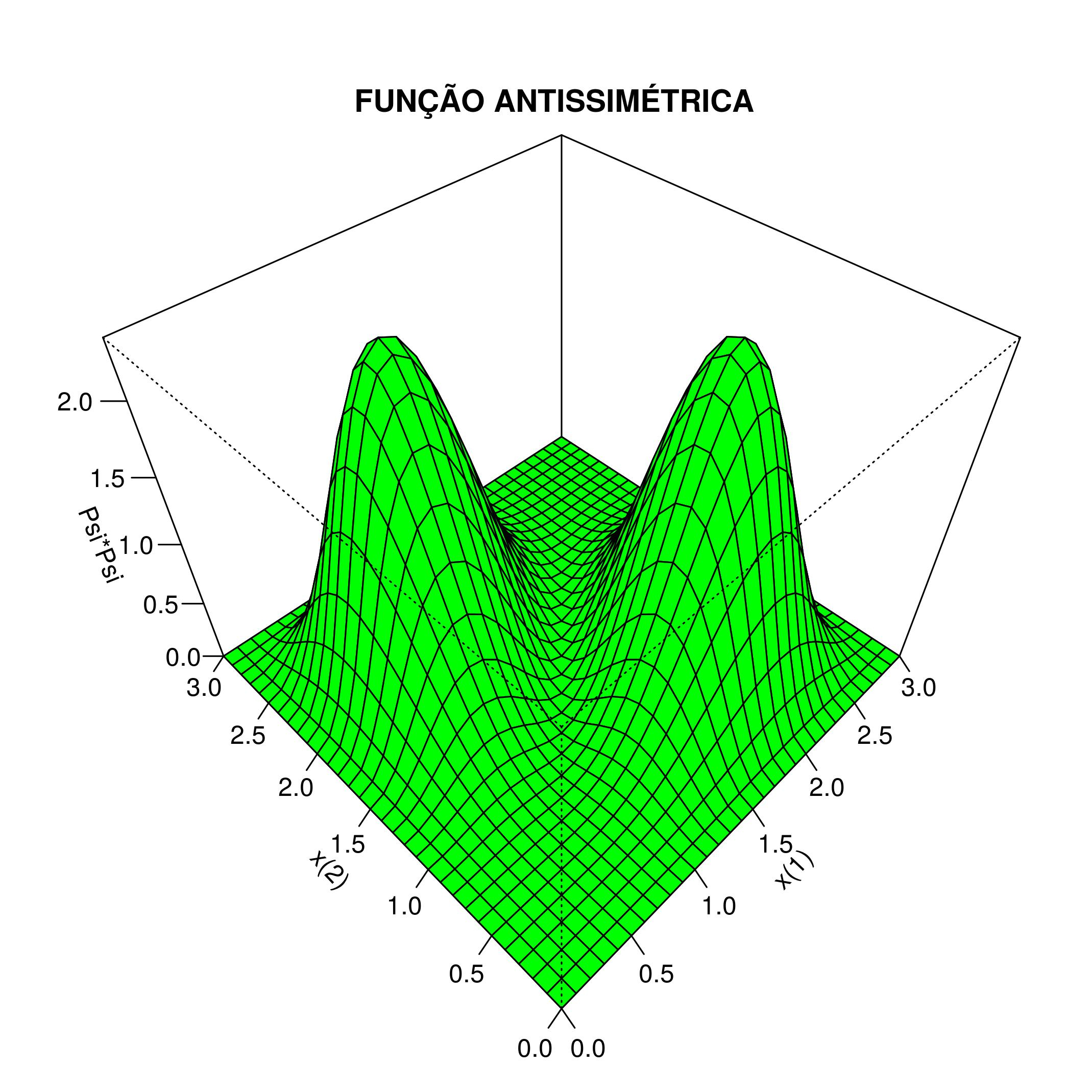
Figura 6.1: 2-Elétrons, 1-Poço: Densidade de probabilidade do primeiro estado excitado.

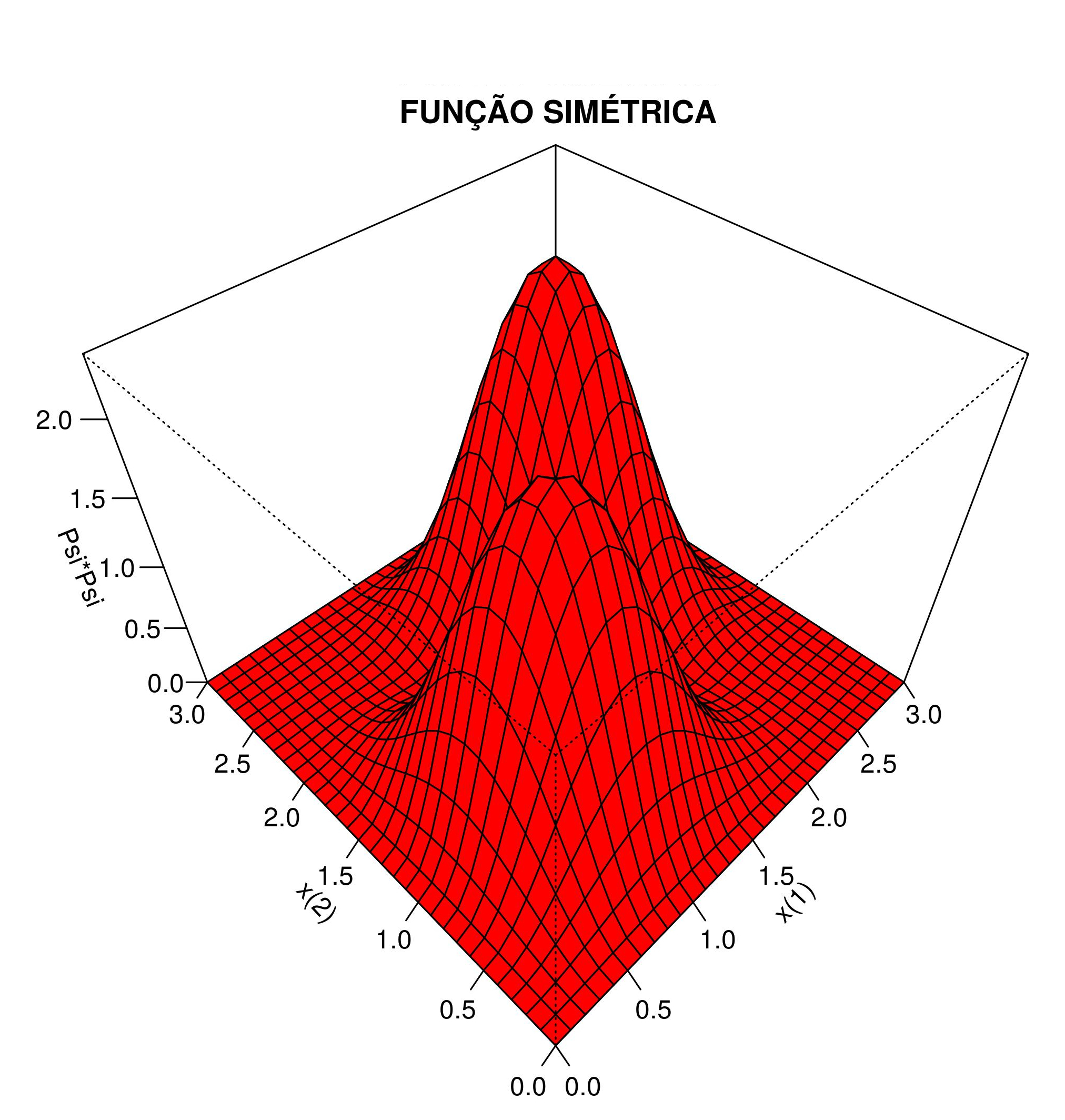
$Densidade de probabilidade de sistema com 2-bósons (equivalente simétrico da Figura \@ref(fig:FIG8)).$

Figura 6.2: Densidade de probabilidade de sistema com 2-bósons (equivalente simétrico da Figura 6.1).

6.1 ) Ao anexar o spin…

O artigo Multipletos de (2,3)-Spins-1/2 trata do acoplamento de (2,3)-spins-1/2. Esse tipo de acoplamento dá origem a um tripleto e a um singleto. A estrutura do tripleto é simétrica, e a do singleto é antissimétrica.

Este artigo mostrou que a função espacial antissimétrica do sistema (2-Elétrons, 1-Poço), estado fundamental, é nula — ver a equação $\eqref{eq:P21}$. Isso não quer dizer que não exista o estado fundamental para o sistema de 2-elétrons. Quer dizer, apenas, que falta acrescentar o spin no problema.

Constrói-se uma função antissimétrica multipicando uma função espacial simétrica com uma função de spin antissimétrica.

Ao tratar o estado fundamental $(n=1, \eta=1)$, a função antissimétrica é construída pela multiplicação da função espacial $\eqref{eq:P19}$ (simétrica) com a função singleto (antissimétrica):

\[\begin{equation} \Psi ^{a} _ {1,1} = \frac{1}{\sqrt{2}} \left( \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {1} + \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {1} \right) {\rm \ * \ } {\rm singleto} . \label{eq:P25} \end{equation}\]

Resolvendo dentro dos parênteses:

\[\begin{equation} \Psi ^{a} _ {1,1} = \frac{2}{\sqrt{2}} {\rm \ * \ } \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {1} {\rm \ * \ } {\rm singleto} . \label{eq:P26} \end{equation}\]

No estado com 2-spins-1/2 acoplados resultando em spin total zero (singleto), o spin do elétron $(1)$ está ao contrário do spin do elétron $(2)$, por exemplo, um está para cima e outro, para baixo.

O coeficiente $\varphi^{(1:\ell)}_{1} \varphi^{(2:\ell)}_{1}$ pode ser interpretado como amplitude de probabilidade do estado singleto, ou seja, $\left| \varphi^{(1:\ell)}_{1} \varphi^{(2:\ell)}_{1} \right|^2$ é a probabilidade (por unidade de área) de achar o sistema no estado singleto.

O perfil da densidade de probabilidade $\left| \varphi^{(1:\ell)}_{1} \varphi^{(2:\ell)}_{1} \right|^2$ é apresentado na Figura 4.1: A reta $x^{(1)}=x^{(2)}$ apresenta densidade de probabilidade não-nula.

Ao anexar o spin, o que parecia impossível (elétrons ocuparem o mesmo espaço), passa a ter probabilidade de ocorrer. Quando os elétrons estão com a mesma energia $(n=1, \eta=1)$, o elétron $(1)$, na posição $x^{(1)}$, se acopla (via spin) com elétron $(2)$, na posição $x^{(2)}=x^{(1)}$, e formam um sistema com spin total zero:

$\hspace{3cm}$ — O elétron $(1)$, com spin contrário ao outro, ocupa o mesmo espaço do outro.

Também constrói-se uma função antissimétrica multipicando uma função espacial antissimétrica com uma função de spin simétrica.

Ao tratar o primeiro estado excitado $(n=1, \eta=2)$, a função antissimétrica é construída pela multiplicação da função espacial $\eqref{eq:P18}$ (antissimétrica) com a função tripleto (simétrica):

\[\begin{equation} \Psi ^{a} _ {1,2} = \frac{1}{\sqrt{2}} {\rm \ * \ } \left( \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {2} - \varphi ^ {(1:\ell)} _ {2} \varphi ^ {(2:\ell)} _ {1} \right) {\rm \ * \ } {\rm tripleto} . \label{eq:P27} \end{equation}\]

No estado com 2-spins-1/2 acoplados resultando em spin total 1 (tripleto), há uma configuração em que os 2-spins estão para cima, e há outra, em que os 2-spins estão para baixo.

Interpreta-se que $\left| \left( \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {2} - \varphi ^ {(1:\ell)} _ {2} \varphi ^ {(2:\ell)} _ {1} \right) \right|^2$ é a probabilidade (por unidade de área) de achar o sistema no estado tripleto.

O perfil da densidade de probabilidade $\left| \left( \varphi ^ {(1:\ell)} _ {1} \varphi ^ {(2:\ell)} _ {2} - \varphi ^ {(1:\ell)} _ {2} \varphi ^ {(2:\ell)} _ {1} \right) \right|^2$ é apresentado na Figura 6.1: O elétron $(1)$ não ocupa o mesmo espaço do elétron $(2)$, ocupa um espaço distânte.

Ao anexar o spin ao caso dos elétrons que não possuem a mesma energia $(n=1, \eta=2)$, o elétron $(1)$, na posição $x^{(1)}$, se acopla (via spin) com elétron $(2)$, na posição $x^{(2)} \ne x^{(1)}$, e formam um sistema com spin total 1:

$\hspace{2cm}$ — O elétron $(1)$, com o mesmo spin do outro, não ocupa o mesmo espaço do outro, se distancia do outro.

Referências

Robinett, R W. 2006. Quantum Mechanics: Classical Results, Modern Systems, and Visualized Examples. 2nd ed. Oxford University Press , ISBN 978-0-19-853097-8.

Zettili, N. 2009. Quantum Mechanics Concepts and Applications. 2nd ed. John Wiley; Sons, Ltd. , ISBN 978-0-470-02678-6.

Poço quântico

Cássio Sanguini Sergio

Físico

Meus interesses de pesquisa incluem aglomerados e semicondutores.