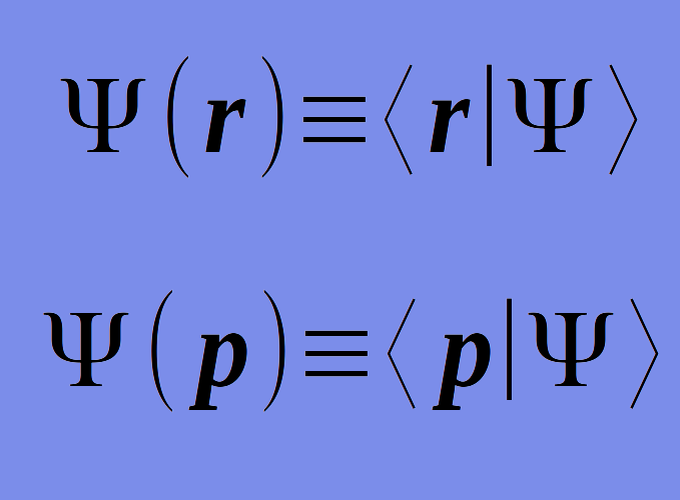1 Introdução
A função de onda e o vetor matricial são duas representações dos vetores de estado no espaço de Hilbert, ou dos vetores associados a observáveis. Foram introduzidas por Schödinger e Heisenberg, respectivamente.
A função de onda faz parte do que é chamado de mecânica ondulatória, e o vetor matricial, do que é chamado de mecânica matricial.
A origem da diferença está na base que se escolhe para representar o vetor de estado. Uma base contínua dá origem à função de onda e uma base discreta, ao vetor matricial.
O objetivo deste artigo é tratar das representações de vetores no espaço de Hilbert. O texto se fundamenta no livro (Zettili 2009).
2 A linguagem na notação de Dirac
A linguagem da mecânica quântica na notação de Dirac é apresentada nos exemplos abaixo, ademais, em alguns casos, entre parênteses há o correspondente em inglês.
Exemplo de …
… ket ou vetor de estado (state vector): \(\left| a \right\rangle\).
… bra ou vetor de estado dual (dual state vector): \(\left\langle a \right|\).
… bra-ket ou produto interno (inner product) ou produto escalar (scalar product): \(\left\langle a \middle| b \right\rangle=\left\langle b \middle| a \right\rangle^{\ast}\).
Nota: O resultado do produto escalar é um número complexo.
… norma (norm) de um ket: \(\left\langle a \middle| a \right\rangle\).
Nota: O resultado da norma é um número real e positivo, ademais, se o resultado for igual a 1, o ket está normalizado; então, \(\left| a \right\rangle\) está normalizado se \(\left\langle a \middle| a \right\rangle=1\).
… operador “prensado” (the operator is sandwiched between a bra and a ket): \(\left\langle a \middle| A \middle| b \right\rangle\).
… valor esperado (expectation value) ou valor médio (mean value): \(\left\langle A \right\rangle=\dfrac{\left\langle a \middle| A \middle| a \right\rangle} {\left\langle a \middle| a \right\rangle}\).
Nota: Se \(\left| a \right\rangle\) está normalizado \(\left\langle A \right\rangle=\left\langle a \middle| A \middle| a \right\rangle\).
… um ket com um número real (constante de Planck): \(\left| \hbar a \right\rangle=\hbar \left| a \right\rangle\).
… um bra com um número real: \(\left\langle \hbar a \right|=\hbar \left\langle a \right|\).
… um ket com um número complexo representado por \(\alpha\): \(\left| \alpha a \right\rangle=\alpha \left| a \right\rangle\).
… um bra com um número complexo: \(\left\langle \alpha a \right|=\alpha^{\ast} \left\langle a \right|\).
… kets ortogonais: \(\left\langle a \middle| b \right\rangle=0\).
… kets ortonormais: \(\left\langle a \middle| b \right\rangle=0\), ademais, \(\left\langle a \middle| a \right\rangle=1\) e \(\left\langle b \middle| b \right\rangle=1\).
… algebra com ket: \(\left| a+b \right\rangle=\left| a \right\rangle+\left| b \right\rangle\).
… algebra com bra: \(\left\langle a+b \right|=\left\langle a \right|+\left\langle b \right|\).
… algebra com bra-ket: \(\left\langle a+b \middle| a+b \right\rangle =\left\langle a \middle| a \right\rangle +\left\langle a \middle| b \right\rangle +\left\langle b \middle| a \right\rangle +\left\langle b \middle| b \right\rangle\).
… operador ket-bra: \(\left| a \right\rangle\left\langle b \right|\).
Nota: O produto bra-ket \(\left\langle a \middle| b \right\rangle\) resulta em um número complexo, por isso do nome produto escalar, por outro lado, o produto ket-bra \(\left| a \right\rangle\left\langle b \right|\) é um operador que atual em um ket para gerar outro ket: \((\left| a \right\rangle\left\langle b \right|) \left| c \right\rangle=\left\langle b \middle| c \right\rangle \left| a \right\rangle\); por causa de \(\left\langle b \middle| c \right\rangle\) ser um número complexo, gera-se o ket \(\left| a \right\rangle\).
… certo operador \(C\) que atua em um ket para gerar outro ket: \(C\left| a \right\rangle=\left| b \right\rangle\).
… operador que atua em um ket para gerar outro ket que é multiplo do ket de partida: \(A\left| a \right\rangle=a\left| a \right\rangle\).
Nota: A equação \(A\left| a_n \right\rangle=a_n\left| a_n \right\rangle\) é chamada equação de autovalor de \(A\), pois \(a_n\) são os autovalores (eigenvalues) de \(A\). Também pode ser denominada equação de autovetor de \(A\), pois \(\left| a_n \right\rangle\) são os autovetores (eigenvectors) de \(A\). Para um operador geral, os autovalores são números complexos, mas, para um operador Hermitiano (Hermitian), se \(A=A^{\dagger}\), os autovalores são números reais e os autovetores correspondentes a diferentes autovalores são ortogonais, além disso, os autovetores são ortonormais, \(\left\langle a_m \middle| a_n \right\rangle=\delta _{mn}\), e formam a base de \(A\): \(\{\left| a_n \right\rangle, n=1,2,3,\dots\}\). A base de \(A\) também manifesta completude: \(\sum _ {n} \left| a_n \right\rangle \left\langle a_n \right| = \hat{1}\), onde \(\hat{1}\) é o operador de unidade ou identidade.
3 Vetores no espaço Euclidiano
O vetor que possue módulo, direção e sentido é um vetor do espaço Euclidiano. Dizer que é do espaço Euclidiano significa dizer que ele obedece regras e operações matemáticas específicas, como, por exemplo, ele se permite somar com um outro vetor desse mesmo espaço, se multiplicar com um escalar, se multiplicar com um outro vetor (através do produto escalar e do produto vetorial), e assim por diante. Dizer que ele é do espaço Euclidiano também significa dizer que ele pode ser expresso em termos de outros vetores multuamente ortonormais desse mesmo espaço. Ao grupo de vetores multuamente ortonormais dá-se o nome de base, e a um vetor específico dessa base, dá-se o nome de vetor de base. Então, dizer que um vetor pode ser expresso em termos de outros vetores, significa dizer que ele pode ser expresso em termos de vetores de base, ou, alternadamente, significa dizer que ele pode ser expandido em certa base do espaço Euclidiano. As bases mais famosas do espaço Euclidiano são as bases formadas pelos vetores de base cartesianos \(( \mathbf{e} _{x}, \mathbf{e} _{y}, \mathbf{e} _{z})\) e pelos vetores de base polares \(( \mathbf{e} _{r}, \mathbf{e} _{\theta}, \mathbf{e} _{\phi})\).
Um vetor expresso em termos dos vetores de base cartesianos é um vetor expresso como:
\[\begin{equation} \mathbf{V} = V _ {x} \mathbf{e} _ {x} + V _ {y} \mathbf{e} _ {y} + V _ {z} \mathbf{e} _ {z} . \label{eq:R1a} \end{equation}\]
Agora, o mesmo vetor expresso em termos dos vetores de base polares é expresso como:
\[\begin{equation} \mathbf{V} = V _ {r} \mathbf{e} _ {r} + V _ {\theta} \mathbf{e} _ {\theta} + V _ {\phi} \mathbf{e} _ {\phi} . \label{eq:R1b} \end{equation}\]
Então, a representação de \( \mathbf{V} \) na base cartesiana é:
\[\begin{equation} \left( V _ {x}\ ,\ V _ {y}\ ,\ V _ {z} \right) = \left( \mathbf{e} _ {x} \cdot \mathbf{V} \ ,\ \mathbf{e} _ {y} \cdot \mathbf{V} \ ,\ \mathbf{e} _ {z} \cdot \mathbf{V} \right) , \label{eq:R2a} \end{equation}\]
e a representação de \( \mathbf{V} \) na base polar é:
\[\begin{equation} \newcommand{\vv}[1]{ \mathbf{#1} } \left( V _ {r}\ ,\ V _ {\theta}\ ,\ V _ {\phi} \right) = \left( \mathbf{e} _ {r} \cdot \mathbf{V} \ ,\ \mathbf{e} _ {\theta} \cdot \mathbf{V} \ ,\ \mathbf{e} _ {\phi} \cdot \mathbf{V} \right) . \label{eq:R2b} \end{equation}\]
Inspecionando \(\eqref{eq:R2a}\) e \(\eqref{eq:R2b}\), conclui-se que \( \mathbf{V} \) pode ser representado por suas componentes cartesianas \(\left( V _ {x} , V _ {y} , V _ {z} \right)\) ou por suas componentes polares \(\left( V _ {r} , V _ {\theta} , V _ {\phi} \right)\). Esta conclusão abre a questão:
Como transformar um vetor de uma base para outra? Conhecendo as componentes de um vetor na base cartesiana, como fazer para saber as componentes desse vetor na base polar? Basta expressar a base cartesiana em termos da base polar:
\[\begin{equation} \begin{aligned} \mathbf{e} _ {x} &= U _ {rx} \mathbf{e} _ {r} + U _ {\theta x} \mathbf{e} _ {\theta} + U _ {\phi x} \mathbf{e} _ {\phi} ,\notag\\ \mathbf{e} _ {y} &= U _ {ry} \mathbf{e} _ {r} + U _ {\theta y} \mathbf{e} _ {\theta} + U _ {\phi y} \mathbf{e} _ {\phi} ,\notag\\ \mathbf{e} _ {z} &= U _ {rz} \mathbf{e} _ {r} + U _ {\theta z} \mathbf{e} _ {\theta} + U _ {\phi z} \mathbf{e} _ {\phi} ,\notag \end{aligned} \label{eq:R3a} \end{equation}\]
sendo,
\[\begin{equation} \begin{aligned} U _ {r x} &= \mathbf{e} _ {r} \cdot \mathbf{e} _ {x} ,\hspace{1cm} U _ {\theta x} = \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {x} ,\hspace{1cm} U _ {\phi x} = \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {x} ,\notag\\ U _ {r y} &= \mathbf{e} _ {r} \cdot \mathbf{e} _ {y} ,\hspace{1cm} U _ {\theta y} = \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {y} ,\hspace{1cm} U _ {\phi y} = \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {y} ,\notag\\ U _ {r z} &= \mathbf{e} _ {r} \cdot \mathbf{e} _ {z} ,\hspace{1cm} U _ {\theta z} = \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {z} ,\hspace{1cm} U _ {\phi z} = \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {z} .\notag \end{aligned} \label{eq:R3b} \end{equation}\]
Pode-se agrupar \(\eqref{eq:R3b}\) em uma matriz que recebe o nome de matriz de transformação. Importa, a ordem de se escrever a matriz de trasformação: na primeira linha, coloca-se os elementos \( \mathbf{e} _ {r} \cdot \mathbf{e} _ {i}\); na segunda linha, os elementos \( \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {i}\); e na terceira linha, os elementos \( \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {i}\):
\[\begin{equation} U = \begin{bmatrix} U _ {r x} & U _ {r y} & U _ {r z} \\ U _ {\theta x} & U _ {\theta y} & U _ {\theta z} \\ U _ {\phi x} & U _ {\phi y} & U _ {\phi z} \end{bmatrix} = \begin{bmatrix} \mathbf{e} _ {r} \cdot \mathbf{e} _ {x} & \mathbf{e} _ {r} \cdot \mathbf{e} _ {y} & \mathbf{e} _ {r} \cdot \mathbf{e} _ {z}\\ \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {x} & \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {y} & \mathbf{e} _ {\theta} \cdot \mathbf{e} _ {z}\\ \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {x} & \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {y} & \mathbf{e} _ {\phi} \cdot \mathbf{e} _ {z} \end{bmatrix} . \label{eq:R3c} \end{equation}\]
Enfim, a transformação é feita assim:
\[\begin{equation} \mathbf{V} _ {r \theta \phi} = U\ \mathbf{V} _ {xyz} . \label{eq:R4a} \end{equation}\]
Na forma matricial, \(\eqref{eq:R4a}\) tem o aspecto:
\[\begin{equation} \begin{bmatrix} V _ {r} \\ V _ {\theta} \\ V _ {\phi} \end{bmatrix} = \begin{bmatrix} U _ {r x} & U _ {r y} & U _ {r z} \\ U _ {\theta x} & U _ {\theta y} & U _ {\theta z} \\ U _ {\phi x} & U _ {\phi y} & U _ {\phi z} \end{bmatrix} \begin{bmatrix} V _ {x} \\ V _ {y} \\ V _ {z} \end{bmatrix} . \label{eq:R4b} \end{equation}\]
4 Vetores no espaço de Hilbert
Os vetores associados a observáveis são vetores do espaço de Hilbert. Pode-se dar como exemplos, o vetor de energia, o vetor de momento linear, o vetor de momento angular, o vetor de spin, etc. Dizer que são do espaço de Hilbert significa dizer que eles satisfazem as regras do espaço de Hilbert . As principais regras são:
– da adição: \(\left| c \right\rangle=\left| a \right\rangle+\left| b \right\rangle\);
– da multiplicação por um escalar: \(\left| b \right\rangle=\alpha\left| a \right\rangle\);
– do produto escalar: \(\alpha=\left\langle a \middle| b \right\rangle\).
As regras do espaço de Hilbert permitem a construção de bases para se expressar vetores. Uma base ortonormal é formada por autovetores de um operador Hermitiano. Sendo \(A\) e \(B\) operadores Hermitianos, considere a base discreta e ortonormal \(\{\left| a_n \right\rangle, n=1,2,3,\dots\}\), da operação \(A\left| a_n \right\rangle=a_n\left| a_n \right\rangle\), também, considere a base discreta e ortonormal \(\{\left| b_n \right\rangle\}\), da operação \(B\left| b_n \right\rangle=b_n\left| b_n \right\rangle\). Certo vetor \(\left| c \right\rangle\) pode ser expresso nessas bases:
\[\begin{equation} \begin{aligned} \left| c \right\rangle &= \sum _ {n} \alpha _ {n} \left| a _ n \right\rangle , \notag\\ \left| c \right\rangle &= \sum _ {n} \beta _ {n} \left| b _ n \right\rangle . \notag \end{aligned} \label{eq:R5a} \end{equation}\]
O coeficiente \(\alpha_n\) é amplitude de probabilidade. Dizer que \(\alpha_n\) é amplitude de probabilidade significa dizer que \(|\alpha_n|^2\) é a probabilidade do estado \(\left| c \right\rangle\) colapsar no estado \(\left| a _ n \right\rangle\). \(\beta_n\) cumpre o mesmo papel, mas, agora, \(\left| c \right\rangle\) colapsa em um outro estado, no \(\left| b _ n \right\rangle\), com a probabilidade \(|\beta_n|^2\).
Inspecionando \(\eqref{eq:R5a}\), conclui-se que \(\left| c \right\rangle\) é representado pelas componentes \(\alpha_n = \left\langle a_n \middle| c \right\rangle\), quando expresso na base \(\{\left| a_n \right\rangle\}\), e representado pelas componentes \(\beta_n = \left\langle b_n \middle| c \right\rangle\), quando expresso na base \(\{\left| b_n \right\rangle\}\).
O vetor \(\left| c \right\rangle\) é um vetor matricial, então, nas bases discretas \(\{\left| a_n \right\rangle\}\) e \(\{\left| b_n \right\rangle\}\), ele tem os aspectos:
\[\begin{equation} \left| c \right\rangle = \begin{bmatrix} \alpha _ 1 \\ \alpha _ 2 \\ \alpha _ 3 \\ \vdots \end{bmatrix} , \label{eq:R5b} \end{equation}\]
\[\begin{equation} \left| c \right\rangle = \begin{bmatrix} \beta _ 1 \\ \beta _ 2 \\ \beta _ 3 \\ \vdots \end{bmatrix} . \label{eq:R5c} \end{equation}\]
Reforçando o conceito, \(\eqref{eq:R5b}\) é a representação matricial de \(\left| c \right\rangle\) na base \(\{\left| a_n \right\rangle\}\), e \(\eqref{eq:R5c}\) é a representação matricial de \(\left| c \right\rangle\) na base \(\{\left| b_n \right\rangle\}\). Esta observação abre a questão:
Como transformar \(\left| c \right\rangle\) de uma base para outra? Conhecendo as componentes de \(\left| c \right\rangle\) na base \(\{\left| a_n \right\rangle\}\), como fazer para saber as componentes desse vetor na base \(\{\left| b_n \right\rangle\}\)? Basta expressar a base \(\{\left| a_n \right\rangle\}\) em termos da base \(\{\left| b_n \right\rangle\}\):
\[\begin{equation} \begin{aligned} \newcommand{\ket}[1]{\left| #1 \right\rangle} \left| a _ 1 \right\rangle&=U _ {11} \left| b _ 1 \right\rangle +U _ {21} \left| b _ 2 \right\rangle +U _ {31} \left| b _ 3 \right\rangle +\cdots ,\notag\\ \left| a _ 2 \right\rangle&=U _ {12} \left| b _ 1 \right\rangle +U _ {22} \left| b _ 2 \right\rangle +U _ {32} \left| b _ 3 \right\rangle +\cdots ,\notag\\ \left| a _ 3 \right\rangle&=U _ {13} \left| b _ 1 \right\rangle +U _ {23} \left| b _ 2 \right\rangle +U _ {33} \left| b _ 3 \right\rangle +\cdots ,\notag\\ & \hspace{0.25cm} \vdots \notag \end{aligned} \label{eq:R6} \end{equation}\]
sendo,
\[\begin{equation} \begin{aligned} U _ {1 1} &= \left\langle b _ 1 \middle| a _ 1 \right\rangle ,\hspace{1cm} U _ {2 1} = \left\langle b _ 2 \middle| a _ 1 \right\rangle ,\hspace{1cm} U _ {3 1} = \left\langle b _ 3 \middle| a _ 1 \right\rangle ,\hspace{1cm} \cdots \notag\\ U _ {1 2} &= \left\langle b _ 1 \middle| a _ 2 \right\rangle ,\hspace{1cm} U _ {2 2} = \left\langle b _ 2 \middle| a _ 2 \right\rangle ,\hspace{1cm} U _ {3 2} = \left\langle b _ 3 \middle| a _ 2 \right\rangle ,\hspace{1cm} \cdots \notag\\ U _ {1 3} &= \left\langle b _ 1 \middle| a _ 3 \right\rangle ,\hspace{1cm} U _ {2 3} = \left\langle b _ 2 \middle| a _ 3 \right\rangle ,\hspace{1cm} U _ {3 3} = \left\langle b _ 3 \middle| a _ 3 \right\rangle ,\hspace{1cm} \cdots \notag\\ & \hspace{0.25cm} \vdots \notag \end{aligned} \label{eq:R7} \end{equation}\]
ou, considerando \(m\) e \(n\) números inteiros, \(U_{mn}=\left\langle b_m \middle| a_n \right\rangle\).
A matriz de trasformação é construída organizando \(\eqref{eq:R7}\): na primeira linha, coloca-se os elementos \(\left\langle b_1 \middle| a_n \right\rangle\); na segunda linha, os elementos \(\left\langle b_2 \middle| a_n \right\rangle\); na terceira linha, os elementos \(\left\langle b_3 \middle| a_n \right\rangle\); a assim por diante:
\[\begin{equation} U = \begin{bmatrix} U _ {1 1} & U _ {1 2} & U _ {1 3} & \cdots \\ U _ {2 1} & U _ {2 2} & U _ {2 3} & \cdots \\ U _ {3 1} & U _ {3 2} & U _ {3 3} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} . \label{eq:R9} \end{equation}\]
Enfim, a transformação é feita assim:
\[\begin{equation} \left| c _ \beta \right\rangle = U \left| c _ \alpha \right\rangle . \label{eq:R10a} \end{equation}\]
Na forma matricial, \(\eqref{eq:R10a}\) tem o aspecto:
\[\begin{equation} \begin{bmatrix} \beta _ 1 \\ \beta _ 2 \\ \beta _ 3 \\ \vdots \end{bmatrix} = \begin{bmatrix} U _ {1 1} & U _ {1 2} & U _ {1 3} & \cdots \\ U _ {2 1} & U _ {2 2} & U _ {2 3} & \cdots \\ U _ {3 1} & U _ {3 2} & U _ {3 3} & \cdots \\ \vdots & \vdots & \vdots & \ddots \end{bmatrix} \begin{bmatrix} \alpha _ 1 \\ \alpha _ 2 \\ \alpha _ 3 \\ \vdots \end{bmatrix} . \label{eq:R10b} \end{equation}\]
Examinamdo \(\eqref{eq:R10b}\), a forma compacta da transformação é:
\[\begin{equation} \beta _ {m} = \sum _ {n} U _ {mn} \alpha _ {n} . \label{eq:R10c} \end{equation}\]
5 E se a base for contínua?
Vamos continuar representando vetores no espaço de Hilbert, mas, agora, trabalharemos com bases contínuas.
A linguagem de base discreta será adptada à linguagem de base contínua.
As bases \(\{\left| a_n \right\rangle\}\) e \(\{\left| b_n \right\rangle\}\) são discretas: \(n\) é um parâmetro inteiro.
As bases \(\{\left| a_k \right\rangle\}\) e \(\{\left| b_k \right\rangle\}\) são contínuas: \(k\) é um parâmetro contínuo.
A condição de ortonormalidade da base discreta \(\{\left| a_n \right\rangle\}\) é expressa pelo delta de Kronecker: \(\left\langle a_m \middle| a_n \right\rangle=\delta _{mn}\).
A condição de ortonormalidade da base contínua \(\{\left| a_k \right\rangle\}\) é expressa pelo delta de Dirac: \(\left\langle a_p \middle| a_k \right\rangle=\delta(k-p)\).
Para expressar um vetor em uma base contínua, temos que substituir a somatória em \(n\) pela integral em \(k\). Nas bases contínuas \(\{\left| a_k \right\rangle\}\) e \(\{\left| b_k \right\rangle\}\), certo vetor \(\left| c \right\rangle\) fica assim representado:
\[\begin{equation} \begin{aligned} \left| c \right\rangle &= \int _ {-\infty}^{+\infty}dk\ \ \alpha(k) \left| a _ k \right\rangle , \notag\\ \left| c \right\rangle &= \int _ {-\infty}^{+\infty}dk\ \ \beta(k) \left| b _ k \right\rangle . \\ \end{aligned} \label{eq:R11} \end{equation}\]
O coeficiente \(\alpha(k)\) é a amplitude de probabilidade em \(k\). Dizer que \(\alpha(k)\) é a amplitude de probabilidade em \(k\) significa dizer que \(|\alpha(k)|^2 dk\) é a probabilidade do estado \(\left| c \right\rangle\) colapsar entre os estados \(\left| a_k \right\rangle\) e \(\left| a_{k+dk} \right\rangle\). \(\beta_n\) cumpre o mesmo papel, mas, agora, \(\left| c \right\rangle\) colapsa entre os estados \(\left| b_k \right\rangle\) e \(\left| b_{k+dk} \right\rangle\), tendo probabilidade \(|\beta(k)|^2 dk\) disso acontecer.
Inspecionando \(\eqref{eq:R11}\), conclui-se que \(\left| c \right\rangle\) é representado pelas componentes \(\alpha(k) = \left\langle a_k \middle| c \right\rangle\), quando expresso na base \(\{\left| a_k \right\rangle\}\), e representado pelas componentes \(\beta(k)= \left\langle b_k \middle| c \right\rangle\), quando expresso na base \(\{\left| b_k \right\rangle\}\). Reforçando o conceito, \(\alpha(k)\) e \(\beta(k)\) são as componentes contínuas de \(\left| c \right\rangle\) que fazem o mesmo papel das componentes de um vetor Euclidiano: representar um vetor quando esse vetor é expresso em uma base.
Os conceitos ficarão mais claros quando abandonarmos a linguagem genérica e partirmos para a linguagem específica. Por isso, vamos especificar duas bases contínuas: a base de posição e a base de momento linear.
5.1 A base de posição
A base de posição é formada por autovetores do operador de posição. Operador de posição \( \mathbf{R} \) é um operador vetorial:
\[\begin{equation} \mathbf{R} = X \mathbf{e} _ {x} + Y \mathbf{e} _ {y} + Z \mathbf{e} _ {z} . \label{eq:R12} \end{equation}\]
As componentes cartesianas do operador de posição são os operadores \(X\), \(Y\) e \(Z\).
Os autovetores de posição \(\left| \mathbf{r} \right\rangle\) e os autovalores de posição \( \mathbf{r} \) são os resultados da operação:
\[\begin{equation} \mathbf{R} \left| \mathbf{r} \right\rangle = \mathbf{r} \left| \mathbf{r} \right\rangle . \label{eq:R13} \end{equation}\]
Os autovalores de posição são os vetores tradicionais que posicionam um objeto no espaço tridimencional:
\[\begin{equation} \mathbf{r} = x \mathbf{e} _ {x} + y \mathbf{e} _ {y} + z \mathbf{e} _ {z} . \label{eq:R14} \end{equation}\]
De acordo com \(\eqref{eq:R14}\), a posição de um objeto pelo espaço em que vivemos é \((x,y,z)\).
Voltando a falar sobre a base de posição, vemos que ela surge de \(\eqref{eq:R13}\). A base \(\{ \left| \mathbf{r} \right\rangle \}\) é uma base contínua que se caracteriza por ser ortonormal:
\[\begin{equation} \left\langle \mathbf{r} ' \middle| \mathbf{r} \right\rangle = \delta ( \mathbf{r} - \mathbf{r} ') , \label{eq:R15a} \end{equation}\]
e possuir completude:
\[\begin{equation} \int d^3r\ \ \left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \right| = \hat{1} , \label{eq:R15b} \end{equation}\]
onde \(\hat{1}\) é o operador de unidade ou identidade.
Considere \(\left| \Psi \right\rangle\) um vetor do espaço de Hilbert, e considere escrevê-lo na forma:
\[\begin{equation} \left| \Psi \right\rangle = \hat{1} \left| \Psi \right\rangle . \label{eq:R16} \end{equation}\]
Substituindo \(\eqref{eq:R15b}\) em \(\eqref{eq:R16}\):
\[\begin{equation} \left| \Psi \right\rangle = \int d^3r\ \ \left| \mathbf{r} \right\rangle \left\langle \mathbf{r} \middle| \Psi \right\rangle . \label{eq:R17a} \end{equation}\]
Vamos escrever \(\eqref{eq:R17a}\) de uma maneira mais amigável:
\[\begin{equation} \left| \Psi \right\rangle = \int d^3r\ \ \left\langle \mathbf{r} \middle| \Psi \right\rangle \left| \mathbf{r} \right\rangle . \label{eq:R17b} \end{equation}\]
Agora me façam um favor: comparem cuidadosamente \(\eqref{eq:R17b}\) com \(\eqref{eq:R11}\). Conseguem enxergar o que eu enxergo?
Sim, \(\left\langle \mathbf{r} \middle| \Psi \right\rangle\) é amplitude de probabilidade!
Sim, \(\left\langle \mathbf{r} \middle| \Psi \right\rangle\) são as componentes do vetor \(\left| \Psi \right\rangle\)!
E a equação \(\eqref{eq:R17b}\) é a equação do vetor \(\left| \Psi \right\rangle\) expresso na base \(\{ \left| \mathbf{r} \right\rangle \}\).
Usando o fato que um vetor pode ser representado por suas componentes, outra maneira de interpretar \(\left\langle \mathbf{r} \middle| \Psi \right\rangle\) é dizer que \(\left\langle \mathbf{r} \middle| \Psi \right\rangle\) é a representação de posição do vetor \(\left| \Psi \right\rangle\).
A representação de posição de um vetor recebe um nome e atenção especial na teoria ondulatória da mecânica quântica.
A representação de posição do vetor \(\left| \Psi \right\rangle\) é a função de onda desse vetor:
\[\begin{equation} \left\langle \mathbf{r} \middle| \Psi \right\rangle \equiv \Psi( \mathbf{r} ) . \label{eq:R18a} \end{equation}\]
(Invertendo.)
A função de onda do vetor \(\left| \Psi \right\rangle\) é a representação de posição desse vetor:
\[\begin{equation} \Psi( \mathbf{r} ) \equiv \left\langle \mathbf{r} \middle| \Psi \right\rangle . \label{eq:R18b} \end{equation}\]
A equivalência \(\eqref{eq:R18b}\) indica o significado probabilístico da função de onda:
A função de onda na posição \( \mathbf{r} \) é a amplitude de probabilidade na posição \( \mathbf{r} \).
Outra maneira de interpretar \(\eqref{eq:R18b}\) é escrevâ-la na forma:
\[\begin{equation} |\Psi( \mathbf{r} )|^2 d^3r \equiv |\left\langle \mathbf{r} \middle| \Psi \right\rangle|^2 d^3r . \label{eq:R19} \end{equation}\]
A equivalência \(\eqref{eq:R19}\) indica:
A probabilidade de se ocupar uma das posições \( \mathbf{r} \) do volume elementar \(d^3r\) é a probabilidade do estado \(\left| \Psi \right\rangle\) colapsar em um dos estados \(\left| \mathbf{r} \right\rangle\) que pertencem a esse volume.
5.2 A base de momento linear
A base de momento é formada por autovetores do operador de momento. Operador de momento \( \mathbf{P} \) é um operador vetorial:
\[\begin{equation} \mathbf{P} = P _ x \mathbf{e} _ {x} + P _ y \mathbf{e} _ {y} + P _ z \mathbf{e} _ {z} . \label{eq:R12m} \end{equation}\]
As componentes cartesianas do operador de momento são os operadores \(P_x\), \(P_y\) e \(P_z\).
Os autovetores de momento \(\left| \mathbf{p} \right\rangle\) e os autovalores de momento \( \mathbf{p} \) são os resultados da operação:
\[\begin{equation} \mathbf{P} \left| \mathbf{p} \right\rangle = \mathbf{p} \left| \mathbf{p} \right\rangle . \label{eq:R13m} \end{equation}\]
Os autovalores de momento são os momentos tradicionais que descrevem um objeto em movimento pelo espaço tridimencional:
\[\begin{equation} \newcommand{\vv}[1]{ \mathbf{#1} } \mathbf{p} = p _ x \mathbf{e} _ {x} + p _ y \mathbf{e} _ {y} + p _ z \mathbf{e} _ {z} . \label{eq:R14m} \end{equation}\]
De acordo com \(\eqref{eq:R14m}\), o momento de um objeto pelo espaço em que vivemos é \((p_x,p_y,p_z)\).
Voltando a falar sobre a base de momento, vemos que ela surge de \(\eqref{eq:R13m}\). A base \(\{ \left| \mathbf{p} \right\rangle \}\) é uma base contínua que se caracteriza por ser ortonormal:
\[\begin{equation} \left\langle \mathbf{p} ' \middle| \mathbf{p} \right\rangle = \delta ( \mathbf{p} - \mathbf{p} ') , \label{eq:R15am} \end{equation}\]
e possuir completude:
\[\begin{equation} \int d^3p\ \ \left| \mathbf{p} \right\rangle \left\langle \mathbf{p} \right| = \hat{1} . \label{eq:R15bm} \end{equation}\]
Considere \(\left| \Psi \right\rangle\) o mesmo vetor do espaço de Hilbert da seção anterior [ seção 5.1 ], mas agora considere escrevê-lo com \(\eqref{eq:R15bm}\):
\[\begin{equation} \left| \Psi \right\rangle = \hat{1} \left| \Psi \right\rangle , \label{eq:R16m} \end{equation}\]
o que resulta em:
\[\begin{equation} \left| \Psi \right\rangle = \int d^3p\ \ \left| \mathbf{p} \right\rangle \left\langle \mathbf{p} \middle| \Psi \right\rangle . \label{eq:R17am} \end{equation}\]
Vamos escrever \(\eqref{eq:R17am}\) de uma maneira mais amigável:
\[\begin{equation} \left| \Psi \right\rangle = \int d^3p\ \ \left\langle \mathbf{p} \middle| \Psi \right\rangle \left| \mathbf{p} \right\rangle . \label{eq:R17bm} \end{equation}\]
Agora me façam outro favor: comparem \(\eqref{eq:R17bm}\) com \(\eqref{eq:R11}\).
Sim, \(\left\langle \mathbf{p} \middle| \Psi \right\rangle\) é amplitude de probabilidade!
Sim, \(\left\langle \mathbf{p} \middle| \Psi \right\rangle\) são as componentes do vetor \(\left| \Psi \right\rangle\)!
E a equação \(\eqref{eq:R17bm}\) é a equação do vetor \(\left| \Psi \right\rangle\) expresso na base \(\{ \left| \mathbf{p} \right\rangle \}\).
Usando o fato que um vetor pode ser representado por suas componentes, outra maneira de interpretar \(\left\langle \mathbf{p} \middle| \Psi \right\rangle\) é dizer que \(\left\langle \mathbf{p} \middle| \Psi \right\rangle\) é a representação de momento do vetor \(\left| \Psi \right\rangle\).
A representação de momento de um vetor recebe um nome e atenção especial na teoria ondulatória da mecânica quântica.
A representação de momento do vetor \(\left| \Psi \right\rangle\) é a função de onda desse vetor:
\[\begin{equation} \left\langle \mathbf{p} \middle| \Psi \right\rangle \equiv \Psi( \mathbf{p} ) . \label{eq:R18am} \end{equation}\]
(Invertendo.)
A função de onda do vetor \(\left| \Psi \right\rangle\) é a representação de momento desse vetor:
\[\begin{equation} \Psi( \mathbf{p} ) \equiv \left\langle \mathbf{p} \middle| \Psi \right\rangle . \label{eq:R18bm} \end{equation}\]
A equivalência \(\eqref{eq:R18bm}\) indica o significado probabilístico da função de onda:
A função de onda no momento \( \mathbf{p} \) é a amplitude de probabilidade no momento \( \mathbf{p} \).
Outra maneira de interpretar \(\eqref{eq:R18bm}\) é escrevâ-la na forma:
\[\begin{equation} |\Psi( \mathbf{p} )|^2 d^3p \equiv |\left\langle \mathbf{p} \middle| \Psi \right\rangle|^2 d^3p . \label{eq:R19m} \end{equation}\]
A equivalência \(\eqref{eq:R19m}\) indica:
A probabilidade de se ocupar um dos momentos \( \mathbf{p} \) do volume elementar \(d^3p\) é a probabilidade do estado \(\left| \Psi \right\rangle\) colapsar em um dos estados \(\left| \mathbf{p} \right\rangle\) que pertencem a esse volume.
OBSERVAÇÃO:
A seção anterior é somente sobre posição e esta somente sobre momento, por isso, não se fez necessário dar complemento à nomenclatura “função de onda.” Todavia, quando as 2 funções estão no mesmo contexto, é preciso escrever:
Função de onda no espaço de posição para \(\Psi( \mathbf{r} )\) e função de onda no espaço de momento para \(\Psi( \mathbf{p} )\).
5.3 Da base de posição para a base de momento
Na [ seção 5.1 ] escrevemos \(\left| \Psi \right\rangle\) na base de posição e na [ seção 5.2 ] escrevemos esse mesmo vetor na base de momento:
\[\begin{equation} \left| \Psi \right\rangle = \int d^3r\ \Psi( \mathbf{r} ) \left| \mathbf{r} \right\rangle , \label{eq:R50a} \end{equation}\]
\[\begin{equation} \left| \Psi \right\rangle = \int d^3p\ \Psi( \mathbf{p} ) \left| \mathbf{p} \right\rangle . \label{eq:R50b} \end{equation}\]
Como transformar \(\left| \Psi \right\rangle\) de uma base para outra?
No caso das bases discretas [ seção 4 ], resolvemos a questão: Conhecendo as componentes do vetor \(\left| c \right\rangle\) na base \(\{\left| a_n \right\rangle\}\), como fazer para saber as componentes desse vetor na base \(\{\left| b_n \right\rangle\}\)?, expressando a base \(\{\left| a_n \right\rangle\}\) em termos da base \(\{\left| b_n \right\rangle\}\).
A questão agora é: Conhecendo as componentes do vetor \(\left| \Psi \right\rangle\) na base de posição \(\{\left| \mathbf{r} \right\rangle\}\), como fazer para saber as componentes desse vetor na base de momento \(\{\left| \mathbf{p} \right\rangle\}\)?
Bem, precisamos expressar a base \(\{ \left| \mathbf{r} \right\rangle \}\) em termos da base \(\{\left| \mathbf{p} \right\rangle\}\).
No caso das bases discretas, o aspecto da fórmula é:
\[\begin{equation} \left| a _ n \right\rangle = \sum _ {m} U _ {mn} \left| b _ m \right\rangle . \label{eq:R51} \end{equation}\]
Por analogia, poderíamos pensar em algo assim:
\[\begin{equation} \left| \mathbf{r} \right\rangle = \sum U _ {[ \mathbf{p} \gets \mathbf{r} ]} \left| \mathbf{p} \right\rangle . \label{eq:R52} \end{equation}\]
Todavia, deve-se usar integral ao invés de somatória:
\[\begin{equation} \left| \mathbf{r} \right\rangle = \int d^3p\ U _ {[ \mathbf{p} \gets \mathbf{r} ]} \left| \mathbf{p} \right\rangle . \label{eq:R53} \end{equation}\]
A multiplicação da equação \(\eqref{eq:R53}\) por \(\left\langle \Psi \right|\) resulta em:
\[\begin{equation} \left\langle \Psi \middle| \mathbf{r} \right\rangle = \int d^3p\ \ U _ {[ \mathbf{p} \gets \mathbf{r} ]} \left\langle \Psi \middle| \mathbf{p} \right\rangle . \label{eq:R54} \end{equation}\]
Usando a propriedade \([ \Psi( \mathbf{r} ) ]^{\ast} = [ \left\langle \mathbf{r} \middle| \Psi \right\rangle ]^{\ast} = \left\langle \Psi \middle| \mathbf{r} \right\rangle\):
\[\begin{equation} \Psi^{\ast} ( \mathbf{r} ) = \int d^3p\ \ U _ {[ \mathbf{p} \gets \mathbf{r} ]} \Psi ^{\ast} ( \mathbf{p} ). \label{eq:R55} \end{equation}\]
A inspiração para se encontrar a expressão da função de transformação \([ \mathbf{p} \gets \mathbf{r} ]\) vem da transformada de Fourier. Segundo Fourier, a transformação [\( \mathbf{r} \gets \mathbf{p} \)] é:
\[\begin{equation} F( \mathbf{r} ) = (2\pi\hbar)^{-3/2} \int d^3p\ e^{i \mathbf{p} \cdot \mathbf{r} \hbar^{-1}} F( \mathbf{p} ) , \label{eq:R56} \end{equation}\]
então, dada a \(F\) no espaço de momento, determina-se a \(F\) no espaço de posição.
O complexo conjugado da equação de Fourier \(\eqref{eq:R56}\) é:
\[\begin{equation} F^{\ast} ( \mathbf{r} ) = \int d^3p\ e^{-i \mathbf{p} \cdot \mathbf{r} } F^{\ast} ( \mathbf{p} ) . \label{eq:R57} \end{equation}\]
A omissão das constantes \(\eqref{eq:R57b}\) é somente para simplificar a escrita gráfica. No final da dedução, voltamos com elas.
\[\begin{equation} (2\pi\hbar)^{-3/2} \ \ \ {\rm e} \ \ \ (\hbar)^{-1} . \label{eq:R57b} \end{equation}\]
A comparação da equação \(\eqref{eq:R57}\) com a \(\eqref{eq:R55}\) resulta na expressão da função de transformação [\( \mathbf{p} \gets \mathbf{r} \)]:
\[\begin{equation} U _ {[ \mathbf{p} \gets \mathbf{r} ]} = e^{-i \mathbf{p} \cdot \mathbf{r} } . \label{eq:R58} \end{equation}\]
Demos um passo importante para resolvermos a questão da transformação. Agora vamos procurar a fórmula da transformação. No caso das bases discretas, as componentes se trasnformam assim:
\[\begin{equation} \beta _ {m} = \sum _ {n} U _ {mn} \alpha _ {n} . \label{eq:R59a} \end{equation}\]
Então, por analogia, as componentes contínuas se trasformam desse jeito:
\[\begin{equation} \Psi ( \mathbf{p} ) = \int d^3r\ U _ {[ \mathbf{p} \gets \mathbf{r} ]} \Psi ( \mathbf{r} ). \label{eq:R59b} \end{equation}\]
Substituindo \(\eqref{eq:R58}\) em \(\eqref{eq:R59b}\), tem-se as componentes do vetor de estado na base de momento determinadas por meio das componentes desse vetor na base de posição:
\[\begin{equation} \Psi ( \mathbf{p} ) = \int d^3r\ e^{-i \mathbf{p} \cdot \mathbf{r} } \Psi ( \mathbf{r} ) . \label{eq:R60} \end{equation}\]
Outra maneira de expressar \(\eqref{eq:R60}\) é dizer que a função de onda no espaço de momento é determinada através da função de onda no espaço de posição.
\({ }\)
DEDUÇÃO COMPLEMENTAR:
Há uma maneira elegante de se determinar a função de onda no espaço de posição através da função de onda no espaço de momento.
Primeiro, fazemos o complexo conjugado da equação \(\eqref{eq:R55}\):
\[\begin{equation} \Psi ( \mathbf{r} ) = \int d^3p\ U _ {[ \mathbf{r} \gets \mathbf{p} ]} \Psi ( \mathbf{p} ). \label{eq:R70} \end{equation}\]
Em seguida, fazemos o complexo conjugado da equação \(\eqref{eq:R58}\):
\[\begin{equation} U _ {[ \mathbf{r} \gets \mathbf{p} ]} = e^{i \mathbf{p} \cdot \mathbf{r} } . \label{eq:R71} \end{equation}\]
Por fim, substituímos a função de transformação \(\eqref{eq:R71}\) na equação \(\eqref{eq:R70}\):
\[\begin{equation} \Psi ( \mathbf{r} ) = \int d^3p\ e^{i \mathbf{p} \cdot \mathbf{r} } \Psi ( \mathbf{p} ) . \label{eq:R72} \end{equation}\]
(Fim da dedução complementar.)
\({ }\)
— O quê falta?
A função de onda no espaço de posição \(\eqref{eq:R72}\) e a função de onda no espaço de momento \(\eqref{eq:R60}\) com a recondução das constantes \(\eqref{eq:R57b}\):
\[\begin{equation} \Psi ( \mathbf{r} ) = (2\pi\hbar)^{-3/2} \int d^3p\ e^{i \mathbf{p} \cdot \mathbf{r} \hbar^{-1}} \Psi ( \mathbf{p} ) , \label{eq:R100} \end{equation}\]
\[\begin{equation} \Psi ( \mathbf{p} ) = (2\pi\hbar)^{-3/2} \int d^3r\ e^{-i \mathbf{p} \cdot \mathbf{r} \hbar^{-1}} \Psi ( \mathbf{r} ) . \label{eq:R101} \end{equation}\]
5.4 Exemplos de funções de onda
Vamos aplicar as fórmulas \(\eqref{eq:R100}\) e \(\eqref{eq:R101}\) para determinar explicitamente algumas funções de onda nos espaços de posição e momento.
A notação será simplificada retirando-se novamente as constantes \(\eqref{eq:R57b}\) dessas fórmulas.
\(1^{\rm o}\) EXEMPLO:
Considere o vetor \(\left| \psi \right\rangle\) em certo estado de autovetor do operador de posição:
\[\begin{equation} \left| \psi \right\rangle = \left| \mathbf{r _ 0} \right\rangle . \label{eq:R200} \end{equation}\]
Agora considere esta matemática sobre \(\eqref{eq:R200}\):
\[\begin{equation} \left\langle \mathbf{r _ 0} \middle| \psi \right\rangle = \left\langle \mathbf{r _ 0} \middle| \mathbf{r} \right\rangle , \label{eq:R201} \end{equation}\]
\[\begin{equation} \psi ( \mathbf{r _ 0} ) = \delta( \mathbf{r} - \mathbf{r _ 0} ) . \label{eq:R202} \end{equation}\]
Interpretação da \(\eqref{eq:R202}\): A função de onda de posição no espaço de posição é a delta de Dirac.
Agora vamos levar a função de onda de posição do espaço de posição para o espaço de momento, substituindo \(\eqref{eq:R202}\) em \(\eqref{eq:R101}\):
\[\begin{equation} \psi ( \mathbf{p} ) = \int d^3r\ e^{-i \mathbf{p} \cdot \mathbf{r} } \delta( \mathbf{r} - \mathbf{r _ 0} ) . \label{eq:R203} \end{equation}\]
A integral pode ser facilmente resolvida pela técnica da filtragem-delta: o resultado é a função multiplicativa no ponto \( \mathbf{r _ 0} \):
\[\begin{equation} \psi ( \mathbf{p} ) = e^{-i \mathbf{p} \cdot \mathbf{r _ 0} } . \label{eq:R204} \end{equation}\]
Interpretação da \(\eqref{eq:R204}\): A função de onda de posição no espaço de momento é uma onda plana.
Conclusão: Uma partícula no estado \(\eqref{eq:R200}\) possui posição certa, a posição \( \mathbf{r} = \mathbf{r_0} \), todavia, seu momento é totalmente incerto, pois \(\eqref{eq:R204}\) gera \(|\psi ( \mathbf{p} )|^2={\rm constante}\), para qualquer valor de \( \mathbf{p} \).
\({ }\)
\(2^{\rm o}\) EXEMPLO:
Considere o vetor \(\left| \Upsilon \right\rangle\) em certo estado de autovetor do operador de momento:
\[\begin{equation} \left| \Upsilon \right\rangle = \left| \mathbf{p _ 0} \right\rangle . \label{eq:R200p} \end{equation}\]
Agora considere esta matemática sobre \(\eqref{eq:R200p}\):
\[\begin{equation} \left\langle \mathbf{p _ 0} \middle| \Upsilon \right\rangle = \left\langle \mathbf{p _ 0} \middle| \mathbf{p} \right\rangle , \label{eq:R201p} \end{equation}\]
\[\begin{equation} \Upsilon ( \mathbf{p _ 0} ) = \delta( \mathbf{p} - \mathbf{p _ 0} ) . \label{eq:R202p} \end{equation}\]
Interpretação da \(\eqref{eq:R202p}\): A função de onda de momento no espaço de momento é a delta de Dirac.
Agora vamos levar a função de onda de momento do espaço de momento para o espaço de posição, substituindo \(\eqref{eq:R202p}\) em \(\eqref{eq:R100}\):
\[\begin{equation} \Upsilon ( \mathbf{r} ) = \int d^3p\ e^{i \mathbf{p} \cdot \mathbf{r} } \delta( \mathbf{p} - \mathbf{p _ 0} ) . \label{eq:R203p} \end{equation}\]
Novamente a integral pode ser facilmente resolvida pela técnica da filtragem-delta: o resultado é a função multiplicativa no ponto \( \mathbf{p _ 0} \):
\[\begin{equation} \Upsilon ( \mathbf{r} ) = e^{i \mathbf{p _ 0} \cdot \mathbf{r} } . \label{eq:R204p} \end{equation}\]
Interpretação da \(\eqref{eq:R204p}\): A função de onda de momento no espaço de posição é uma onda plana.
Conclusão: Uma partícula no estado \(\eqref{eq:R200p}\) possui momento certo, o momento \( \mathbf{p} = \mathbf{p_0} \), todavia, sua posição é totalmente incerta, pois \(\eqref{eq:R204p}\) gera \(|\Upsilon ( \mathbf{r} )|^2={\rm constante}\), para qualquer valor de \( \mathbf{r} \).
6 Desafio
Agora que aprendemos trabalhar com as Representações de Vetores no Espaço de Hilbert, podemos avançar na aplicação dos conceitos.
Um problema extremamente importante em mecânica quântica é resolver a equação de Schrödinger.
A equação de Schrödinger é a equação de autovalor de energia expressa na base de posição. Tente provar que:
\[\begin{equation} \hat{H} \left| \Psi _ {\scriptsize E} \right\rangle = E \left| \Psi _ {\scriptsize E} \right\rangle , \label{eq:R300} \end{equation}\]
se transforma em:
\[\begin{equation} -\frac{\hbar^2}{2m} \nabla ^2 \Psi _ {\scriptsize E} ( \mathbf{r} ) + V( \mathbf{r} ) \Psi _ {\scriptsize E} ( \mathbf{r} ) = E\, \Psi _ {\scriptsize E} ( \mathbf{r} ) . \label{eq:R301} \end{equation}\]
O lado direito de \(\eqref{eq:R300}\) é imediato: \(\left\langle \mathbf{r} \middle| \Psi _ {\scriptsize E} \right\rangle\) é a função de onda de energia no espaço de posição:
\[\begin{equation} \left\langle \mathbf{r} \middle| \Psi _ {\scriptsize E} \right\rangle = \Psi _ {\scriptsize E} ( \mathbf{r} ) . \label{eq:R302} \end{equation}\]
O desafio está em resolver o lado esquerdo de \(\eqref{eq:R300}\): \(\left\langle \mathbf{r} \middle| \hat{H} \middle| \Psi _ {\scriptsize E} \right\rangle\). A solução está no livro (Zettili 2009).