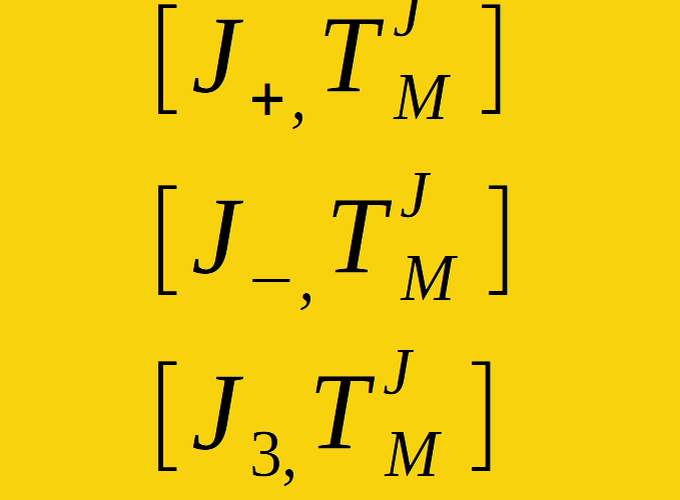1 Introdução
Certo dia nosso professor nos ensinou o que é o ESCALAR: Um “objeto” que tem as propriedades dos números reais. Passados alguns anos, outro professor nos falou sobre o VETOR: Um “objeto” que se caracteriza pelas propriedades de módulo, direção e sentido. Prosseguindo nos estudos, mais um professor nos mostrou o OPERADOR VETORIAL: Um “objeto” caracterizado pelas propriedades de uma tríade de operadores. Em um dia notável, o professor Giulio Racah nos apresentou o OPERADOR TENSORIAL IRREDUTÍVEL: Um “objeto” que se caracteriza pelas… Falaremos mais à frente sobre o assunto, mas podemos ver sua definição em: Racah, G., Theory of Complex Spectra. I, Physical Review, 61, p.186 (1942) (Racah 1942a); Racah, G., Theory of Complex Spectra. II, Physical Review, 62, p.438 (1942) (Racah 1942b).
Este artigo tem como objetivo apresentar a definição de Racah para o operador tensorial irredutível e demonstrar que o operador vetorial do momento angular (escrito pelas componentes esféricas) é um operador tensorial irredutível de grau 1.
2 A notação adotada
A notação utilizada é a mesma do livro (L C Biedenharn 1984).
As componentes cartezianas do momento angular (Jx,Jy,Jz) são escritas como (J1,J2,J3), quer dizer, escreve-se o momento angular como:
J=J1ˆe1+J2ˆe2+J3ˆe3.
As componentes esféricas do momento angular (J+1,J0,J−1) são escritas em função das componentes cartezianas:
J+1=−1√2(J1+iJ2),J0=J3,J−1=1√2(J1−iJ2).
Os operadores escada (J+,J−) são escritos em função dos operadores (J1,J2):
J+=J1+iJ2,J−=J1−iJ2.
Nota 1: Na língua inglesa, os operadores (3) são chamados de ladder operators (operadores escada); também são conhecidos como raising and lowering operators (operadores de elevação e de abaixamento).
Nota 2: Inspecionando (2) e (3), escreve-se as componentes esféricas em termos dos operadores escadas:
J+1=−1√2J+,J0=J3,J−1=1√2J−.
3 A definição de Racah
Racah definiu que um “objeto” é um operador tensorial irredutível quando as componentes desse “objeto” satisfazem as regras (Racah 1942b):
[J+, TJM]=√(J−M)(J+M+1) TJM+1,[J−, TJM]=√(J+M)(J−M+1) TJM−1,[J3, TJM]=M TJM.
Em (5), TJM são as componentes do operador tensorial irredutível TJ. O grau, ou a ordem de TJ é J. Sendo M=J,J−1,…,−J, o operador tensorial é formado por (2J+1) componentes: TJJ, TJJ−1, …, TJ−J. De fato, um operador tensorial irredutível de grau J é um conjunto de (2J+1) operadores TJM.
4 Operador vetorial como operador tensorial
Vamos demonstrar que o operador vetorial do momento angular (escrito pelas componentes esféricas) é um operador tensorial irredutível de grau 1. Para isso, vamos resolver — simultaneamente — os lados esquerdo e direito de (5) e verificar se há igualdade.
Nota 1: As relações de comutação das componentes Cartesianas do operador do momento angular são:
[J1,J2]=iJ3
[J3,J1]=iJ2
[J2,J3]=iJ1
Nota 2: O símbolo ◼ significa DEMONSTRADO.
Resolução para J+:
[J+, J0]=√(1−0)(1+0+1) J10+1[(J1+iJ2), J3]=√2 J1+1[J1, J3]+i[J2, J3]=−iJ2+i(iJ1)=−(J1+iJ2)=√2 J+1=◼
Resolução para J−:
[J−, J0]=√(1+0)(1−0+1) J10−1[(J1−iJ2), J3]=√2 J1−1[J1, J3]−i[J2, J3]=−iJ2−i(iJ1)=(J1−iJ2)=√2 J−1=◼
Resolução para J3:
[J3, J0]=0⋅J10[J3, J3]=0=◼
5 Conclusão
Por obedecerem as regras de Racah (5), as componentes esféricas do operador vetorial do momento angular J (J+1,J0,J−1) são as componentes do operador tensorial irredutível J1 (J1+1,J10,J1−1).