1 Introdução

Há duas maneiras de se discutir o momento angular orbital na mecânica quântica (Thompson 1994). Uma, usa a definição do momento angular clássico, a saber, o produto vetorial da posição da partícula pelo seu momento linear, logo, em seguida, faz-se a conversão dos elementos clássicos pelos operadores quânticos (posição e momento linear) — disso resulta no operador do momento angular orbital. A outra, utiliza as propriedades geométricas das rotações e, assim, deduz-se diretamente o operador do momento angular orbital, sem a necessidade de se lançar mão da definição clássica.

O objetivo deste artigo é deduzir o operador do momento angular orbital partindo da definição clássica do momento angular. Ademais, apresentar suas autofunções, seus autovalores e sua representação matrial.

2 O momento angular orbital

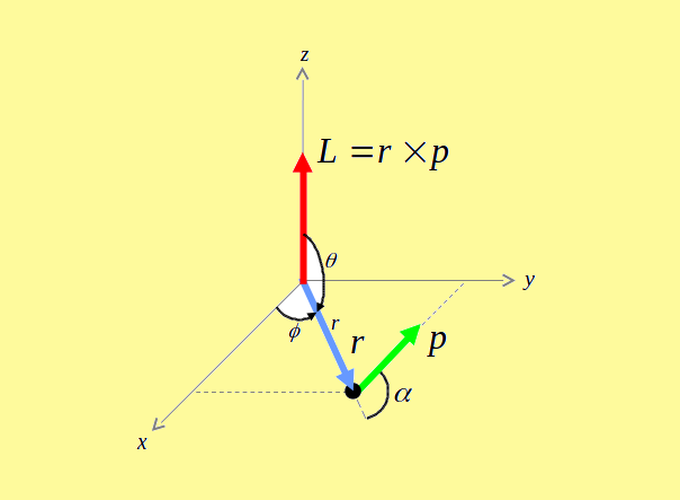
O momento angular orbital é representado por \(\boldsymbol{L}\). Ele é definido pelo produto vetorial \(\boldsymbol{L} = \boldsymbol{r} \times \boldsymbol{p}\) (Herbert Goldstein 2001). Conforme se vê na Figura 2.1, o momento angular orbital se relaciona com o ângulo \(\alpha\) entre a posição \(\boldsymbol{r}\) e o momento linear \(\boldsymbol{p}\). Seu módulo é: \(|\boldsymbol{L}| = r \hspace{1pt} p \hspace{2pt}\mathrm{sen}\alpha\), e sua direção é perpendicular ao plano que contém os vetores \(\boldsymbol{r}\) e \(\boldsymbol{p}\). Já seu sentido é determinado pela regra da mão direita, fazendo \(\boldsymbol{r}\) correr em direção à \(\boldsymbol{p}\).

A natureza radial e angular do momento angular orbital favorece um sistema de coordenadas não-cartesiano, como o sistema esférico, de coordenadas radial \(r\), polar \(\theta\) e azimutal \(\phi\), sendo as faixas de valores: \(0 \leqslant r < \infty\), \(0 \leqslant \theta \leqslant \pi\), \(0 \leqslant \phi \leqslant 2\pi\).

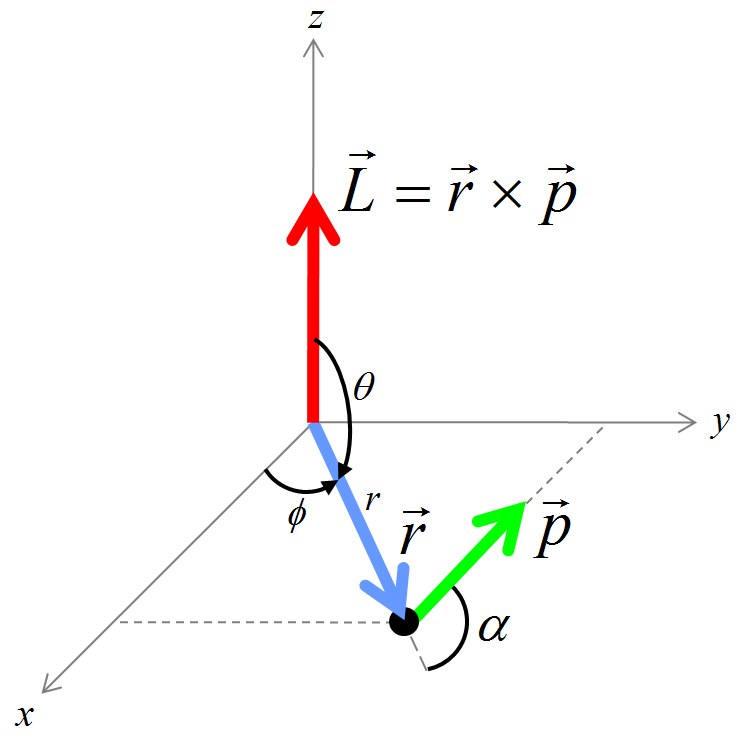
Figura 2.1: O momento angular orbital clássico.

A Figura 2.1 mostra que o momento angular orbital clássico é o vetor \(\boldsymbol{L} = (L_x , L_y , L_z)\). Na mecânica quântica, o momento angular orbital continua sendo um vetor, no sentido de possuir 3 componentes, todavia, o tratamento quântico utiliza operadores nos lugares dos elementos clássicos (Liboff 2002). O vetor, então, é um vetor de operadores representado por \(\hat{\boldsymbol{L}} = (\hat{L}_x , \hat{L}_y , \hat{L}_z)\).

No sistema cartesiano, as componentes do momento angular orbital clássico podem ser determinadas pelo determinante:

\[ \boldsymbol{L} = \begin{vmatrix} \hat{e} _ x & \hat{e} _ y & \hat{e} _ z \\ x & y & z \\ p _ x & p _ y & p _ z \end{vmatrix}. \tag{2.1} \]

O que resulta em:

\[ \begin{aligned} L _ x &= yp _ z - zp _ y; \\ L _ y &= zp _ x - xp _ z; \\ L _ z &= xp _ y - yp _ x. \end{aligned} \tag{2.2} \]

Na mecânica quântica, o operador do momento angular orbital deriva diretamente da estrutura do \(\boldsymbol{L}\), fazendo a conversão dos elementos clássicos em operadores:

\[ \begin{aligned} x &\to \hat{x} = x; \\ y &\to \hat{y} = y; \\ z &\to \hat{z} = z; \\ p _ x &\to \hat{p} _ x = -\imath \hbar \frac{\partial}{\partial x}; \\ p _ y &\to \hat{p} _ y = -\imath \hbar \frac{\partial}{\partial y}; \\ p _ z &\to \hat{p} _ z = -\imath \hbar \frac{\partial}{\partial z}. \end{aligned} \tag{2.3} \]

Substituindo (2.2) em (2.3), as componentes do operador \(\hat{\boldsymbol{L}}\) se escrevem:

\[ \begin{aligned} \hat{L} _ x &= \hat{y}\hat{p} _ z - \hat{z}\hat{p} _ y = -\imath \hbar \left(y\frac{\partial}{\partial z} - z\frac{\partial}{\partial y} \right); \\ \hat{L} _ y &= \hat{z}\hat{p} _ x - \hat{x}\hat{p} _ z = -\imath \hbar \left(z\frac{\partial}{\partial x} - x\frac{\partial}{\partial z} \right); \\ \hat{L} _ z &= \hat{x}\hat{p} _ y - \hat{y}\hat{p} _ x = -\imath \hbar \left(x\frac{\partial}{\partial y} - y\frac{\partial}{\partial x} \right). \end{aligned} \tag{2.4} \]

Em (2.4) temos as componentes cartezianas do \(\hat{\boldsymbol{L}}\) escritas em função das coordenadas cartezianas. Agora, em função das coordenadas esféricas, as componentes cartezianas do \(\hat{\boldsymbol{L}}\) se escrevem:

\[ \begin{aligned} \hat{L} _ x &= \imath \hbar \left(\hspace{2pt}\mathrm{sen}\phi \frac{\partial}{\partial \theta} + \hspace{2pt}\mathrm{cotg}\theta \hspace{2pt}\mathrm{cos}\phi \frac{\partial}{\partial \phi} \right) ; \\ \hat{L} _ y &= \imath \hbar \left(- \hspace{2pt}\mathrm{cos}\phi \frac{\partial}{\partial \theta} + \hspace{2pt}\mathrm{cotg}\theta \hspace{2pt}\mathrm{sen}\phi \frac{\partial}{\partial \phi} \right) ; \\ \hat{L} _ z &= -\imath \hbar \frac{\partial}{\partial \phi} . \end{aligned} \tag{2.5} \]

Como vimos, o operador do \(\boldsymbol{L} = (L_x , L_y , L_z)\) é o operador \(\hat{\boldsymbol{L}} = (\hat{L}_x , \hat{L}_y , \hat{L}_z)\), de componentes cartezianas (2.4) ou (2.5): Escrito na forma (2.5), não se atua na coordenada radial \(r\), somente nas coordenadas angulares \(\theta\) e \(\phi\).

O operador do momento angular orbital, ao quadrado, se escreve:

\[ \hat{ \boldsymbol{L} } ^2 = \hat{\boldsymbol{L}} \cdot \hat{\boldsymbol{L}} = \hat{ {L} } _ x ^2 + \hat{ {L} } _ y ^2 + \hat{ {L} } _ z ^2 . \tag{2.6} \]

Em função das coordenadas esféricas, a equação (2.6) tem a forma:

\[ \hat{ \boldsymbol{L} } ^2 = -\hbar ^2 \left( \frac{\partial ^2}{\partial \theta ^2} + \hspace{2pt}\mathrm{cotg}\theta \frac{\partial}{\partial \theta} + \frac{1}{\hspace{2pt}\mathrm{sen}^2 \theta} \frac{\partial ^2}{\partial \phi ^2} \right) . \tag{2.7} \]

3 Autofunções e autovalores do momento angular orbital

A caracterização do momento angular clássico pode ser feita apontando os valores de suas 3 componentes, \(L_x\), \(L_y\) e \(L_z\) (simultâneamente), o que leva a conhecer o valor do módulo ou magnitude \(L\).

O tratamento quântico não caracteriza o momento angular por discriminar os valores das 3 componentes. Conforme esclarece (Liboff 2002), simultâneamente, determina-se os valores do módulo e de apenas 1 componente do momento angular — geralmente, prefere-se especificar a componente \(z\).

Vamos explicitar os valores de \(L^2\) e \(L_z\) através das equações de autovalor dos operadores \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L} _ z\). As formas (2.5) e (2.7) não dependem da coordenada radial, por isso, as equações de autovalor geram autofunções que dependem somente das coordenadas angulares:

\[ \begin{aligned} \hat{ \boldsymbol{L} } ^2 \, Y _ {l,m} &= L ^2 \, Y _ {l,m}; \\ \hat{L} _ z \, Y _ {l,m} &= L _ z \, Y _ {l,m}. \end{aligned} \tag{3.1} \]

Os autovalores \(L^2\) e \(L_z\) possuem os seguintes valores:

\[ \begin{aligned} L ^2 &= l(l+1) \hbar ^2 ; \\ L _ z &= m \hbar . \end{aligned} \tag{3.2} \]

Apesar de \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L} _ z\) compartilharem as autofunções, os autovalores são bem diferentes: ver as equações (3.1) e (3.2).

As autofunções \(Y_{l,m}(\theta,\phi)\) são conhecidas como harmônicos esféricos. O número \(l\) é o número quântico orbital e o número \(m\) é o número quântico azimutal, ou número quântico magnético. Os valores do número quântico orbital são: \(l=0, 1, 2, 3, \cdots\). Para cada \(l\), os valores do número quântico azimutal são: \(m=l, (l-1), (l-2), \cdots, -l\). A Figura 3.1 torna explícito os harmônicos esféricos para \(l = 0, 1, 2, 3\).

Figura 3.1: Alguns harmônicos esféricos.

Dada uma partícula com momento angular orbital de magnitude \(L = \sqrt{l(l+1)} \hbar\) e componente \(z\), \(L_z = m\hbar\), a densidade de probabilidade da posição \((\theta , \phi)\) é determinada pela relação:

\[ \left| Y_{l,m} \right|^2 = Y_{l,m}^{\ast} (\theta , \phi) \, Y_{l,m} (\theta , \phi) , \tag{3.3} \]

e a probabilidade de essa partícula estar entre \((\theta _1,\theta _ 2)\) e \((\phi _1,\phi _2)\) é determinada pela integral:

\[ {\rm P} _ {l,m} = \int\limits_ {\theta _ 1}^{\theta _ 2} \, \int\limits_ {\phi _ 1}^{\phi _ 2} \left| Y_{l,m} \right|^2 \ {\rm d} \Omega . \tag{3.4} \]

Os harmônicos esféricos são funções normalizadas e ortogonais, pois:

\[ \begin{aligned} \int\limits_ {\theta=0}^{\pi} \, \int\limits_ {\phi=0}^{2\pi} \left| Y_{l,m} \right|^2 \ {\rm d}\Omega &= 1, \ \ {\rm se} \ \bar{l}=l \ {\rm e} \ \overline{m}=m ;\\ &= 0, \ \ {\rm caso\ contr\acute{a}rio} . \end{aligned} \tag{3.5} \]

Nota: \({\rm d}\Omega = \hspace{2pt}\mathrm{sen}\theta \, {\rm d}\theta \, {\rm d}\phi\).

Observando a Figura 3.1, conclui-se que a densidade de probabilidade não depende do ângulo \(\phi\). Por causa disso, pode-se fazer a representação gráfica da densidade de probabilidade anexando o valor de \(\left| Y_{l,m} \right|^2\) a um raio \(R(\theta)\). Daí, fazendo a varredura angular de \(\theta\), o raio \(R(\theta)\) “desenha” pelo espaço, a densidade de probabilidade na forma de uma curva esfericamente simétrica. As Figuras 3.2, 3.3 e 3.4 apresentam as curvas das densidades de probabilidade geradas por esse método.

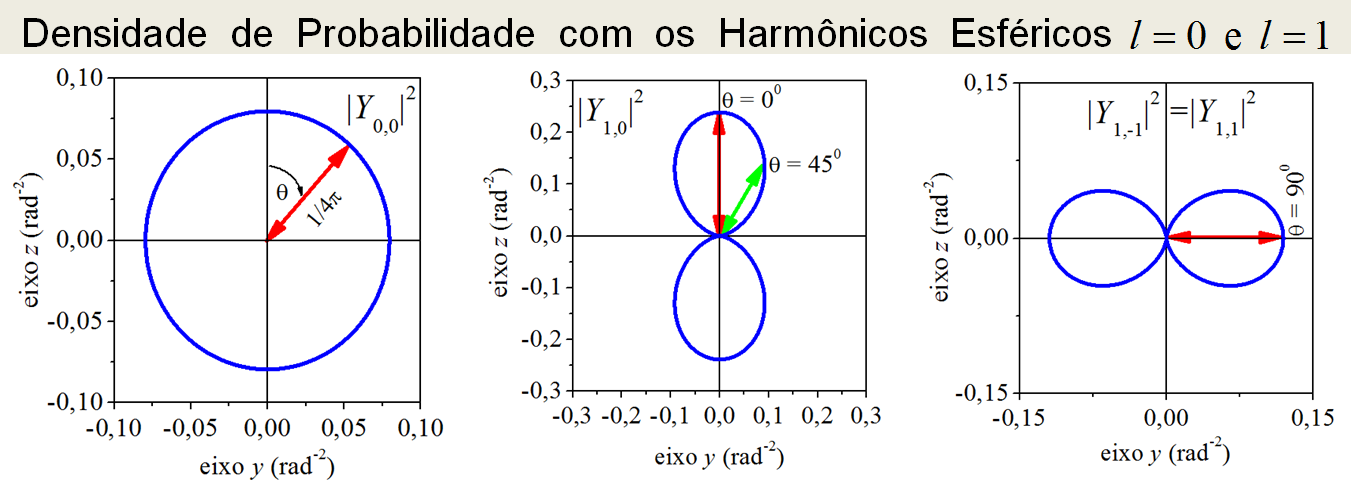
Figura 3.2: Densidade de probabilidade para l = 0 e l = 1.

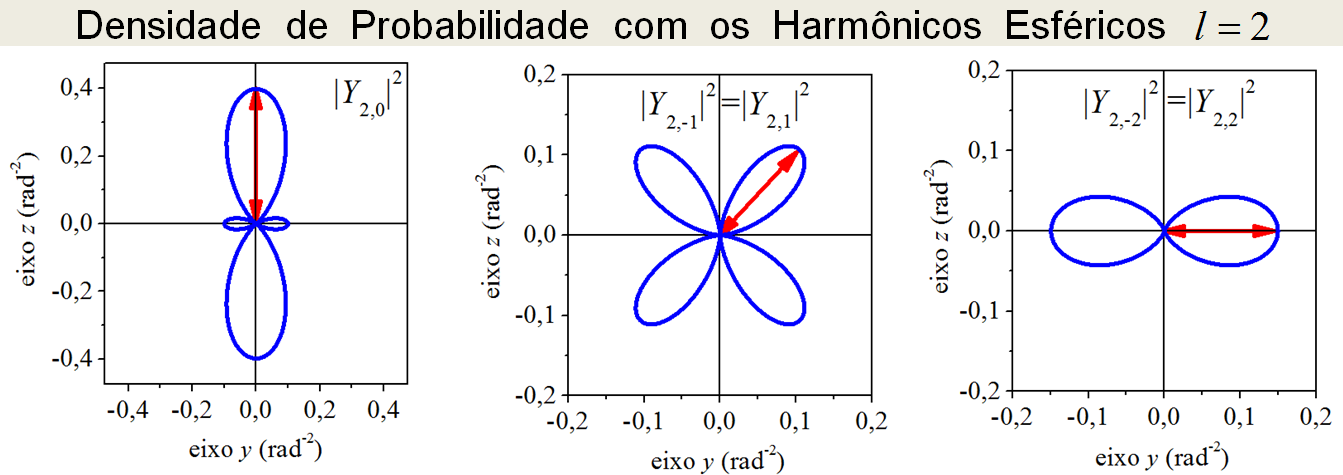
Figura 3.3: Densidade de probabilidade para l = 2.

Figura 3.4: Densidade de probabilidade para l = 3.

Como foram construídos, os contornos das curvas indicam a magnitude da densidade de probabilidade na direção do ângulo polar \(\theta\), sendo que esse ângulo parte do eixo \(z\). Para auxiliar a visualização, setas, indicando a magnitude da densidade, foram desenhadas em certas direções angulares. Visto que a densidade de probabilidade não depende do ângulo azimutal \(\phi\), as figuras devem ser rodadas sobre o eixo \(z\) para se visualizar as figuras das densidades tridimensionais. Como se vê, exceto para \(l=0\), que gera uma densidade constante, as demais densidades de probabilidade apresentam preferências angulares. Por exemplo, observando a Figura 3.2, a maior probabilidade de encontrar a partícula no estado \(Y_{1,0}\) é em \(\theta = 0^0\), todavia, se a partícula estiver no estado \(Y_{1,1}\), a maior probabilidade de encontrá-la será em \(\theta = 90^0\), pois, em \(\theta = 0^0\), a probabilidade é zero.

4 Operadores compatíveis e incompatíveis

Neste capítulo, vamos analisar situações em que se manifesta momento angular orbital, nosso objetivo, é entender quando dois operadores são compatíveis e quando são incompatíveis.

Considere uma partícula orbitando livre em torno de um ponto central, como se estivesse sobre a superfície de uma esfera, executando “voltas e mais voltas.” À rotação associa-se um momento angular orbital. Nós, então, montamos uma experiência para medir a magnitude do momento angular. Vamos supor que encontramos \(L=\sqrt{12}\hbar\), correspondente ao número quântico orbital \(l=3\). Logo em seguida, montamos outra experiência para medir a componente \(z\) do momento angular orbital de magnitude \(\sqrt{12}\hbar\). Quais seriam os possíveis resultados da nova experiência? A previsão quântica diz que poderíamos encontrar qualquer um dos seguintes valores:

\[ \begin{aligned} L _ {z} &= \hspace{8pt} 3\hbar, \\ {\rm ou} &= \hspace{8pt} 2\hbar, \\ {\rm ou} &= \hspace{8pt} 1\hbar, \\ {\rm ou} &= \hspace{8pt} 0\hbar, \\ {\rm ou} &= -1\hbar, \\ {\rm ou} &= -2\hbar, \\ {\rm ou} &= -3\hbar. \end{aligned} \tag{4.1} \]

Os possíveis resultados (4.1) podem ser geometricamente representados por vetores de comprimento proporcional à \(\sqrt{12}\hbar\), orientados de tal maneira que suas projeções no eixo \(z\) sejam proporcionais aos valores de \(L_z\), conforme aparece na Figura 4.1.

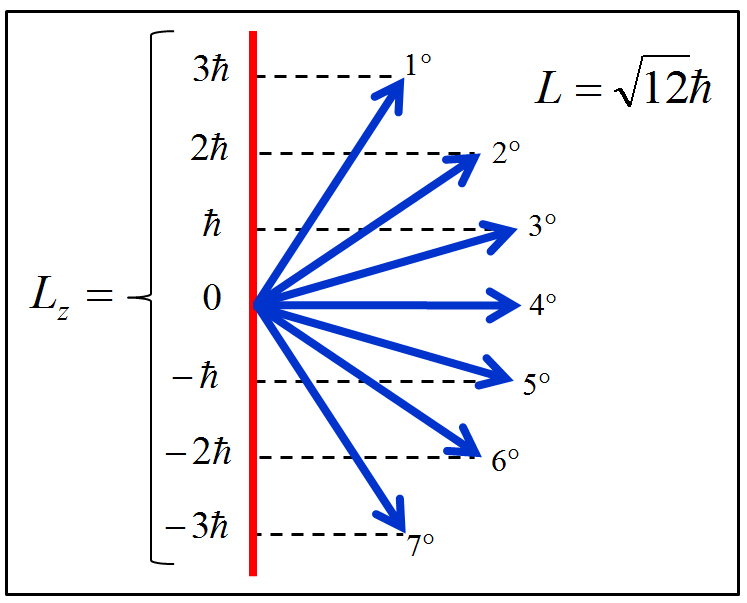
Figura 4.1: Ilustração dos momentos angulares orbitais (4.1) .

Após a primeira medição, discernimos qual a magnitude do momento angular, mas ainda não sabemos sua direção, pois há 7 possibilidades — ver novamente a Figura 4.1. Diz-se que \(L=\sqrt{12}\hbar\) é 7 vezes degenerado, e conclui-se que está associado a uma superposição de 7 autoestados: \(Y_{3,3},Y_{3,2},Y_{3,1},Y_{3,0},Y_{3,-1},Y_{3,-2},Y_{3,-3}\).

Vamos, então, supor que uma segunda medição resulte em \(L_z=2\hbar\), equivalente ao número quântico azimutal \(m=2\). Agora podemos discernir qual é a direção do momento angular orbital, pois somos induzidos a perceber de que se trata do segundo momento da Figura 4.1.

Concluímos, após os dois experimentos mentais, que a partícula estaria no estado \(Y_{3,2}\), autoestado comum de \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L}_z\). Concluímos, também, que a \(1^\underline{a}\) experiência, relacionada com \( \hat{ \boldsymbol{L} } ^2 \), somente revela o valor do módulo do momento angular orbital, e que a \(2^\underline{a}\) experiência, relacionada com \(\hat{L}_z\), completa a caracterização desse momento, ajudando a distinguir qual é a sua orientação.

\(\blacklozenge\ \) E se mudássemos a ordem das experiências?

A Figura 4.2 ilustra a nova sequência: \(1^\underline{a}\) experiência relacionada com \(\hat{L}_z\), \(2^\underline{a}\) experiência relacionada com \( \hat{ \boldsymbol{L} } ^2 \).

Ao fazer a medição da componente \(z\) do momento angular orbital, iríamos encontrar \(L_z=2\hbar\). Daí, perguntaríamos: Qual é o valor do módulo? A resposta estaria condicionada aos valores que satisfizessem a expressão \(L = \sqrt{l(l+1)} \hbar\):

\[ \begin{aligned} L &= 0, \\ {\rm ou} &= \sqrt{2} \hbar, \\ {\rm ou} &= \sqrt{6} \hbar, \\ {\rm ou} &= \sqrt{12} \hbar, \\ {\rm ou} &= \sqrt{20} \hbar, \\ &\ \, \vdots \end{aligned} \tag{4.2} \]

Em seguida, faríamos a medição do módulo, por exemplo, com resultado \(L=\sqrt{12}\hbar\). Por fim, saberíamos que a partícula se encontra no estado \(Y_{3,2}\), representado pelo terceiro vetor da Figura 4.2.

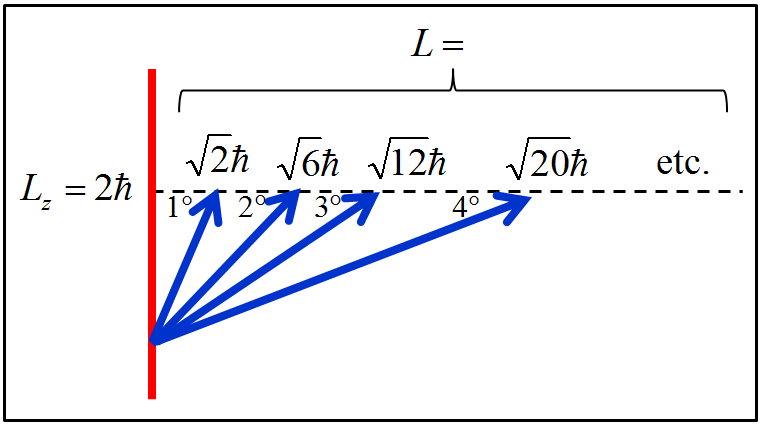
Figura 4.2: Ilustração dos momentos angulares orbitais (4.2).

As experiências que acabamos de considerar, nos ajudam a entender que os operadores \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L}_z\) possibilitam a montagem de experiências compatíveis (que podem coexistir), sendo o registro da experiência \( \hat{ \boldsymbol{L} } ^2 \) complementar ao registro da experiência \(\hat{L}_z\), e vice-versa. Dizemos, então, que os operadores \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L}_z\) são operadores compatíveis.

Todavia, há situações em que as experiências são incompatíveis. Por exemplo, se montássemos experiências realcionadas com \(\hat{L}_z\) e \(\hat{L}_x\), chegaríamos à conclusão que a experiência \(\hat{L}_x\) não completaria a informação da experiência \(\hat{L}_z\). Isso porque o autoestado de \(\hat{L}_x\) não é solução da equação de autoestado de \(\hat{L}_z\). Nesse caso, dizemos que os operadores \(\hat{L}_z\) e \(\hat{L}_x\) são operadores incompatíveis.

Experiências compatíveis só ocorrem quando os operadores compartilham o mesmo conjunto de autoestados, como o par \( \hat{ \boldsymbol{L} } ^2 \) e \(\hat{L}_z\), que usa o conjunto \(Y_{l,m}\) em comum. E, para saber se dois operadores, por exemplo, \(\hat{A}\) e \(\hat{B}\), são operadores compatíveis e têm autofunções em comum, usa-se uma ferramenta matemática chamada comutador:

\[ \left[ \hat{A} , \hat{B} \right] = \hat{A}\hat{B} - \hat{B}\hat{A} . \tag{4.3} \]

Daí, diz-se que \(\hat{A}\) e \(\hat{B}\) são operadores compatíveis e possuem autofunções em comum, se \(\hat{A}\) e \(\hat{B}\) comutam entre si, ou seja, se:

\[ \hat{A}\hat{B} = \hat{B}\hat{A} \ \implies \ \left[ \hat{A} , \hat{B} \right] = 0 . \tag{4.4} \]

O teste do comutador mostra que as componentes do operador do momento angular não comutam entre si:

\[ \begin{aligned} \left[ \hat{L} _ x , \hat{L} _ y \right] &= \imath \hbar\hat{L} _ z; \\ \left[ \hat{L} _ y , \hat{L} _ z \right] &= \imath \hbar\hat{L} _ x; \\ \left[ \hat{L} _ z , \hat{L} _ x \right] &= \imath \hbar\hat{L} _ y. \end{aligned} \tag{4.5} \]

Por outro lado, \( \hat{ \boldsymbol{L} } ^2 \) comuta com todas componentes do \(\hat{\boldsymbol{L}}\):

\[ \begin{aligned} \left[ \hat{ \boldsymbol{L} } ^2 , \hat{L} _ x \right] &= 0; \\ \left[ \hat{ \boldsymbol{L} } ^2 , \hat{L} _ y \right] &= 0; \\ \left[ \hat{ \boldsymbol{L} } ^2 , \hat{L} _ z \right] &= 0. \end{aligned} \tag{4.6} \]

Usando o critério (4.4) , pode-se afirmar que os operadores (4.5) são incompatíveis (não compartilham suas autofunções), já os operadores (4.6) são compatíveis e, por isso, compartilham suas autofunções: Segundo (3.1) , compartilham as autofunções harmônicos esféricos — ver a Figura 3.1.

Uma visão extendida de operações e propriedades de comutadores pode ser vista na Figura 4.3.

Figura 4.3: Operações e propriedades de comutadores.

5 O princípio de incerteza generalizado

O princípio de incerteza é de autoria de W. Heisenberg (Heisenberg 1927). Uma formulação geral e aplicada em particular ao caso do momento angular foi publicada por H.P. Robertson (Robertson 1929). A formulação generalizada se aplica a qualquer par de operadores \(\hat{A}\) e \(\hat{B}\), que possuem autovalores \(A\) e \(B\):

\[ \Delta A \, \Delta B \, \geqslant \, \frac{1}{2} \, \left| \left< \imath \left[ \hat{A} , \hat{B} \right] \, \right> \, \right| . \tag{5.1} \]

A sequência matemática em (5.1) é: \((1^\underline{o})\) fazer o comutador \(\left[ \cdots \right]\), \((2^\underline{o})\) fazer o valor esperado \(\left< \cdots \right>\), e \((3^\underline{o})\) fazer o módulo \(\left| \cdots \right|\).

Vamos, então, desenvolver o princípio de incerteza generalizado utilizando os operadores \(\hat{L}_x\) e \(\hat{L}_y\), de autovalores \(L_x\) e \(L_y\), respectivamente:

\[ \Delta L _ x \, \Delta L _ y \, \geqslant \, \frac{1}{2} \left| \left< \imath \left[ \hat{L} _ x , \hat{L} _ y \right] \right> \right| . \tag{5.2} \]

Segundo (4.5), o \((1^\underline{o})\) passo resulta em:

\[ \imath \left[ \hat{L} _ x , \hat{L} _ y \right] = - \hbar\hat{L} _ z . \tag{5.3} \]

O \((2^\underline{o})\) passo resulta em:

\[ \left< \imath \left[ \hat{L} _ x , \hat{L} _ y \right] \right> = -\hbar \left< \hat{L} _ z \right> . \tag{5.4} \]

E o \((3^\underline{o})\) passo resulta em:

\[ \left| \left< \imath \left[ \hat{L} _ x , \hat{L} _ y \right] \right> \right| = \hbar \left| \left< \hat{L} _ z \right> \right| . \tag{5.5} \]

Levando o resultado (5.5) ao princípio (5.1), tem-se:

\[ \Delta L _ x \, \Delta L _ y \, \geqslant \, \frac{1}{2} \hbar \left| \left< \hat{L} _ z \right> \right| . \tag{5.6} \]

A relação (5.6) exige que se determine o valor esperado do operador \(\hat{L}_z\). Para isso, vamos supor uma partícula no autoestado \(Y_{3,2}\), de número azimutal \(m=2\). Por meio de (3.1): \(\hat{L}_z \, Y_{3,2} = 2\hbar \,Y_{3,2}\). Ademais, usando o fato dos harmônicos esféricos serem funções normalizadas e ortogonais (3.5):

\[ \begin{aligned} \left< \hat{L} _ z \right> &= \int\limits_ {\theta=0}^{\pi} \, \int\limits_ {\phi=0}^{2\pi} Y _ {3,2} ^{\ast} \, \hat{L} _ z \, Y _ {3,2} \ {\rm d}\Omega \\ &= 2\hbar \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {3,2} ^{\ast} \, Y _ {3,2} \ {\rm d}\Omega \\ &= 2\hbar. \end{aligned} \tag{5.7} \]

Portanto, substituindo (5.7) em (5.6):

\[ \Delta L _ x \, \Delta L _ y \, \geqslant \, \hbar ^2 . \tag{5.8} \]

No geral, supondo a partícula no autoestado \(Y_{l,m}\), tem-se:

\[ \left< \hat{L} _ z \right> = m\hbar ; \tag{5.9} \]

o que implica em:

\[ \Delta L _ x \, \Delta L _ y \, \geqslant \, \frac{1}{2} m \hbar ^2 . \tag{5.10} \]

Como se deve interpretar o resultado (5.10)? A partícula é preparada em \(Y_{l,m}\): autoestado de \(\hat{L}_z\), mas não de \(\hat{L}_x\), nem de \(\hat{L}_y\). Por isso, em uma medição de \(L_x\), qualquer autovalor de \(\hat{L}_x\) poderá fazer parte do registro. Em uma série de medições, o espectro dos resultados fica disperso, com desvio padrão \(\Delta L_x\). Analogamente, em medições de \(L_y\), o espectro dos resultados também é disperso, com desvio padrão \(\Delta L_y\). O resultado (5.10) garante que o produto das dispersões parte de \(\frac{1}{2} m \hbar ^2\), não podendo ser menor.

A respeito dos autovalores dos operadores \(\hat{L}_x\) e \(\hat{L}_y\), entende-se que todas direções no espaço são fisicamente equivalentes, não há motivo para a quantização do eixo \(x\) ou \(y\) ser diferente da quantização do eixo \(z\). Se o autovalor de \(\hat{L}_z\) é o valor \(L_z=m\hbar\), os autovalores de \(\hat{L}_x\) e \(\hat{L}_y\) serão os valores \(L_x=m_x\hbar\) e \(L_y=m_y\hbar\), sendo \(m_x\) e \(m_y\) inteiros dependentes do número quântico orbital: \(m_x=l, (l-1), ..., -l\); e \(m_y=l, (l-1), ..., -l\).

Em nossa mente, estamos trabalhando com uma partícula preparada no estado \(Y_{3,2}\), caracterizada com \(L=\sqrt{12}\hbar\) e, especificamente, possuindo componente \(z\) igual a \(L_z=2\hbar\). Uma experiência, montada para efetuar a medição da componente \(x\) dessa partícula, tem como possíveis resultados os autovalores de \(\hat{L}_x\):

\[ \begin{aligned} L _ {x} &= \hspace{8pt} 3\hbar, \\ {\rm ou} &= \hspace{8pt} 2\hbar, \\ {\rm ou} &= \hspace{8pt} 1\hbar, \\ {\rm ou} &= \hspace{8pt} 0\hbar, \\ {\rm ou} &= -1\hbar, \\ {\rm ou} &= -2\hbar, \\ {\rm ou} &= -3\hbar. \end{aligned} \tag{5.11} \]

Em uma série de medições, de partículas no estado \(Y_{3,2}\), o resultado médio será:

\[ \left< \hat{L} _ x \right> = \frac{3\hbar+2\hbar+1\hbar+0-1\hbar-2\hbar-3\hbar}{7} = 0 . \tag{5.12} \]

Analogamente, se a experiência fosse montada para efetuar a medição da componente \(y\):

\[ \left< \hat{L} _ y \right> = \frac{3\hbar+2\hbar+1\hbar+0-1\hbar-2\hbar-3\hbar}{7} = 0 . \tag{5.13} \]

As médias (5.12) e (5.13) resultam em zero, mas, individualmente, as leituras das medições vão se distribuir em curvas estatísticas, tipo gaussiana, com grau de dispersão \(\Delta L _ x\) e \(\Delta L _ y\) e produto (5.10).

A respeito dos autoestados dos operadores \(\hat{L}_x\) e \(\hat{L}_y\), pode-se representá-los por \(|l,m_x \rangle _x\) e \(|l,m_y \rangle _y\), respectivamente. Então, antes de se iniciar a medição de \(L_x\), o estado \(Y_{3,2}\) está em uma superposição linear de \(|l,m_x \rangle _x\), do tipo:

\[ Y _ {3,2} = {\rm C} _ { 3}^x|3, 3\rangle _ x + {\rm C} _ { 2}^x|3, 2\rangle _ x + {\rm C} _ { 1}^x|3, 1\rangle _ x + {\rm C} _ { 0}^x|3, 0\rangle _ x + {\rm C} _ {-1}^x|3,-1\rangle _ x + {\rm C} _ {-2}^x|3,-2\rangle _ x + {\rm C} _ {-3}^x|3,-3\rangle _ x . \tag{5.14} \]

Em (5.14), \(|{\rm C}_{m_x}^x|^2\) é a probabilidade do estado \(|3,m_x \rangle _x\) ser o estado final da experiência. Usando os coeficientes da superposição, o valor esperado se escreve:

\[ \left< \hat{L} _ x \right> = |{\rm C} _ { 3}^x|^2 ( 3\hbar) + |{\rm C} _ { 2}^x|^2 ( 2\hbar) + |{\rm C} _ { 1}^x|^2 ( 1\hbar) + |{\rm C} _ { 0}^x|^2 ( 0) + |{\rm C} _ {-1}^x|^2 (-1\hbar) + |{\rm C} _ {-2}^x|^2 (-2\hbar) + |{\rm C} _ {-3}^x|^2 (-3\hbar) = 0 . \tag{5.15} \]

Nota: A equação (5.12) é um caso especial da equação (5.15), quando se considera igualdade de probabilidades, ou seja, \(|{\rm C}_{m_x}^x|^2=\frac{1}{7}\).

Analogamente, se a experiência fosse montada para efetuar a medição da componente \(y\) do momento angular orbital, de partículas preparadas no estado \(Y_{3,2}\), teríamos:

\[ Y _ {3,2} = {\rm C} _ { 3}^y|3, 3\rangle _ y + {\rm C} _ { 2}^y|3, 2\rangle _ y + {\rm C} _ { 1}^y|3, 1\rangle _ y + {\rm C} _ { 0}^y|3, 0\rangle _ y + {\rm C} _ {-1}^y|3,-1\rangle _ y + {\rm C} _ {-2}^y|3,-2\rangle _ y + {\rm C} _ {-3}^y|3,-3\rangle _ y . \tag{5.16} \]

E o valor esperado seria:

\[ \left< \hat{L} _ y \right> = |{\rm C} _ { 3}^y|^2 ( 3\hbar) + |{\rm C} _ { 2}^y|^2 ( 2\hbar) + |{\rm C} _ { 1}^y|^2 ( 1\hbar) + |{\rm C} _ { 0}^y|^2 ( 0) + |{\rm C} _ {-1}^y|^2 (-1\hbar) + |{\rm C} _ {-2}^y|^2 (-2\hbar) + |{\rm C} _ {-3}^y|^2 (-3\hbar) = 0 . \tag{5.17} \]

6 O operador de levantamento e de abaixamento

Agora vamos desenvolver ferramentas matemáticas que nos ajudarão a resolver o que está faltando em (6.1):

\[ \begin{aligned} \hat{L} _ x \, Y _ {l,m} &= \, ? \\ \hat{L} _ y \, Y _ {l,m} &= \, ? \\ \hat{L} _ z \, Y _ {l,m} &= m\hbar \, Y _ {l,m}. \end{aligned} \tag{6.1} \]

Respectivamente, o operador de levantamento e o operador de abaixamento são definidos como:

\[ \begin{aligned} \hat{L} _ { + } \, Y _ {l,m} &= C _ { + } \, Y _ {l,m+1} ; \\ \hat{L} _ { - } \, Y _ {l,m} &= C _ { - } \, Y _ {l,m-1} ; \end{aligned} \tag{6.2} \]

onde:

\[ \begin{aligned} C _ { + } &= \hbar \sqrt{ l(l+1) - m(m+1) } ; \\ C _ { - } &= \hbar \sqrt{ l(l+1) - m(m-1) } . \end{aligned} \tag{6.3} \]

Os nomes são apropriados, pois o operador \(\hat{L}_{+}\) levanta o estado \(Y_{l,m}\) para o estado \(Y_{l,m+1}\), enquanto que o operador \(\hat{L}_{-}\) abaixa o estado \(Y_{l,m}\) para o estado \(Y_{l,m-1}\). Por exemplo:

\[ \begin{aligned} &\hat{L} _ { + } \, Y _ {1, 1} \ \ = 0 ; \\ &\hat{L} _ { + } \, Y _ {1, 0} \ \ = \hbar\sqrt{2} \ Y _ {1, 1} ; \\ &\hat{L} _ { + } \, Y _ {1,-1} = \hbar\sqrt{2} \ Y _ {1, 0} . \end{aligned} \tag{6.4} \]

Outro exemplo:

\[ \begin{aligned} &\hat{L} _ { - } \, Y _ {1, 1} \ \ = \hbar\sqrt{2} \ Y _ {1, 0} ; \\ &\hat{L} _ { - } \, Y _ {1, 0} \ \ = \hbar\sqrt{2} \ Y _ {1,-1} ; \\ &\hat{L} _ { - } \, Y _ {1,-1} = 0 . \end{aligned} \tag{6.5} \]

Os operadores \(\hat{L}_{+}\) e \(\hat{L}_{-}\) definem os operadores \(\hat{L}_x\) e \(\hat{L}_y\), da seguinte maneira:

\[ \begin{aligned} \hat{L} _ { x } &= \frac{1}{2} \left( \hat{L} _ { + } + \hat{L} _ { - } \right) ; \\ \hat{L} _ { y } &= \frac{1}{2\imath} \left( \hat{L} _ { + } - \hat{L} _ { - } \right) . \end{aligned} \tag{6.6} \]

Podemos, então, completar (6.1):

\[ \begin{aligned} \hat{L} _ x \, Y _ {l,m} &= \frac{1}{2} \left( C _ { + } \, Y _ {l,m+1} + C _ { - } \, Y _ {l,m-1} \right) ;\\ \hat{L} _ y \, Y _ {l,m} &= \frac{1}{2\imath} \left( C _ { + } \, Y _ {l,m+1} - C _ { - } \, Y _ {l,m-1} \right) ;\\ \hat{L} _ z \, Y _ {l,m} &= m\hbar \, Y _ {l,m}. \end{aligned} \tag{6.7} \]

Buscando a expressão do desvio padrão da componente \(x\) do momento angular orbital, tem-se que determinar:

\[ \Delta L _ x = \sqrt{\left< \hat{L} _ x^2 \right> - \left< \hat{L} _ x \right> ^2} . \tag{6.8} \]

Primeiro passo, determinar o valor esperado da componente \(x\) do operador do momento angular orbital, usando o fato dos harmônicos esféricos serem funções ortogonais (3.5):

\[ \begin{aligned} \left< \hat{L} _ x \right> &= \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \, \hat{L} _ x \, Y _ {l,m} \ {\rm d}\Omega \\ &= \frac{1}{2} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \, \hat{L} _ + \, Y _ {l,m} \ {\rm d}\Omega + \frac{1}{2} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \, \hat{L} _ - \, Y _ {l,m} \ {\rm d}\Omega \\ &= \frac{1}{2} C _ + \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \, Y _ {l,m+1} \ {\rm d}\Omega + \frac{1}{2} C _ - \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \, Y _ {l,m-1} \ {\rm d}\Omega \\ &= 0 . \end{aligned} \tag{6.9} \]

Nota: O resultado geral (6.9) confirma o resultado específico (5.12).

Segundo passo, determinar o quadrado das componentes \(x\) e \(y\) do operador do momento angular orbital:

\[ \begin{aligned} \hat{L} _ x^2 &= \frac{1}{2} \left( \hat{L} _ { + } + \hat{L} _ { - } \right) \frac{1}{2} \left( \hat{L} _ { + } + \hat{L} _ { - } \right) \\ &= \frac{1}{4} \left( \hat{L} _ { + }^2 + \hat{L} _ { + } \hat{L} _ { - } + \hat{L} _ { - } \hat{L} _ { + } + \hat{L} _ { - }^2 \right) . \end{aligned} \tag{6.10} \]

\[ \begin{aligned} \hat{L} _ y^2 &= \frac{1}{2\imath} \left( \hat{L} _ { + } - \hat{L} _ { - } \right) \frac{1}{2} \left( \hat{L} _ { + } - \hat{L} _ { - } \right) \\ &= \frac{1}{4} \left( - \hat{L} _ { + }^2 + \hat{L} _ { + } \hat{L} _ { - } + \hat{L} _ { - } \hat{L} _ { + } - \hat{L} _ { - }^2 \right) . \end{aligned} \tag{6.11} \]

Ao somar (6.10) e (6.11), lembrando que \( \hat{ \boldsymbol{L} } ^2 = \hat{ {L} } _ x ^2 + \hat{ {L} } _ y ^2 + \hat{ {L} } _ z ^2 \), escreve-se:

\[ \hat{ \boldsymbol{L} } ^2 - \hat{L} _ z^2 = \frac{1}{2} \left( \hat{L} _ { + } \hat{L} _ { - } + \hat{L} _ { - } \hat{L} _ { + } \right) . \tag{6.12} \]

Terceiro passo, usando (6.10), determinar o valor esperado do quadrado da componentes \(x\) do operador do momento angular orbital:

\[ \left< \hat{L} _ x ^2 \right> = \frac{1}{4} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{L} _ { + }^2 + \hat{L} _ { + } \hat{L} _ { - } + \hat{L} _ { - } \hat{L} _ { + } + \hat{L} _ { - }^2 \right) Y _ {l,m} \ {\rm d}\Omega . \tag{6.13} \]

\((1^\underline{o})\) termo de (6.13):

\[ \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{L} _ { + }^2 \right) Y _ {l,m} \ {\rm d}\Omega \propto \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} Y _ {l,m+2} \ {\rm d}\Omega = 0 . \tag{6.14} \]

\((4^\underline{o})\) termo de (6.13):

\[ \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{L} _ { - }^2 \right) Y _ {l,m} \ {\rm d}\Omega \propto \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} Y _ {l,m-2} \ {\rm d}\Omega = 0 . \tag{6.15} \]

Substituindo (6.12), (6.14) e (6.15) em (6.13):

\[ \left< \hat{L} _ x ^2 \right> = \frac{1}{2} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{ \boldsymbol{L} } ^2 - \hat{L} _ z^2 \right) Y _ {l,m} \ {\rm d}\Omega . \tag{6.16} \]

\((1^\underline{o})\) termo de (6.16):

\[ \frac{1}{2} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{ \boldsymbol{L} } ^2 \right) Y _ {l,m} \ {\rm d}\Omega = \frac{1}{2} l(l+1)\hbar^2 \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} Y _ {l,m} \ {\rm d}\Omega = \frac{1}{2} l(l+1)\hbar^2 . \tag{6.17} \]

\((2^\underline{o})\) termo de (6.16):

\[ \frac{1}{2} \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} \left( \hat{L} _ z^2 \right) Y _ {l,m} \ {\rm d}\Omega = \frac{1}{2} m^2\hbar^2 \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l,m} ^{\ast} Y _ {l,m} \ {\rm d}\Omega = \frac{1}{2} m^2\hbar^2 . \tag{6.18} \]

Levando (6.17) e (6.18) à expressão (6.16):

\[ \left< \hat{L} _ x ^2 \right> = \frac{1}{2} \left[ l(l+1) - m^2 \right] \hbar^2 . \tag{6.19} \]

Por fim, substituindo (6.9) e (6.19) na definição (6.8), tem-se a expressão do desvio padrão:

\[ \Delta L _ x = \hbar \sqrt{ \frac{1}{2} \left[ l(l+1) - m^2 \right] } . \tag{6.20} \]

Analogamente:

\[ \Delta L _ y = \hbar \sqrt{ \frac{1}{2} \left[ l(l+1) - m^2 \right] } . \tag{6.21} \]

E o produto resultaria em:

\[ \Delta L _ x \Delta L _ y = \frac{\hbar^2}{2} \left[ l(l+1) - m^2 \right] . \tag{6.22} \]

Vamos voltar ao exemplo da partícula no autoestado \(Y_{3,2}\). Substituindo \(l=3\) e \(m=2\) na equação (6.22), encontramos \(\Delta L _ x \Delta L _ x = 4\hbar^2\). Este valor está de acordo com o resultado do princípio de incerteza, o qual prediz um produto maior que \(\hbar^2\): ver a equação (5.8).

7 A representação matricial do momento angular orbital

\(\underline{\rm Revis\tilde{a}o \ 1}\): Os harmônicos esféricos são funções normalizadas e ortogonais:

\[ \begin{aligned} \int\limits_ {\theta=0}^{\pi} \, \int\limits_ {\phi=0}^{2\pi} Y _ {l',m'} ^{\ast} \, Y _ {l,m} \ {\rm d}\Omega &= 1 \hspace{16pt} [ \ {\rm se} \ \ l'=l \ \ {\rm e} \ \ m'=m \ ]\\ &= 0 \hspace{17pt} [ \ {\rm caso\ contr\acute{a}rio} \ ] \end{aligned} \tag{7.1} \]

\(\underline{\rm Revis\tilde{a}o \ 2}\): Os operadores componente \(z\) e quadrado do operador do momento angular orbital são definidos como:

\[ \begin{aligned} \hat{ \boldsymbol{L} } ^2 \, Y _ {l,m} &= l(l+1) \hbar ^2 \, Y _ {l,m} ; \\ \hat{L} _ z \, Y _ {l,m} &= m \hbar \, Y _ {l,m} . \end{aligned} \tag{7.2} \]

\(\underline{\rm Revis\tilde{a}o \ 3}\): Os operadores de levantamento e de abaixamento são definidos como:

\[ \begin{aligned} \hat{L} _ { + } \, Y _ {l,m} &= C _ { + } \, Y _ {l,m+1} ; \\ \hat{L} _ { - } \, Y _ {l,m} &= C _ { - } \, Y _ {l,m-1} ; \end{aligned} \tag{7.3} \]

onde:

\[ \begin{aligned} C _ { + } &= \hbar \sqrt{ l(l+1) - m(m+1) } ; \\ C _ { - } &= \hbar \sqrt{ l(l+1) - m(m-1) } . \end{aligned} \tag{7.4} \]

\(\underline{\rm Revis\tilde{a}o \ 4}\): Os operadores (7.3) são usados na definição dos operadores:

\[ \begin{aligned} \hat{L} _ { x } &= \frac{1}{2} \left( \hat{L} _ { + } + \hat{L} _ { - } \right) ; \\ \hat{L} _ { y } &= \frac{1}{2\imath} \left( \hat{L} _ { + } - \hat{L} _ { - } \right) . \end{aligned} \tag{7.5} \]

Com as revisões em mente, vamos determinar os elementos de matrizes do momento angular orbital, primeiro para o caso geral \(l\), em seguida, para o caso específico \(l=1\).

\(\blacklozenge\ \) COMPONENTES DE MATRIZES

Componentes do operador quadrado do operador do momento angular orbital:

\[ \begin{aligned} \left[\boldsymbol{L} ^2 \right] _ {m',m} &= \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} \left( \hat{ \boldsymbol{L} } ^2 \right) Y _ {l,m} \ {\rm d}\Omega \\ &= l(l+1)\hbar^2 \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} Y _ {l,m} \ {\rm d}\Omega \\ &= l(l+1)\hbar^2 \hspace{16pt} [ \ {\rm se} \ \ l'=l \ \ {\rm e} \ \ m'=m \ ] \\ &= 0 \hspace{52pt} [ \ {\rm caso\ contr\acute{a}rio} \ ] \end{aligned} \tag{7.6} \]

Componentes do operador da componente \(z\) do operador do momento angular orbital:

\[ \begin{aligned} \left[ \hat{L} _ z \right] _ {m',m} &= \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} \left( \hat{L} _ z \right) Y _ {l,m} \ {\rm d}\Omega \\ &= m\hbar \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} Y _ {l,m} \ {\rm d}\Omega \\ &= m\hbar \hspace{16pt} [ \ {\rm se} \ \ l'=l \ \ {\rm e} \ \ m'=m \ ] \\ &= 0 \hspace{25pt} [ \ {\rm caso\ contr\acute{a}rio} \ ] \end{aligned} \tag{7.7} \]

Componentes do operador de levantamento:

\[ \begin{aligned} \left[ \hat{L} _ + \right] _ {m',m} &= \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} \left( \hat{L} _ + \right) Y _ {l,m} \ {\rm d}\Omega \\ &= C _ + \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} Y _ {l,m+1} \ {\rm d}\Omega \\ &= C _ + \hspace{16pt} [ \ {\rm se} \ \ l'=l \ \ {\rm e} \ \ m'=m+1 \ ] \\ &= 0 \hspace{25pt} [ \ {\rm caso\ contr\acute{a}rio} \ ] \end{aligned} \tag{7.8} \]

Componentes do operador de abaixamento:

\[ \begin{aligned} \left[ \hat{L} _ - \right] _ {m',m} &= \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} \left( \hat{L} _ - \right) Y _ {l,m} \ {\rm d}\Omega \\ &= C _ - \int\limits_ {\theta}^{\pi} \, \int\limits_ {\phi}^{2\pi} Y _ {l',m'} ^{\ast} Y _ {l,m-1} \ {\rm d}\Omega \\ &= C _ - \hspace{16pt} [ \ {\rm se} \ \ l'=l \ \ {\rm e} \ \ m'=m-1 \ ] \\ &= 0 \hspace{25pt} [ \ {\rm caso\ contr\acute{a}rio} \ ] \end{aligned} \tag{7.9} \]

\(\blacklozenge\ \) EXEMPLO

Representação matricial do operador quadrado do operador do momento angular orbital, para \(l=1\):

\[ \boldsymbol{L} ^2 = \begin{array}{ccc} \begin{matrix} m \rightarrow \end{matrix} & \begin{matrix} \hspace{14pt}1 & \hspace{9pt}0 & \hspace{6pt}-1 & \end{matrix} & \begin{matrix} {} \end{matrix} \\ \begin{matrix} \hspace{7pt} 1 \\ \hspace{7pt} 0 \\ -1 \end{matrix} & \begin{bmatrix} 2\hbar^2 & 0 & 0 \\ 0 & 2\hbar^2 & 0 \\ 0 & 0 & 2\hbar^2 \end{bmatrix} & \begin{matrix} {} \end{matrix} \\ \begin{matrix} \uparrow m' \end{matrix} & \begin{matrix} {} \end{matrix} & \begin{matrix} {} \end{matrix} \end{array} \tag{7.10} \]

\[ \boldsymbol{L} ^2 = 2 \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \hbar^2 . \hspace{65pt}{} \tag{7.11} \]

Representação matricial do operador da componente \(z\) do operador do momento angular orbital, para \(l=1\):

\[ \hat{L} _ z = \begin{array}{ccc} \begin{matrix} m \rightarrow \end{matrix} &\begin{matrix} \hspace{10pt}1 & \hspace{2pt}0 & \hspace{2pt}-1 & \end{matrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \hspace{7pt} 1 \\ \hspace{7pt} 0 \\ -1 \end{matrix} &\begin{bmatrix} \hbar & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -\hbar \end{bmatrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \uparrow m' \end{matrix} &\begin{matrix} {} \end{matrix} &\begin{matrix} {} \end{matrix} \end{array} \tag{7.12} \]

\[ \hat{L} _ z = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{bmatrix} \hbar . \hspace{50pt}{} \tag{7.13} \]

Representação matricial do operador de levantamento, para \(l=1\):

\[ \hat{L} _ + = \begin{array}{ccc} \begin{matrix} m \rightarrow \end{matrix} &\begin{matrix} \hspace{6pt}1 & \hspace{9pt}0 & \hspace{6pt}-1 & \end{matrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \hspace{7pt} 1 \\ \hspace{7pt} 0 \\ -1 \end{matrix} &\begin{bmatrix} 0 & \hbar\sqrt{2} & 0 \\ 0 & 0 & \hbar\sqrt{2} \\ 0 & 0 & 0 \end{bmatrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \uparrow m' \end{matrix} &\begin{matrix} {} \end{matrix} &\begin{matrix} {} \end{matrix} \end{array} \tag{7.14} \]

\[ \hat{L} _ + = \sqrt{2} \begin{bmatrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{bmatrix} \hbar . \hspace{50pt}{} \tag{7.15} \]

Representação matricial do operador de abaixamento, para \(l=1\):

\[ \hat{L} _ - = \begin{array}{ccc} \begin{matrix} m \rightarrow \end{matrix} &\begin{matrix} \hspace{22pt}1 & \hspace{12pt}0 & \hspace{4pt}-1 & \end{matrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \hspace{7pt} 1 \\ \hspace{7pt} 0 \\ -1 \end{matrix} &\begin{bmatrix} 0 & 0 & 0 \\ \hbar\sqrt{2} & 0 & 0 \\ 0 & \hbar\sqrt{2} & 0 \end{bmatrix} &\begin{matrix} {} \end{matrix} \\ \begin{matrix} \uparrow m' \end{matrix} &\begin{matrix} {} \end{matrix} &\begin{matrix} {} \end{matrix} \end{array} \]

\[ \hat{L} _ - = \sqrt{2} \begin{bmatrix} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{bmatrix} \hbar . \hspace{60pt}{} \tag{7.16} \]

Por meio da definição (7.3), representação matricial do operador da componente \(x\) do operador do momento angular orbital, para \(l=1\):

\[ \hat{L} _ x = \frac{\sqrt{2}}{2} \begin{bmatrix} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{bmatrix} \hbar . \tag{7.17} \]

Por meio da definição (7.3), representação matricial do operador da componente \(y\) do operador do momento angular orbital, para \(l=1\),

\[ \hat{L} _ y = \frac{\sqrt{2}}{2i} \begin{bmatrix} 0 & 1 & 0 \\ -1 & 0 & 1 \\ 0 & -1 & 0 \end{bmatrix} \hbar . \tag{7.18} \]