1 Introdução

A expansão em série de Taylor no espaço tridimensional é construída pelos vetores de partida \(\vec{r}\), de estudo \(\vec{R}\), e de alcance \(\vec{a} = \vec{R} - \vec{r}\) (G B Arfken 2007). A aplicação desta ferramenta matemática se dá quando se deseja determinar uma função na posição de estudo \(\vec{R}\), aproximando a função em \(1^a\) ordem de expansão, ou \(2^a\), ou \(3^a\), ou quantas ordens for necessário. Por exemplo, o modelo vibracional harmônico aproxima a função de energia potencial por uma função parabólica, de \(2^a\) ordem. Já o modelo vibracional anarmônico, aproxima a energia potencial por uma função de \(3^a\) ordem. Outra situação que necessita de certa expansão em \(1^a\) ordem, é o caso das rotações infinitesimais, em especial, das rotações infinitesimais para se deduzir as componentes do operador do momento angular orbital.

Há duas maneiras de se discutir o momento angular orbital na mecânica quântica (Thompson 1994). Uma, usa a definição do momento angular orbital clássico, a saber, o produto vetorial da posição da partícula pelo seu momento linear, em seguida, faz-se a conversão dos elementos clássicos pelos operadores da posição e do momento linear, fazendo surgir o operador do momento angular orbital — neste ponto, geralmente demonstra-se que as componentes deste operador não comutam entre si. A outra, utiliza as propriedades geométricas das rotações e, assim, deduz-se diretamente o operador do momento angular orbital, sem a necessidade de se lançar mão da definição clássica. Por ser um processo exclusivamente geométrico, pode-se chamar o momento angular resultante desse processo de momento angular geométrico: um momento angular genuinamente angular — uma função pura de ângulos e derivadas de ângulos, quando escrito em coordenadas esféricas, por exemplo. Por fim, faz-se a conexão do momento angular orbital da geometria com o momento angular orbital da mecânica quântica, acrescentando a constante de Planck ao momento angular orbital geométrico.

Neste artigo, vamos deduzir o operador do momento angular associado a uma função espacial e a um campo de vetores, apenas utilizando argumentos geométricos em conjunto com a técnica da expansão em série de Taylor.

2 A notação adotada

Notação \(\eqref{eq:MAX1aa}\):

\[\begin{equation} \text{Coordenadas } (x,y,z) = (x _ 1,x _ 2,x _ 3) . \label{eq:MAX1aa} \end{equation}\]

Notação \(\eqref{eq:MAX1bb}\):

\[\begin{equation} \text{Vetores unit}\acute{\rm a}\text{rios } ( \hat{x} , \hat{y} , \hat{z} ) = ( \hat{x} _ 1 , \hat{x} _ 2 , \hat{x} _ 3 ) . \label{eq:MAX1bb} \end{equation}\]

Notação \(\eqref{eq:MAX1}\):

\[\begin{equation} \text{Vetor } \vec{a} = a _ 1 \hat{x} _ 1 + a _ 2 \hat{x} _ 2 + a _ 3 \hat{x} _ 3 . \label{eq:MAX1} \end{equation}\]

Notação \(\eqref{eq:MAX2}\):

\[\begin{equation} \text{Operador } \vec{\nabla} = \frac{\partial \quad}{\partial x _ 1} \hat{x} _ 1 + \frac{\partial \quad}{\partial x _ 2} \hat{x} _ 2 + \frac{\partial \quad}{\partial x _ 3} \hat{x} _ 3 . \label{eq:MAX2} \end{equation}\]

Notação \(\eqref{eq:MAX3}\):

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right) = a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 3 \frac{\partial \quad}{\partial x _ 3} . \label{eq:MAX3} \end{equation}\]

Notação \(\eqref{eq:MAX4}\):

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right) = \sum _ {\mu} a _ \mu \frac{\partial \quad}{\partial x _ \mu} . \label{eq:MAX4} \end{equation}\]

Notação \(\eqref{eq:MAX5}\):

\[\begin{equation} \sum _ {\mu} = \sum _ {\mu=1}^{3} \label{eq:MAX5} \end{equation}\]

Notação \(\eqref{eq:MAX6}\):

\[\begin{align} \left(\vec{a} \cdot \vec{\nabla} \right)^2 &= \left(\vec{a} \cdot \vec{\nabla} \right) \left(\vec{a} \cdot \vec{\nabla} \right) \notag \\ &= \left(a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 3 \frac{\partial \quad}{\partial x _ 3} \right) \left(a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 3 \frac{\partial \quad}{\partial x _ 3} \right) . \label{eq:MAX6} \end{align}\]

Notação \(\eqref{eq:MAX7}\):

\[\begin{align} \left(\vec{a} \cdot \vec{\nabla} \right)^2 = &\ a _ 1 \frac{\partial \quad}{\partial x _ 1} a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 1 \frac{\partial \quad}{\partial x _ 1} a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 1 \frac{\partial \quad}{\partial x _ 1} a _ 3 \frac{\partial \quad}{\partial x _ 3} \notag \\ +&\ a _ 2 \frac{\partial \quad}{\partial x _ 2} a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 2 \frac{\partial \quad}{\partial x _ 2} a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 2 \frac{\partial \quad}{\partial x _ 2} a _ 3 \frac{\partial \quad}{\partial x _ 3} \notag \\ +&\ a _ 3 \frac{\partial \quad}{\partial x _ 3} a _ 1 \frac{\partial \quad}{\partial x _ 1} + a _ 3 \frac{\partial \quad}{\partial x _ 3} a _ 2 \frac{\partial \quad}{\partial x _ 2} + a _ 3 \frac{\partial \quad}{\partial x _ 3} a _ 3 \frac{\partial \quad}{\partial x _ 3} . \label{eq:MAX7} \end{align}\]

Notação \(\eqref{eq:MAX8}\):

\[\begin{align} \left(\vec{a} \cdot \vec{\nabla} \right)^2 = &\ a _ 1 a _ 1 \frac{\partial ^2 \quad}{\partial x _ 1 \partial x _ 1} + a _ 1 a _ 2 \frac{\partial ^2 \quad}{\partial x _ 1 \partial x _ 2} + a _ 1 a _ 3 \frac{\partial ^2 \quad}{\partial x _ 1 \partial x _ 3} \notag \\ +&\ a _ 2 a _ 1 \frac{\partial ^2 \quad}{\partial x _ 2 \partial x _ 1} + a _ 2 a _ 2 \frac{\partial ^2 \quad}{\partial x _ 2 \partial x _ 2} + a _ 2 a _ 3 \frac{\partial ^2 \quad}{\partial x _ 2 \partial x _ 3} \notag \\ +&\ a _ 3 a _ 1 \frac{\partial ^2 \quad}{\partial x _ 3 \partial x _ 1} + a _ 3 a _ 2 \frac{\partial ^2 \quad}{\partial x _ 3 \partial x _ 2} + a _ 3 a _ 3 \frac{\partial ^2 \quad}{\partial x _ 3 \partial x _ 3} . \label{eq:MAX8} \end{align}\]

Notação \(\eqref{eq:MAX9}\):

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right)^2 = \sum _ {\mu , \nu} a _ \mu a _ \nu \frac{\partial ^2 \quad}{\partial x _ \mu \partial x _ \nu} . \label{eq:MAX9} \end{equation}\]

Notação \(\eqref{eq:MAX10}\):

\[\begin{equation} \sum _ {\mu , \nu} = \sum _ {\mu=1}^{3} \sum _ {\nu=1}^{3} . \label{eq:MAX10} \end{equation}\]

3 Os vetores de trabalho

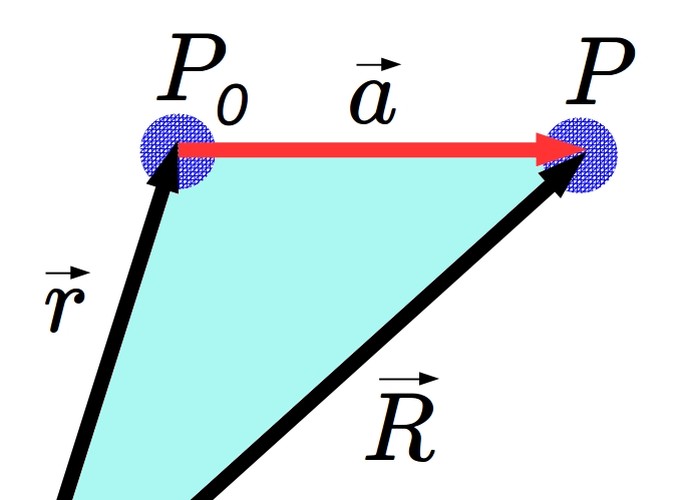
Os vetores utilizados para se escrever uma função em série de Taylor são ilustrados na Figura 3.1. Escolhemos a seguinte notação para eles:

\[\begin{align} \text{O vetor de estudo }{\rm \acute{e}} \! &:\ \vec{R} = X _ 1 \hat{x} _ 1 + X _ 2 \hat{x} _ 2 + X _ 3 \hat{x} _ 3 \hspace{1,00cm} [ \, {\rm Ponto} \ P \, ]; \notag\\ \text{O vetor de partida }{\rm \acute{e}} \! &:\ \vec{r} = x _ 1 \hat{x} _ 1 + x _ 2 \hat{x} _ 2 + x _ 3 \hat{x} _ 3 \hspace{1.60cm} [ \, {\rm Ponto} \ P _ 0 \, ]; \notag\\ \text{E o vetor de alcance }{\rm \acute{e}} \! &:\ \vec{a} = (X _ 1 - x _ 1) \hat{x} _ 1 + (X _ 2 - x _ 2) \hat{x} _ 2 + (X _ 3 - x _ 3) \hat{x} _ 3 . \notag \end{align}\]

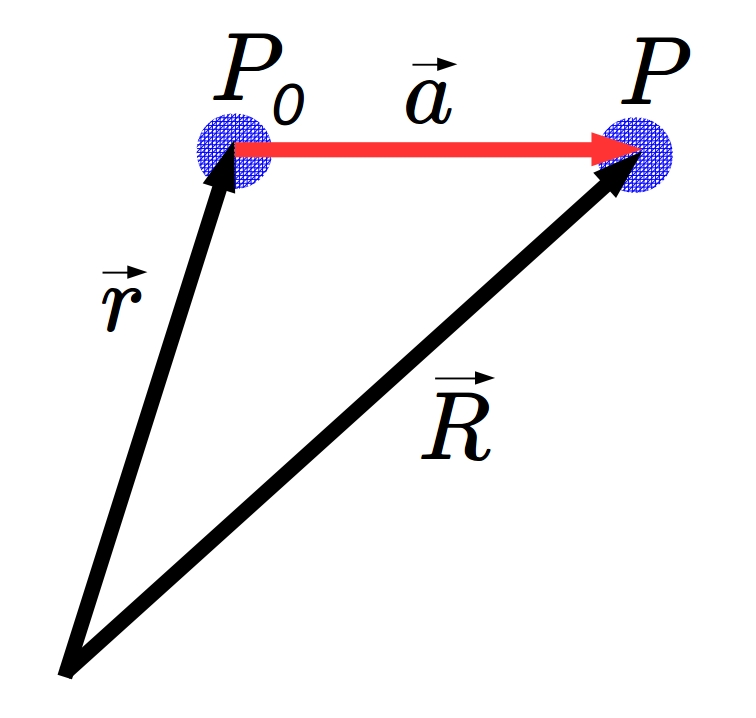
Figura 3.1: O vetor de alcance é: \(\vec{a}=\vec{R} - \vec{r}\).

4 A expansão em série de Taylor

A função na posição de partida possui três variáveis independentes:

\[\begin{equation} V(\vec{r}) \ = \ V (x _ 1 , x _ 2 , x _ 3) . \end{equation}\]

A função na posição de estudo também vai possuir três variáveis independentes, que precisam ser determinadas:

\[\begin{equation} V(\vec{R}) \ = \ V (X _ 1 , X _ 2 , X _ 3) . \end{equation}\]

A função na posição de estudo, a ser determinada pela função na posição de partida, será determinada por uma expansão em série de Taylor da função na posição de partida. Será uma expansão em torno de \(\vec{r}\), com alcance \(\vec{a}\), escrita na forma:

\[\begin{equation} V(\vec{R}) \ = \ V(\vec{r}) \ + \ \left(\vec{a} \cdot \vec{\nabla} \right) V(\vec{r}) \ + \ \frac{1}{2!} \left(\vec{a} \cdot \vec{\nabla} \right)^2 V(\vec{r}) \ + \ \dots \label{eq:MAX12} \end{equation}\]

Nota: Em torno de \(\vec{r}\) significa dizer que a expansão vai ocorrer ao redor do ponto \(P_0\) da Figura 3.1.

Termo 1 da expansão:

\[\begin{equation} V(\vec{r}) \ = \ V \Bigg| _ {P _ 0} \label{eq:MAX13} \end{equation}\]

Termo 2 da expansão:

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right) V(\vec{r}) \ = \ \sum _ {\mu} a _ \mu \frac{\partial V}{\partial x _ \mu} \Bigg| _ {P _ 0} \label{eq:MAX14} \end{equation}\]

Termo 3 da expansão:

\[\begin{equation} \frac{1}{2!} \left(\vec{a} \cdot \vec{\nabla} \right)^2 V(\vec{r}) \ = \ \frac{1}{2} \sum _ {\mu , \nu} a _ \mu a _ \nu \frac{\partial ^2 V}{\partial x _ \mu \partial x _ \nu} \Bigg| _ {P _ 0} \label{eq:MAX15} \end{equation}\]

Notação compacta da expansão em série de Taylor \(\eqref{eq:MAX12}\) (G B Arfken 2007):

\[\begin{equation} V(\vec{R}) \ = \ \sum _ {n=0} ^{\infty} \frac{1}{n!} \left(\vec{a} \cdot \vec{\nabla} \right)^n V(\vec{r}) . \label{eq:MAX16} \end{equation}\]

5 A expansão em uma única dimensão

Redução do sistema de coordenadas:

\[\begin{equation} (x _ 1 , x _ 2 , x _ 3) \ \to \ (x _ 1, 0 , 0) = (x , 0 , 0) \end{equation}\]

Redução dos vetores de trabalho:

\[\begin{align} \vec{R} = (X _ 1 , X _ 2 , X _ 3) \ &\to \ \vec{R} = (X _ 1 , 0 , 0) = (x , 0 , 0) \notag\\ \vec{r} = (x _ 1 , x _ 2 , x _ 3) \ &\to \ \vec{r} = (x _ 1 , 0 , 0) = (x _ 0 , 0 , 0) \notag\\ \vec{a} = (a _ 1 , a _ 2 , a _ 3) \ &\to \ \vec{a} = (a _ 1 , 0 , 0) = (x - x _ 0 , 0 , 0) \end{align}\]

Redução da equação \(\eqref{eq:MAX14}\):

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right) V(\vec{r}) \ = \ a _ 1 \frac{\partial V}{\partial x _ 1} \Bigg| _ {P _ 0} \label{eq:MAX14b} \end{equation}\]

Redução da equação \(\eqref{eq:MAX15}\):

\[\begin{equation} \frac{1}{2!} \left(\vec{a} \cdot \vec{\nabla} \right)^2 V(\vec{r}) \ = \ \frac{1}{2} a _ 1^2 \frac{\partial ^2 V}{\partial x _ 1^2} \Bigg| _ {P _ 0} \label{eq:MAX15b} \end{equation}\]

Então, a expansão em torno do \(\vec{r} = (x _ 0 , 0 , 0)\), com alcance \(\vec{a} = (x - x _ 0 , 0 , 0)\), é:

\[\begin{equation} V(x) \ = \ V(x _ 0) \ + \ (x - x _ 0) \frac{\partial V}{\partial x} \Bigg| _ {x _ 0} \ + \ \frac{1}{2} (x - x _ 0)^2 \frac{\partial ^2 V}{\partial x^2} \Bigg| _ {x _ 0} \ + \ \dots \end{equation}\]

Agora, a expansão em torno do \(\vec{r} = (0 , 0 , 0)\), quer dizer, em torno da origem, com alcance \(\vec{a} = (x , 0 , 0)\), é:

\[\begin{equation} V(x) \ = \ V(0) \ + \ x \frac{\partial V}{\partial x} \Bigg| _ {0} \ + \ \frac{1}{2} x^2 \frac{\partial ^2 V}{\partial x^2} \Bigg| _ {0} \ + \ \dots \end{equation}\]

6 O momento angular orbital deduzido por geometria

Considere uma rotação infinitesimal de um vetor no espaço, no sentido horário, de ângulo \(\delta = -\varepsilon _ z\), e em torno do eixo principal \(z\). Considere que os vetores de partida e de estudo que aparecem na Figura 3.1 \((\vec{r},\vec{R})\) representem o início e o fim dessa rotação. Nesse caso, suas componentes estarão relacionadas através da matriz de rotação \(R( \delta , \hat{\boldsymbol{\rm z}} )\), da seguinte maneira:

\[\begin{equation}\label{eq:ROT1} \vec{R} = R( -\varepsilon _ z , \hat{\boldsymbol{\rm z}} ) \vec{r} . \end{equation}\]

Em termos matriciais:

\[\begin{equation}\label{eq:ROT2} \begin{bmatrix} X _ 1 \\ X _ 2 \\ X _ 3 \end{bmatrix} = \begin{bmatrix} \cos(-\varepsilon _ z) & -\sin(-\varepsilon _ z) & 0 \\ \sin(-\varepsilon _ z) & \cos(-\varepsilon _ z) & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x _ 1 \\ x _ 2 \\ x _ 3 \end{bmatrix} \end{equation}\]

Como as rotações são infinitesimais, pode-se usar as aproximações \(\sin \theta \approx \theta\) e \(\cos \theta \approx 1\) na equação \(\eqref{eq:ROT2}\):

\[\begin{equation}\label{eq:ROT3} \begin{bmatrix} X _ 1 \\ X _ 2 \\ X _ 3 \end{bmatrix} = \begin{bmatrix} 1 & \varepsilon _ z & 0 \\ -\varepsilon _ z & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x _ 1 \\ x _ 2 \\ x _ 3 \end{bmatrix} \end{equation}\]

A solução da equação \(\eqref{eq:ROT3}\) é:

\[\begin{equation} \begin{aligned} X _ 1 &= x _ 1 + \varepsilon _ z x _ 2 \\ X _ 2 &= -\varepsilon _ z x _ 1 + x _ 2 \\ X _ 3 &= x _ 3 \end{aligned} \label{eq:ROT4} \end{equation}\]

Isto posto, monta-se o vetor rodado:

\[\begin{equation} \vec{R} = ( x _ 1 + \varepsilon _ z x _ 2 ) \hat{x} _ 1 + ( -\varepsilon _ z x _ 1 + x _ 2 ) \hat{x} _ 2 + x _ 3 \hat{x} _ 3 . \label{eq:ROT5a} \end{equation}\]

De antemão, sabe-se o vetor de partida:

\[\begin{equation} \vec{r} = x _ 1 \hat{x} _ 1 + x _ 2 \hat{x} _ 2 + x _ 3 \hat{x} _ 3 . \label{eq:ROT5b} \end{equation}\]

Então, subtraindo \(\eqref{eq:ROT5a}\) de \(\eqref{eq:ROT5b}\), determina-se o vetor de alcance:

\[\begin{equation} \vec{a} = (\varepsilon _ z x _ 2 ) \hat{x} _ 1 + (-\varepsilon _ z x _ 1) \hat{x} _ 2 + ( 0 ) \hat{x} _ 3 . \label{eq:ROT5c} \end{equation}\]

Ao substituir as componentes do vetor de alcance na equação \(\eqref{eq:MAX3}\), obtém-se:

\[\begin{equation} \left(\vec{a} \cdot \vec{\nabla} \right) = (\varepsilon _ z x _ 2 ) \frac{\partial \quad}{\partial x _ 1} + (-\varepsilon _ z x _ 1) \frac{\partial \quad}{\partial x _ 2} + (0) \frac{\partial \quad}{\partial x _ 3} . \label{eq:ROT6} \end{equation}\]

Conhecendo a técnica da expansão em série de Taylor \(\eqref{eq:MAX12}\), um vetor de estado (o mesmo que uma função espacial que descreve um sistema quântico), na posição do vetor rodado, é assim escrito tendo em conta apenas a \(1^a\) ordem da expansão:

\[\begin{equation} \Psi(\vec{R}) = \Psi(\vec{r}) + \varepsilon _ z \left( x _ 2 \frac{\partial \quad}{\partial x _ 1} - x _ 1 \frac{\partial \quad}{\partial x _ 2} \right) \Psi(\vec{r}) + \dots \label{eq:ROT7} \end{equation}\]

Enfatizando, na \(\eqref{eq:ROT7}\) temos o vetor de estado (na posição do vetor rodado) escrito em função do vetor de estado (na posição do vetor de partida).

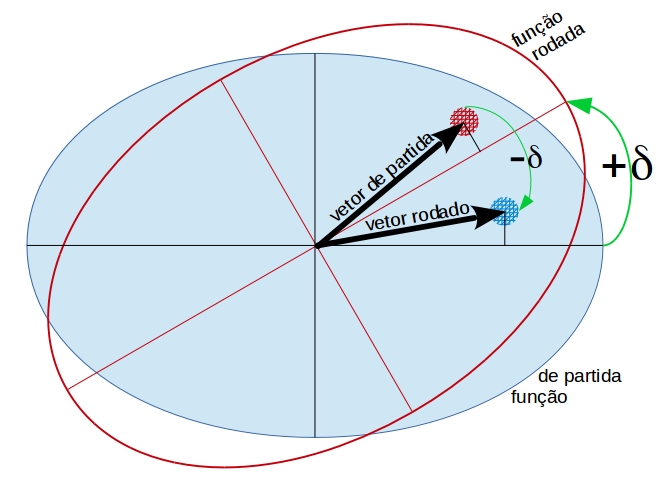
Figura 6.1: Ilustração do processo de rotação de uma função espacial. Na região hachurada, o valor da função rodada, computado na posição do vetor de partida, é igual ao valor da função de partida, computado na posição do vetor rodado.

Além de vetores, a matriz de rotação realiza rotações de funções. Um conceito geométrico rotacional estabelece que a rotação de funções também pode ser realizada pelo operador rotacional \(U\).

Nota: \(U\), de unitário, por se tratar de um operador representado por uma matriz unitária (matriz que preserva a norma da operação).

O operador rotacional pode ser escrito como exponencial do operador do momento angular geométrico (Thompson 1994). No caso em questão, como se deseja uma rotação em torno do eixo \(z\), se escreve em função da componente \(z\) do operador do momento angular orbital:

\[\begin{equation} U( \varepsilon _ z , \hat{\boldsymbol{\rm z}} ) = e^{-i\varepsilon _ z L _ z} . \label{eq:ROT8} \end{equation}\]

O operador de rotação aplicado na função de onda original (de partida) gera a função de onda rodada:

\[\begin{equation} \Psi _ {\rm rod}(\vec{r}) = U( \varepsilon _ z , \hat{\boldsymbol{\rm z}} ) \Psi(\vec{r}) . \label{eq:ROT11} \end{equation}\]

Aqui vamos recordar como se expande uma exponencial:

\[\begin{equation} e^P = P^0 + \frac{P^1}{1!} + \frac{P^2}{2!} + \frac{P^3}{3!} +\dots \label{eq:ROT9} \end{equation}\]

Utilizando \(\eqref{eq:ROT9}\) em \(\eqref{eq:ROT8}\), obtém-se:

\[\begin{equation} U( \varepsilon _ z , \hat{\boldsymbol{\rm z}} ) = 1 -i\varepsilon _ z L _ z -\frac{\varepsilon _ z^2 L _ z^2}{2} + \dots \label{eq:ROT10} \end{equation}\]

Então, em aproximação de \(1^a\) ordem, a equação \(\eqref{eq:ROT11}\) se torna:

\[\begin{equation} \Psi _ {\rm rod}(\vec{r}) = \left( 1 -i\varepsilon _ z L _ z \right) \Psi(\vec{r}) . \label{eq:ROT12} \end{equation}\]

Acompanhe a Figura 6.1: O valor da função de onda rodada, computado na posição do vetor de partida, é igual ao valor da função de onda de partida, computado na posição do vetor rodado no sentido contrário (Thompson 1994):

\[\begin{equation} \Psi _ {\rm rod}(\vec{r}) = \Psi(\vec{R}) \ \ \xleftarrow[\text{\eqref{eq:ROT7}}]{\text{Eq.}} \ \ \\ \Psi _ {\rm rod}(\vec{r}) = \Psi(\vec{r}) + \varepsilon _ z \left( x _ 2 \frac{\partial \quad}{\partial x _ 1} - x _ 1 \frac{\partial \quad}{\partial x _ 2} \right) \Psi(\vec{r}) + \dots \label{eq:ROT12b} \end{equation}\]

Agora, igualando as equações \(\eqref{eq:ROT12}\) e \(\eqref{eq:ROT12b}\), obtém-se:

\[\begin{equation} \begin{aligned} \left( 1 -i\varepsilon _ z L _ z \right) \Psi(\vec{r}) &= \Psi(\vec{r}) + \varepsilon _ z \left( x _ 2 \frac{\partial \quad}{\partial x _ 1} - x _ 1 \frac{\partial \quad}{\partial x _ 2} \right) \Psi(\vec{r}) \\ \implies -i L _ z &= \left( x _ 2 \frac{\partial \quad}{\partial x _ 1} - x _ 1 \frac{\partial \quad}{\partial x _ 2} \right) . \end{aligned} \label{eq:ROT13} \end{equation}\]

Logo, a componente \(z\) do operador do momento angular orbital geométrico é expressa como:

\[\begin{equation} { L _ z = -i \left( x _ 1 \frac{\partial \quad}{\partial x _ 2} - x _ 2 \frac{\partial \quad}{\partial x _ 1} \right) . } \end{equation}\]

O procedimento é cíclico, quer dizer, pode-se fazer a substituição cíclica dos rótulos dos eixos para se determinar as outras componentes:

\[\begin{equation} { L _ x = -i \left( x _ 2 \frac{\partial \quad}{\partial x _ 3} - x _ 3 \frac{\partial \quad}{\partial x _ 2} \right) . } \end{equation}\]

\[\begin{equation} { L _ y = -i \left( x _ 3 \frac{\partial \quad}{\partial x _ 1} - x _ 1 \frac{\partial \quad}{\partial x _ 3} \right) . } \end{equation}\]

Ao representar o sistema de coordenadas Carteziano na forma tradicional, as componentes do operador do momento angular orbital geométrico são expressas como:

\[\begin{equation} \bbox[yellow, 12px]{ L _ z = -i \left( x \frac{\partial \quad}{\partial y} - y \frac{\partial \quad}{\partial x} \right) } \notag \end{equation}\]

\[\begin{equation} \bbox[yellow, 12px]{ L _ x = -i \left( y \frac{\partial \quad}{\partial z} - z \frac{\partial \quad}{\partial y} \right) } \notag \end{equation}\]

\[\begin{equation} \bbox[yellow, 12px]{ L _ y = -i \left( z \frac{\partial \quad}{\partial x} - x \frac{\partial \quad}{\partial z} \right) } \notag \end{equation}\]

6.1 Figuras complementares

A ilustração 6.1 foi construída com as funções sobrepostas (de partida e rodada). Uma visão alternativa é apresentada na ilustração 6.2, onde as funções são afastadas. A função rodada pelo ângulo \(\varepsilon\), função \(f_{\varepsilon}(x,y)\), é gerada pela aplicação do operador de rotação na função original, operação \(U(\varepsilon,z)f(x,y)\), e o resultado dessa operação, é igual à função original na posição rodada pelo ângulo \((-\varepsilon)\), função \(f(x_{-\varepsilon},y_{-\varepsilon})\). A análise do processo é feita com os eixos cartesianos fixos.

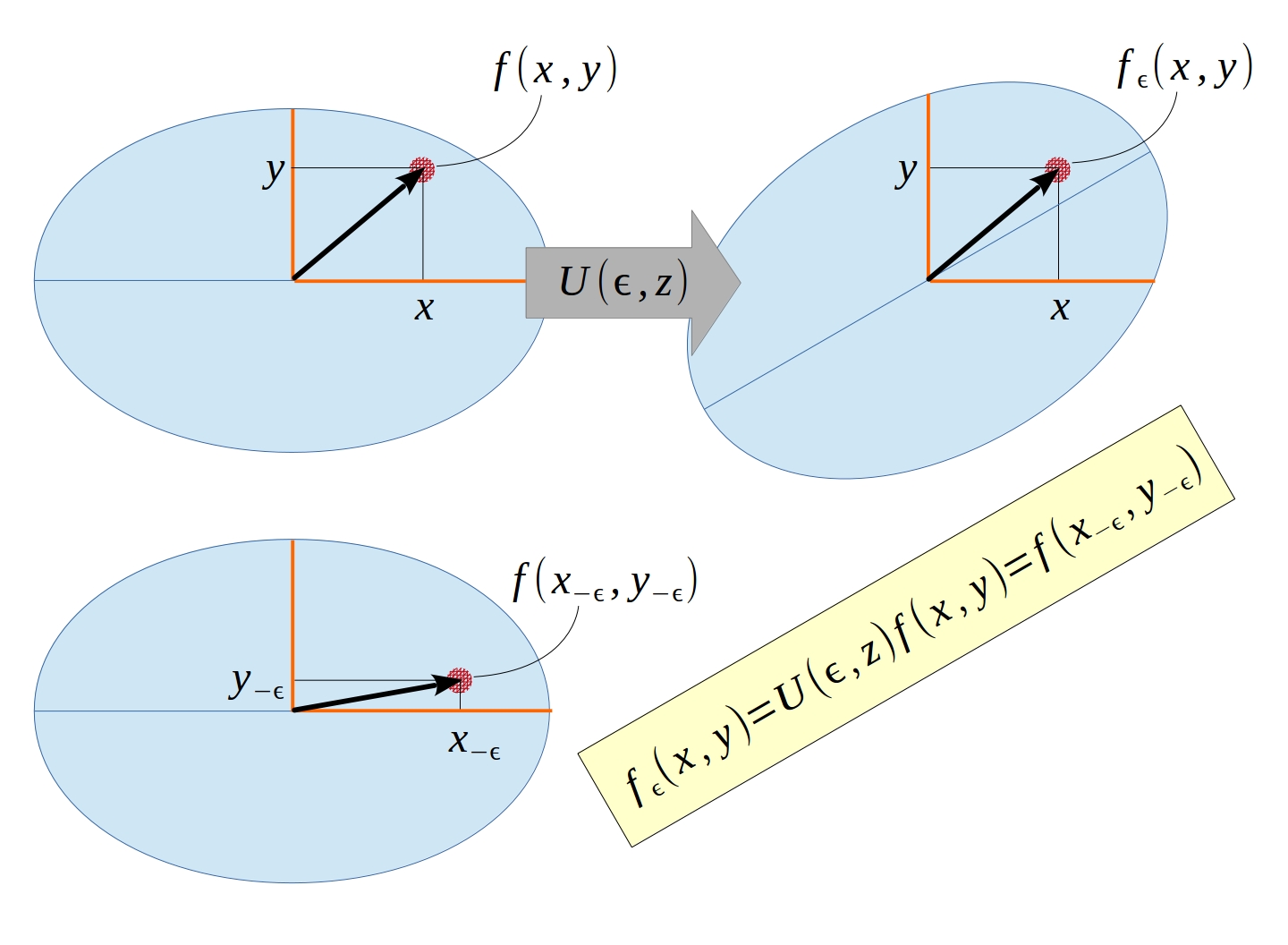
Figura 6.2: Ilustração do processo de rotação de uma função espacial genérica.

Uma ilustração tem caráter didático. As ilustrações 6.1 e 6.2 ilustram o processo de rotação de uma função espacial genérica: uma função qualquer que é função exclusiva das coordenadas \((xyz)\). Uma ilustração com caráter realístico-didático, pode ser construída com uma função matemática que tenha conexão com a realidade.

A Figura 6.3 é construída com o módulo ao quadrado do harmônico esférico \(Y_{10}(\theta \phi)\), o que tem a ver com a probabilidade de se encontrar uma partícula com momento angular \(l=1\) e projeção \(m=0\), na posição angular \(\theta\) — ao fazer o módulo ao quadrado, cancela-se a denpendência da posição ângular \(\phi\). Utilizou-se a técnica da plotagem polar: Os valores de uma função \(f(\phi)\) são anexados a um raio \(R\), ou seja, faz-se \(R=f(\phi)\). No eixo \(x\), são anexados os valores de \(R{\rm cos}(\phi)\), e no eixo \(y\), os valores de \(R{\rm sen}(\phi)\). Ao fazer a varredura do ângulo \(\phi\), o raio desenha a curva de \(f\) pelo espaço. Para descrever a função rodada, o ângulo \(\epsilon\) foi acrescentado à expressão do harmônico esférico, resultando na densidade de probabilidade \(\eqref{eq:d1}\).

\[\begin{equation}\label{eq:d1} |Y _ {10}|^2 = \frac{3}{4\pi} {\rm cos}^2 (\phi - \epsilon) . \end{equation}\]

A ilustração realístico-didático 6.3 reforça o entendimento que a função rodada, na posição de partida, \(f_\epsilon(\vec{r})\), é igual à função de partica, na posição rodada no sentido contrário, \(f(\vec{r}_{\! -\epsilon})\). — Argumento explorado no passo \(\eqref{eq:ROT12b}\).

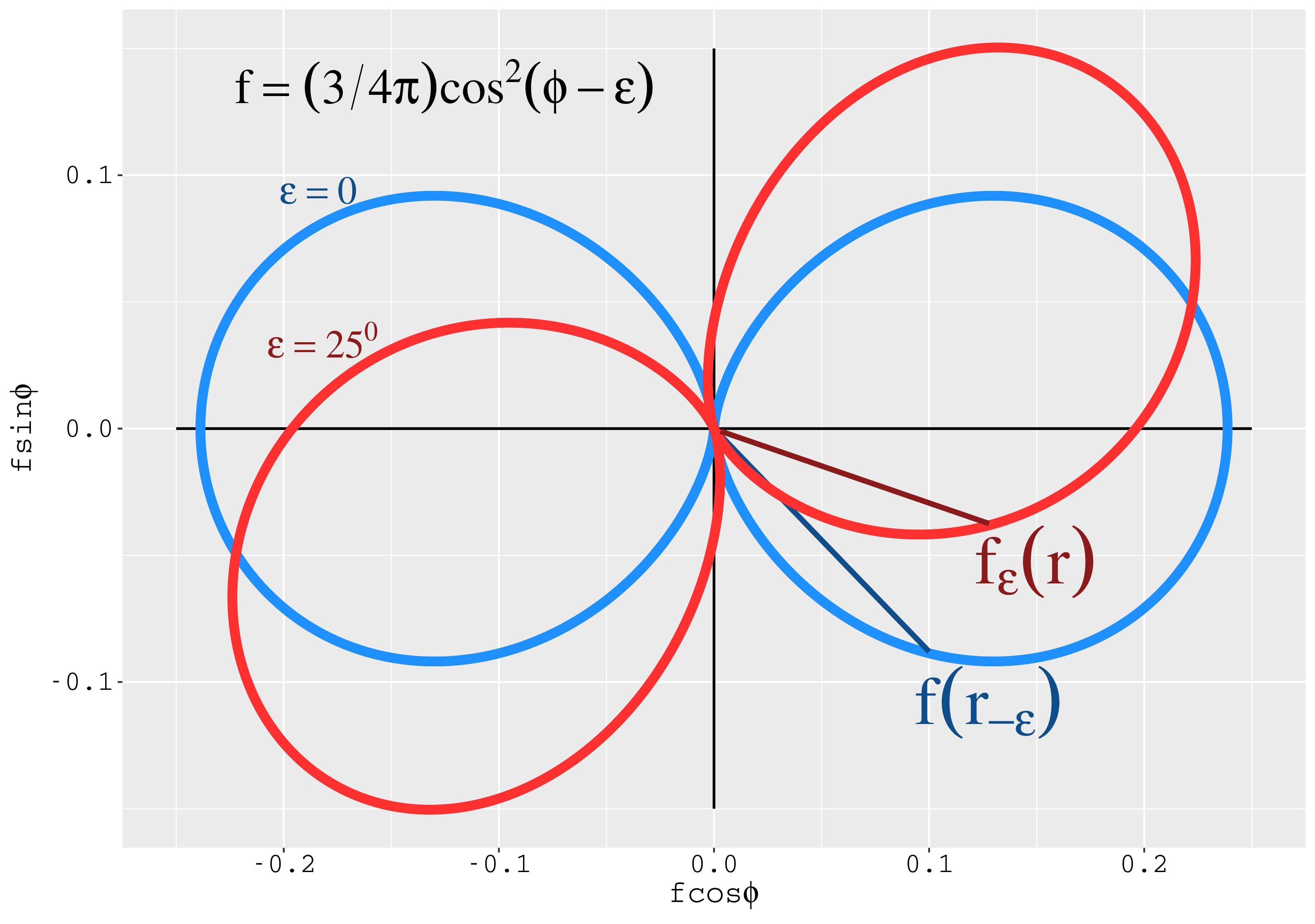
Figura 6.3: Rotação da densidade de probabilidade decorrente do harmônico esférico_10.

Até este momento, deduzimos o operador que descreve rotações infinitesimais de funções espaciais: o operador do momento angular orbital. É oportuno expandir a pesquisa para saber qual é o operador que se associa a um campo de vetores em rotação infinitesimal.

7 O momento angular de um campo de vetores

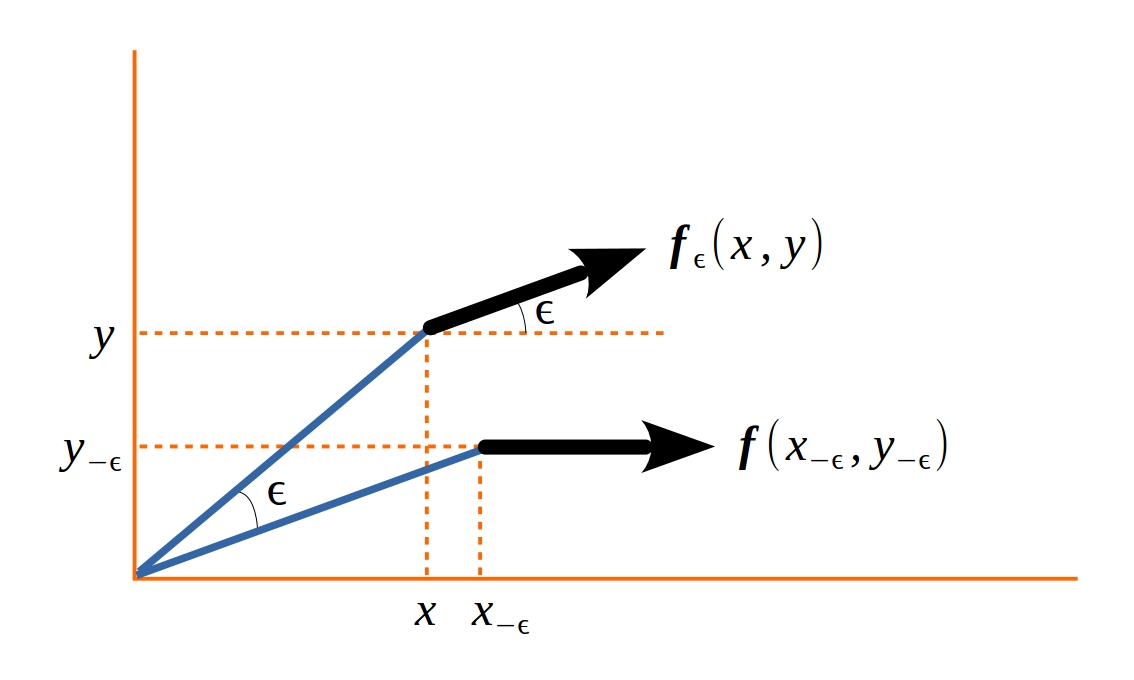
Figura 7.1: Ilustração do processo de rotação de um campo vetorial.

A Figura 7.1 vai nos auxiliar na busca do operador que se associa a um campo de vetores em rotação infinitesimal. Um campo vetorial é formado por vetores do tipo \(\boldsymbol{f}(xyz)=\left(\,f_x(xyz),\ f_y(xyz),\ f_z(xyz)\,\right)\) — correndo os valores de \((xyz)\). Como se vê, o vetor \(\boldsymbol{f}(x_{-\varepsilon},y_{-\varepsilon},z_{-\varepsilon})\) é rodado em torno do eixo \(z\) — é rodado pela matriz de rotação \(R_z(\varepsilon)\) — e, após a rotação, se transforma em um novo vetor: no vetor rodado \(\boldsymbol{f}_{\varepsilon}(x,y,z)\). Em termos matemáticos:

\[\begin{equation}\label{eq:mais1} \newcommand{\vv}[1]{\boldsymbol{#1}} R _ z (\varepsilon) \vv{f}(x _ {-\varepsilon},y _ {-\varepsilon},z _ {-\varepsilon}) = \vv{f} _ {\varepsilon}(x,y,z) . \end{equation}\]

A matriz que causa a rotação é definida em \(\eqref{eq:ROT2}\). Para rotações infinitesimais, pode-se usar \(\sin \theta \approx \theta\) e \(\cos \theta \approx 1\). Nesse caso, a matriz de rotação pode ser escrita como:

\[\begin{equation}\label{eq:mais2} R _ z (\varepsilon) = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} + \varepsilon \begin{bmatrix} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \equiv \boldsymbol{\rm 1} + \varepsilon \boldsymbol{\rm M} _ z . \end{equation}\]

O vetor \(\boldsymbol{\rm r}_{-\varepsilon}=(x_{-\varepsilon},y_{-\varepsilon},z_{-\varepsilon})\) também pode ser pensado como o resultado de uma rotação: da rotação do vetor \(\boldsymbol{\rm r}=(x,y,z)\) pelo ângulo \((-\varepsilon\)):

\[\begin{equation}\label{eq:mais3} \begin{bmatrix} x _ {-\varepsilon} \\ y _ {-\varepsilon} \\ z _ {-\varepsilon} \end{bmatrix} = \begin{bmatrix} 1 & \varepsilon & 0 \\ -\varepsilon & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} x \\ y \\ z \end{bmatrix} = \begin{bmatrix} x + \varepsilon y \\ y - \varepsilon x \\ z \end{bmatrix} \end{equation}\]

O resultado \(\eqref{eq:mais3}\) mostra que \(\boldsymbol{f}(x_{-\varepsilon},y_{-\varepsilon},z_{-\varepsilon})\) pode ser expandido em série de Taylor. Levando em conta apenas a \(1^a\) ordem da expansão, tem-se:

\[\begin{equation}\label{eq:mais4} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{f}(x _ {-\varepsilon},y _ {-\varepsilon},z _ {-\varepsilon}) = \vv{f}(x + \varepsilon y,y - \varepsilon x,z) = \vv{f}(x,y,z) + \varepsilon \left( y\frac{\partial \quad}{\partial x} - x\frac{\partial \quad}{\partial y} \right)\vv{f}(x,y,z).\\ \end{equation}\]

No ponto \((x,y,z)\), o operador da rotação aplicado no vetor \(\boldsymbol{f}\) gera o vetor rodado:

\[\begin{equation}\label{eq:mais5} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{f} _ {\varepsilon}(x,y,z) = \left( \vv{1} -i\varepsilon \vv{\rm J} _ z \right) \vv{f}(x,y,z) . \end{equation}\]

Utilizando os resultados \(\eqref{eq:mais2}\), \(\eqref{eq:mais4}\) e \(\eqref{eq:mais5}\), reescreve-se a equação \(\eqref{eq:mais1}\):

\[\begin{equation}\label{eq:mais6} \newcommand{\vv}[1]{\boldsymbol{#1}} \left( \vv{1} + \varepsilon \vv{\rm M} _ z \right) \left( \vv{f}(x,y,z) + \varepsilon \left( y\frac{\partial\quad}{\partial x} - x\frac{\partial\quad}{\partial y} \right) \vv{f}(x,y,z) \right) = \left( \vv{1} -i\varepsilon \boldsymbol{\rm J} _ z \right) \vv{f}(x,y,z) . \end{equation}\]

As próximas passagens tem como objetivo manipular \(\eqref{eq:mais6}\) para se extrair a expressão da componente \(z\) do momento angular do campo de vetores.

Ao fazer a multiplicação do lado esquerdo da \(\eqref{eq:mais6}\), despreza-se o termo que aparece \(\varepsilon^2\):

\[\begin{equation}\label{eq:mais7} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{1} \vv{f}(x,y,z) + \vv{1} \varepsilon \left( y\frac{\partial\quad}{\partial x} - x\frac{\partial\quad}{\partial y} \right) \vv{f}(x,y,z) + \varepsilon \vv{\rm M} _ z \vv{f}(x,y,z) = \left( \vv{1} -i\varepsilon \boldsymbol{\rm J} _ z \right) \vv{f}(x,y,z) . \end{equation}\]

Cancela-se \(\boldsymbol{f}\) da \(\eqref{eq:mais7}\):

\[\begin{equation}\label{eq:mais8} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{1} + \vv{1} \varepsilon \left( y\frac{\partial\quad}{\partial x} - x\frac{\partial\quad}{\partial y} \right) + \varepsilon \vv{\rm M} _ z = \vv{1} -i\varepsilon \boldsymbol{\rm J} _ z . \end{equation}\]

Subtrai-se \(\boldsymbol{1}\) em ambos os lados da \(\eqref{eq:mais8}\):

\[\begin{equation}\label{eq:mais9} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{1} \varepsilon \left( y\frac{\partial\quad}{\partial x} - x\frac{\partial\quad}{\partial y} \right) + \varepsilon \vv{\rm M} _ z = -i\varepsilon \boldsymbol{\rm J} _ z . \end{equation}\]

Cancela-se a ângulo \(\varepsilon\) da \(\eqref{eq:mais9}\):

\[\begin{equation}\label{eq:mais10} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{1} \left( y\frac{\partial\quad}{\partial x} - x\frac{\partial\quad}{\partial y} \right) + \vv{\rm M} _ z = -i \boldsymbol{\rm J} _ z . \end{equation}\]

Inverte-se o parênteses da \(\eqref{eq:mais10}\):

\[\begin{equation}\label{eq:mais11} \newcommand{\vv}[1]{\boldsymbol{#1}} -\vv{1} \left( x\frac{\partial\quad}{\partial y} - y\frac{\partial\quad}{\partial x} \right) + \vv{\rm M} _ z = -i \boldsymbol{\rm J} _ z . \end{equation}\]

Miltiplica-se ambos os lados da \(\eqref{eq:mais11}\) por \(i\):

\[\begin{equation}\label{eq:mais12} \newcommand{\vv}[1]{\boldsymbol{#1}} \boldsymbol{\rm J} _ z = -i \, \vv{1} \left( x\frac{\partial\quad}{\partial y} - y\frac{\partial\quad}{\partial x} \right) + i \vv{\rm M} _ z . \end{equation}\]

Agora, defini-se o a componente \(z\) do operador da rotação intrínseca do campo de vetores – a componente \(z\) do operador de spin:

\[\begin{equation}\label{eq:mais13} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{\rm S} _ z \equiv i\vv{\rm M} _ z = \begin{bmatrix} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Enfim, substituindo \(\eqref{eq:mais13}\) em \(\eqref{eq:mais12}\), tem-se a expressão da componente \(z\) do momento angular do campo de vetores:

\[\begin{equation}\label{eq:mais14a} \newcommand{\vv}[1]{\boldsymbol{#1}} \boldsymbol{\rm J} _ z = -i \! \left( x\frac{\partial\quad}{\partial y} - y\frac{\partial\quad}{\partial x} \right) \! \vv{1} + \vv{\rm S} _ z . \end{equation}\]

Ou, em termos matriciais:

\[\begin{equation}\label{eq:mais14b} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \boldsymbol{\rm J} _ z = \begin{bmatrix} -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 & 0 \\ 0 & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 \\ 0 & 0 & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) \end{bmatrix} + \begin{bmatrix} 0 & -i & 0 \\ i & 0 & 0 \\ 0 & 0 & 0 \end{bmatrix} \end{equation}\]

Por meio de \(\eqref{eq:mais14b}\), escreve-se o operador que causa a rotação em um vetor do campo:

\[\begin{equation}\label{eq:mais14c} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \boldsymbol{\rm U} _ z (\varepsilon) = \vv{1} -i\varepsilon \vv{\rm J} _ z = \begin{bmatrix} 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & -\varepsilon & 0 \\ \varepsilon & 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 \\ 0 & 0 & 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) \end{bmatrix} \end{equation}\]

Então, o resultado da aplicação de \(\eqref{eq:mais14b}\) em um vetor do campo é:

\[\begin{equation}\label{eq:mais14d} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{f} _ \varepsilon = \left(\vv{1} - i\varepsilon \vv{\rm J} _ z\right) \vv{f} = \begin{bmatrix} f _ x-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ x - \varepsilon f _ y\\ f _ y-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ y + \varepsilon f _ x\\ f _ z-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ z \end{bmatrix} . \end{equation}\]

7.1 O momento angular orbital de um campo de vetores

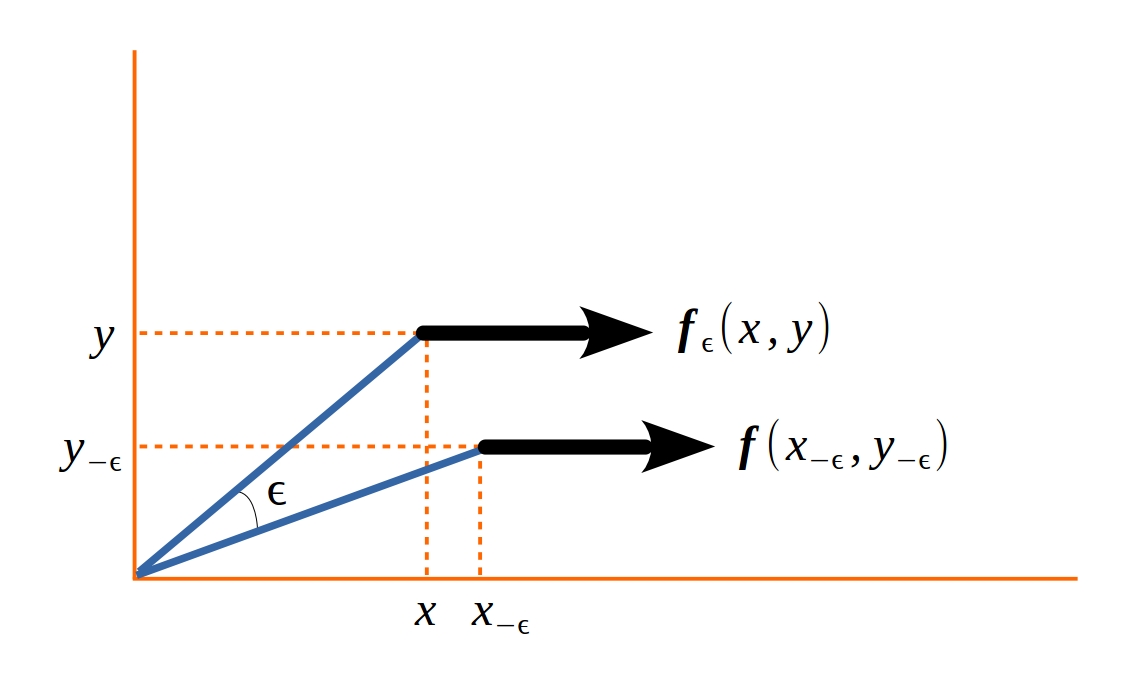
Figura 7.2: Ilustração do processo de rotação de um campo vetorial sem o efeito do spin.

A Figura 7.2 mostra a rotação do vetor \(\boldsymbol{f}(x_{-\varepsilon},y_{-\varepsilon},z_{-\varepsilon})\), em torno do eixo \(z\), mas sem levar em conta o efeito do spin. Nesse caso,

\[\begin{equation}\label{eq:mais15} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{f}(x _ {-\varepsilon},y _ {-\varepsilon},z _ {-\varepsilon}) = \vv{f} _ {\varepsilon}(x,y,z) . \end{equation}\]

Eliminando \(\left(\boldsymbol{1} + \varepsilon\boldsymbol{\rm M}_z\right)\) da equação \(\eqref{eq:mais6}\), a dedução conduz à expressão da componente \(z\) do momento angular orbital do campo de vetores:

\[\begin{equation}\label{eq:mais16a} \newcommand{\vv}[1]{\boldsymbol{#1}} \boldsymbol{\rm L} _ z = -i \! \left( x\frac{\partial\quad}{\partial y} - y\frac{\partial\quad}{\partial x} \right) \! \vv{1} . \end{equation}\]

Ou, em termos matriciais:

\[\begin{equation}\label{eq:mais16b} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \boldsymbol{\rm L} _ z = \begin{bmatrix} -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 & 0 \\ 0 & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 \\ 0 & 0 & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) \end{bmatrix} \end{equation}\]

Por meio de \(\eqref{eq:mais16b}\), escreve-se o operador que causa a rotação-sem-spin em um vetor do campo:

\[\begin{equation}\label{eq:mais16c} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \boldsymbol{\rm U} _ z (\varepsilon) = \vv{1} -i\varepsilon \vv{\rm L} _ z = \begin{bmatrix} 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 & 0 \\ 0 & 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 \\ 0 & 0 & 1-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) \end{bmatrix} \end{equation}\]

Então, o resultado da aplicação de \(\eqref{eq:mais16b}\) em um vetor do campo é:

\[\begin{equation}\label{eq:mais16d} \newcommand{\vv}[1]{\boldsymbol{#1}} \vv{f} _ \varepsilon = \left(\vv{1} - i\varepsilon \vv{\rm L} _ z\right) \vv{f} = \begin{bmatrix} f _ x-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ x \\ f _ y-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ y \\ f _ z-\varepsilon\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right)f _ z \end{bmatrix} \end{equation}\]

A comparação das equações \(\eqref{eq:mais16d}\) e \(\eqref{eq:mais14d}\) mostra que o efeito do spin é misturar as componentes do vetor de partida ao formar o vetor rodado. O efeito do operador-orbital é transformar as componentes do vetor de partida em novas componentes para o vetor rodado, mas mantendo a ordem: a nova componente \(f_x\) do vetor rodado \(\eqref{eq:mais16d}\) só possui transformação de compomente \(f_x\) do vetor de partida. Mas, quando o operador-spin passa a atuar, a nova compomente \(f_x\) do vetor rodado \(\eqref{eq:mais14d}\) também passa a sofrer transformação da compomente \(f_y\) do vetor de partida, o que leva à transformação com mistura de componentes.

E que também leva ao jogo de palavras: — Com spin, com mistura; sem spin, sem mistura.

8 Procedimento alternativo para se determinar o momento angular de um campo de vetores

Rotação do vetor posição (em torno do eixo \(z\), pelo ângulo infinitesimal \(\varepsilon\)):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} \vv{\rm r} _ {\varepsilon} &= R _ z (\varepsilon) \vv{\rm r} \\ &= \begin{bmatrix} 1 & -\varepsilon & 0 \\ \varepsilon & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} {x} \\ {y} \\ {z} \end{bmatrix} \\ &= \begin{bmatrix} {x} -\varepsilon {y} \\ {y} +\varepsilon {x} \\ {z} \end{bmatrix} \end{aligned} \label{eq:alt0} \end{equation}\]

Rotação do campo de vetores:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} \vv{f} _ {\varepsilon} ( \vv{\rm r} _ {\varepsilon} ) &= R _ z (\varepsilon) \vv{f} ( \vv{\rm r} ) \\ &= \begin{bmatrix} 1 & -\varepsilon & 0 \\ \varepsilon & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} {f} _ {x} ( \vv{\rm r} ) \\ {f} _ {y} ( \vv{\rm r} ) \\ {f} _ {z} ( \vv{\rm r} ) \end{bmatrix} \\ &= \begin{bmatrix} {f} _ {x} ( \vv{\rm r} ) -\varepsilon {f} _ {y} ( \vv{\rm r} ) \\ {f} _ {y} ( \vv{\rm r} ) +\varepsilon {f} _ {x} ( \vv{\rm r} ) \\ {f} _ {z} ( \vv{\rm r} ) \end{bmatrix} \end{aligned} \label{eq:alt1} \end{equation}\]

Agora, rotação do campo de vetores por meio do operador de rotação:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} \vv{f} _ {\varepsilon} ( \vv{\rm r} _ {\varepsilon} ) &= \left( \vv{1} -i\varepsilon \vv{\rm J} _ z \right) \vv{f} ( \vv{\rm r} _ {\varepsilon} ) \\ &= \left( \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} -i\varepsilon \begin{bmatrix} J _ 1 & J _ 2 & J _ 3 \\ J _ 4 & J _ 5 & J _ 6 \\ J _ 7 & J _ 8 & J _ 9 \end{bmatrix} \right) \begin{bmatrix} {f} _ {x} ( \vv{\rm r} _ {\varepsilon} ) \\ {f} _ {y} ( \vv{\rm r} _ {\varepsilon} ) \\ {f} _ {z} ( \vv{\rm r} _ {\varepsilon} ) \end{bmatrix} \\ &= \begin{bmatrix} 1-i\varepsilon J _ 1 & -i\varepsilon J _ 2 & -i\varepsilon J _ 3 \\ -i\varepsilon J _ 4 & 1-i\varepsilon J _ 5 & -i\varepsilon J _ 6 \\ -i\varepsilon J _ 7 & -i\varepsilon J _ 8 & 1-i\varepsilon J _ 9 \end{bmatrix} \begin{bmatrix} {f} _ {x} ( \vv{\rm r} _ {\varepsilon} ) \\ {f} _ {y} ( \vv{\rm r} _ {\varepsilon} ) \\ {f} _ {z} ( \vv{\rm r} _ {\varepsilon} ) \end{bmatrix} \end{aligned} \label{eq:alt2} \end{equation}\]

Expansão em série de Taylor (\(1^a\) ordem):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} {f} _ {x} ( \vv{\rm r} _ {\varepsilon} ) = {f} _ {x} ( x-\varepsilon y, y+\varepsilon x,z ) = {f} _ {x} ( \vv{\rm r} ) + \left( -\varepsilon y\frac{\partial \quad}{\partial x} +\varepsilon x\frac{\partial \quad}{\partial y} \right) {f} _ {x} ( \vv{\rm r} ) \\ {f} _ {y} ( \vv{\rm r} _ {\varepsilon} ) = {f} _ {y} ( x-\varepsilon y, y+\varepsilon x,z ) = {f} _ {y} ( \vv{\rm r} ) + \left( -\varepsilon y\frac{\partial \quad}{\partial x} +\varepsilon x\frac{\partial \quad}{\partial y} \right) {f} _ {y} ( \vv{\rm r} ) \\ {f} _ {z} ( \vv{\rm r} _ {\varepsilon} ) = {f} _ {z} ( x-\varepsilon y, y+\varepsilon x,z ) = {f} _ {z} ( \vv{\rm r} ) + \left( -\varepsilon y\frac{\partial \quad}{\partial x} +\varepsilon x\frac{\partial \quad}{\partial y} \right) {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt3} \end{equation}\]

\({ }\)

MULTIPLICAÇÃO DA MATRIZ \(\eqref{eq:alt2}\) DESPREZANDO O TERMO \(\varepsilon ^2\):

• Estrutura da \(1^a\) linha:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \begin{aligned} \left( 1-i\varepsilon J _ 1 \right) \left[ {f} _ {x} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {x} ( \vv{\rm r} ) \right] &= {f} _ {x} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {x} ( \vv{\rm r} ) -i\varepsilon J _ 1 {f} _ {x} ( \vv{\rm r} ) \\ \left( -i\varepsilon J _ 2 \right) \left[ {f} _ {y} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {y} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 2 {f} _ {y} ( \vv{\rm r} ) \\ \left( -i\varepsilon J _ 3 \right) \left[ {f} _ {z} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {z} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 3 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt4a} \end{equation}\]

\({ }\)

• Estrutura da \(2^a\) linha:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \begin{aligned} \left( -i\varepsilon J _ 4 \right) \left[ {f} _ {x} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {x} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 4 {f} _ {x} ( \vv{\rm r} ) \\ \left( 1-i\varepsilon J _ 5 \right) \left[ {f} _ {y} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {y} ( \vv{\rm r} ) \right] &= {f} _ {y} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {y} ( \vv{\rm r} ) -i\varepsilon J _ 5 {f} _ {y} ( \vv{\rm r} ) \\ \left( -i\varepsilon J _ 6 \right) \left[ {f} _ {z} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {z} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 6 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt4b} \end{equation}\]

\({ }\)

• Estrutura da \(3^a\) linha:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \begin{aligned} \left( -i\varepsilon J _ 7 \right) \left[ {f} _ {x} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {x} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 7 {f} _ {x} ( \vv{\rm r} ) \\ \left( -i\varepsilon J _ 8 \right) \left[ {f} _ {y} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {y} ( \vv{\rm r} ) \right] &= -i\varepsilon J _ 8 {f} _ {y} ( \vv{\rm r} ) \\ \left( 1-i\varepsilon J _ 9 \right) \left[ {f} _ {z} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {z} ( \vv{\rm r} ) \right] &= {f} _ {z} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {z} ( \vv{\rm r} ) -i\varepsilon J _ 9 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt4c} \end{equation}\]

\({ }\)

Igualando a \(1^a\) linha da matriz \(\eqref{eq:alt1}\) com a \(1^a\) linha da matriz \(\eqref{eq:alt2}\):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} {f} _ {x} ( \vv{\rm r} ) -\varepsilon {f} _ {y} ( \vv{\rm r} ) = {f} _ {x} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {x} ( \vv{\rm r} ) -i\varepsilon J _ 1 {f} _ {x} ( \vv{\rm r} ) -i\varepsilon J _ 2 {f} _ {y} ( \vv{\rm r} ) -i\varepsilon J _ 3 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt5a} \end{equation}\]

Igualando a \(2^a\) linha da matriz \(\eqref{eq:alt1}\) com a \(2^a\) linha da matriz \(\eqref{eq:alt2}\):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} {f} _ {y} ( \vv{\rm r} ) +\varepsilon {f} _ {x} ( \vv{\rm r} ) = -i\varepsilon J _ 4 {f} _ {x} ( \vv{\rm r} ) + {f} _ {y} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {y} ( \vv{\rm r} ) -i\varepsilon J _ 5 {f} _ {y} ( \vv{\rm r} ) -i\varepsilon J _ 6 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt5b} \end{equation}\]

Igualando a \(3^a\) linha da matriz \(\eqref{eq:alt1}\) com a \(3^a\) linha da matriz \(\eqref{eq:alt2}\):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} {f} _ {z} ( \vv{\rm r} ) = -i\varepsilon J _ 7 {f} _ {x} ( \vv{\rm r} ) -i\varepsilon J _ 8 {f} _ {y} ( \vv{\rm r} ) + {f} _ {z} ( \vv{\rm r} ) + \varepsilon \left( x\frac{\partial \quad}{\partial y}-y\frac{\partial \quad}{\partial x} \right) {f} _ {z} ( \vv{\rm r} ) -i\varepsilon J _ 9 {f} _ {z} ( \vv{\rm r} ) \end{aligned} \label{eq:alt5c} \end{equation}\]

Conclusões das equações \(\eqref{eq:alt5a}\), \(\eqref{eq:alt5b}\) e \(\eqref{eq:alt5c}\):

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \begin{aligned} J _ 1 &= -i \left( x\frac{\partial \quad}{\partial y} -y\frac{\partial \quad}{\partial x} \right) \\ J _ 2 &= -i \\ J _ 3 &= 0 \\ J _ 4 &= i \\ J _ 5 &= -i \left( x\frac{\partial \quad}{\partial y} -y\frac{\partial \quad}{\partial x} \right) \\ J _ 6 &= 0 \\ J _ 7 &= 0 \\ J _ 8 &= 0 \\ J _ 9 &= -i \left( x\frac{\partial \quad}{\partial y} -y\frac{\partial \quad}{\partial x} \right) \end{aligned} \label{eq:alt6} \end{equation}\]

\({ }\)

Logo, a componente z do momento angular de um campo de vetores é:

\[\begin{equation} \newcommand{\vv}[1]{\boldsymbol{#1}} \small \boldsymbol{\rm J} _ z = \begin{bmatrix} -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & -i & 0 \\ i & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) & 0 \\ 0 & 0 & -i\!\left(x\frac{\partial\quad}{\partial y}-y\frac{\partial\quad}{\partial x}\right) \end{bmatrix} \label{eq:alt7} \end{equation}\]

\({ }\)

9 Conclusão

A técnica de expandir uma função em uma série de Taylor é uma ferramenta matemática importante para o progresso da teoria física, em especial, para o desenvolvimento da teoria do momento angular. Por meio dessa técnica, pode-se deduzir o momento angular orbital apenas utilizando argumentos geométricos e o momento angular de um campo de vetores, ademais, nos faz entender que o operador que se associa a uma função espacial em rotação infinitesimal, é o operador do momento angular orbital, e o operador que se associa a um campo de vetores em rotação infinitesimal, é o operador do momento angular total, que inclui o operador do spin.