1 A definição de stress longitudinal

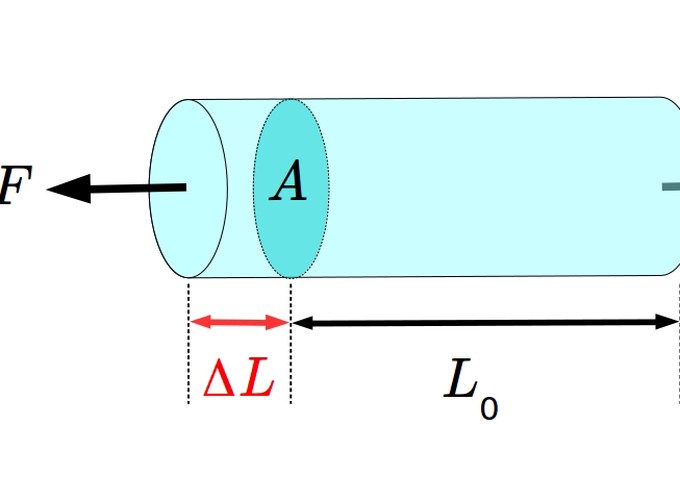
Um corpo de prova é tracionado conforme a Figura 1.1. É tracionado por forças que atuam ao longo do eixo do corpo. Uma força de intensidade \(F\) age normal à seção transversal do corpo. Seção transversal de área \(A\). Nesse ensaio de tração, a força que atua na seção transversal gera um stress no corpo de prova. Stress \(\sigma\) determinado pela relação:

\[\begin{equation} \sigma = \frac{F}{A}. \label{eq:MAX1} \end{equation}\]

O stress \(\eqref{eq:MAX1}\) é chamado de stress normal, visto que é decorrente de uma força normal. Se pensar que a força também é uma força longitudinal, pode-se dizer que \(\eqref{eq:MAX1}\) é um stress longitudinal.

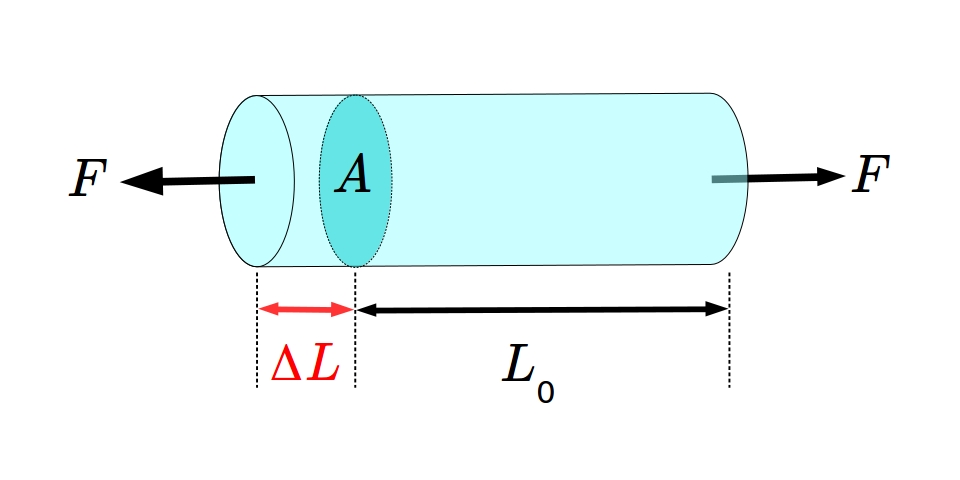
Figura 1.1: Um corpo de prova em um ensaio de tração.

2 A definição de strain longitudinal

Sem stress, o corpo de prova tem comprimento \(L_0\). O stress altera o comprimento do corpo. Modifica pelo valor \(\Delta L\). Então, o stress causa um strain no corpo de prova. Strain \(\epsilon\) determinado pela relação:

\[\begin{equation} \epsilon = \frac{\Delta L}{L _ 0}. \label{eq:MAX2} \end{equation}\]

O strain \(\eqref{eq:MAX2}\) é chamado de strain longitudinal, pelo fato de ser causado por um stress longitudinal.

3 O diagrama stress-strain

Um corpo de prova submetido a um stress longitudinal \(\sigma\) sofre um strain longitudinal \(\epsilon\). A força que atua no corpo modifica seu comprimento (modifica o valor de \(\epsilon\)), ademais, a mesma força também pode modificar a área da sua seção transversal (modificar o valor de \(\sigma\)). Uma máquina de ensaio stress-strain é projetada para fazer a medição da variação do comprimento longitudinal e da área da seção transversal, em função da força aplicada no corpo de prova. O diagrama stress-strain (\(\sigma \times \epsilon\)) é construído graficando os valores do stress \(\sigma\) (eixo y) em função dos valores do strain \(\epsilon\) (eixo x).

A região inicial do diagrama stress-strain obedece a lei de Hook, por isso é chamada de região elástica:

\[\begin{equation} F = k \Delta L. \label{eq:MAX3} \end{equation}\]

Dividindo \(\eqref{eq:MAX3}\) pela área de seção transversal, mostra-se que o stress \(\sigma\) é diretamente proporcional ao strain \(\epsilon\):

\[\begin{equation} \sigma = E \epsilon . \label{eq:MAX4} \end{equation}\]

A constante \(E\) é chamada de módulo de elasticidade ou módulo de Young. Visto que \(\epsilon\) é adimensional, \(E\) possui a mesma unidade de \(\sigma\): Pascal (Pa), sendo \(\rm 1 Pa = 1 N/m^2\).

A Figura 3.1 mostra a região elástica do diagrama stress-strain referente a uma liga de alumínio utilizada principalmente em aplicações aeroespaciais e de defesa (Pujari Srinivasa Rao 2018). O módulo de elasticidade é igual a 75 GPa (Hibbeler 2011). Como se vê, o stress \(\sigma\) = 450 MPa causa o strain \(\epsilon\) = 0,006 mm/mm: quer dizer, causa alteração de 0,006 mm, a cada 1 mm de liga sem stress, segundo a definição \(\eqref{eq:MAX2}\).

Figura 3.1: Diagrama stress-strain. Zona elástica da liga de alumínio E = 75 GPa (Hibbeler 2011).

4 A tradução dos termos para o português

Stress tem a mesma unidade da tensão mecânica: \(\rm N/m^2\). Strain relaciona-se com alteração de comprimento: o corpo de prova é tracionado ou comprimido, de maneira geral, é deformado. Por isso, Conceitos de Stress e Strain Longitudinais é traduzido como:

Conceitos de Tensão e Deformação Longitudinais.