1 Introdução

A decomposição do movimento vibratório em componentes dinamicamente independentes é chamada de decomposição de modo normal.

O “complicado” é resultado da superposição de “descomplicados.”

A vibração molecular é resultado da superposição de modos normais, ou, se quiser, sobreposição de vibrações nítidas, independentes e desacopladas.

O modo normal é a maneira mais organizada de movimento vibracional. Vamos exemplificar com a molécula de água. A estar a água em um modo normal específico, cada átomo (hidrogênio, hidrogênio e oxigênio) atinge seu deslocamento máximo ao mesmo tempo e passa por sua posição de equilíbrio ao mesmo tempo. Isso quer dizer que vibram com a mesma frequência \((\nu)\). Considere rotular os átomos por \(1,2,3\). Em um modo normal:

\[\begin{equation} \nu ^{(1)} = \nu ^{(2)} = \nu ^{(3)} . \tag{1.1} \end{equation}\]

Porém, a situação (1.1) não significa que os átomos vão sempre vibrar com a mesma amplitude \((A)\). A amplitude pode alterar.

A Fig. 1.1 foi construída para exclarecer a igualdade de frequência e a possível desigualdade de amplitude.

Uma molécula diatômica, na representação de massa reduzida, vibra no modo normal de frequência \(\nu\).

No caso (a), a amplitude de vibração é \(A_a\). No (b), \(A_b\). E no (c), \(A_c\).

No tempo \(t_{I}\), atinge-se a amplitude máxima. No \(t_{II}\), passa-se pela posição de equilíbrio. E no \(t_{III}\), atinge-se novamente a amplitude máxima.

Pela construção da figura:

\[\begin{equation} \begin{aligned} A _ b &= 2 A _ a ,\\ A _ c &= 3 A _ a . \end{aligned} \tag{1.2} \end{equation}\]

Se as frequências nos três casos são iguais, então, os períodos nos três casos também são iguais. De fato, o período para se realizar uma oscilação completa é sempre \(\mathtt{T} = 1/\nu\). Portanto, as velocidades das oscilações são diferentes. A utilizar os deslocamentos de 1 ciclo, pode-se estimar a velocidade média em cada caso:

\[\begin{equation} \begin{aligned} v _ a &= \frac{4A _ a}{T}, \\ v _ b &= \frac{4A _ b}{T} = 2v _ a, \\ v _ c &= \frac{4A _ c}{T} = 3v _ a. \end{aligned} \tag{1.3} \end{equation}\]

Há relação: o caso de maior amplitude – (c) – é o caso de maior velocidade \((3v _ a)\), e o caso de menor amplitude – (a) – é o caso de menor velocidade \((v _ a)\). Em outras palavras, o caso de maior amplitude é o de maior energia, e o caso de menor amplitude é o de menor energia. Podemos resumir assim:

Em um modo de frequência única, o caso de maior energia é o de maior amplitude de vibração.

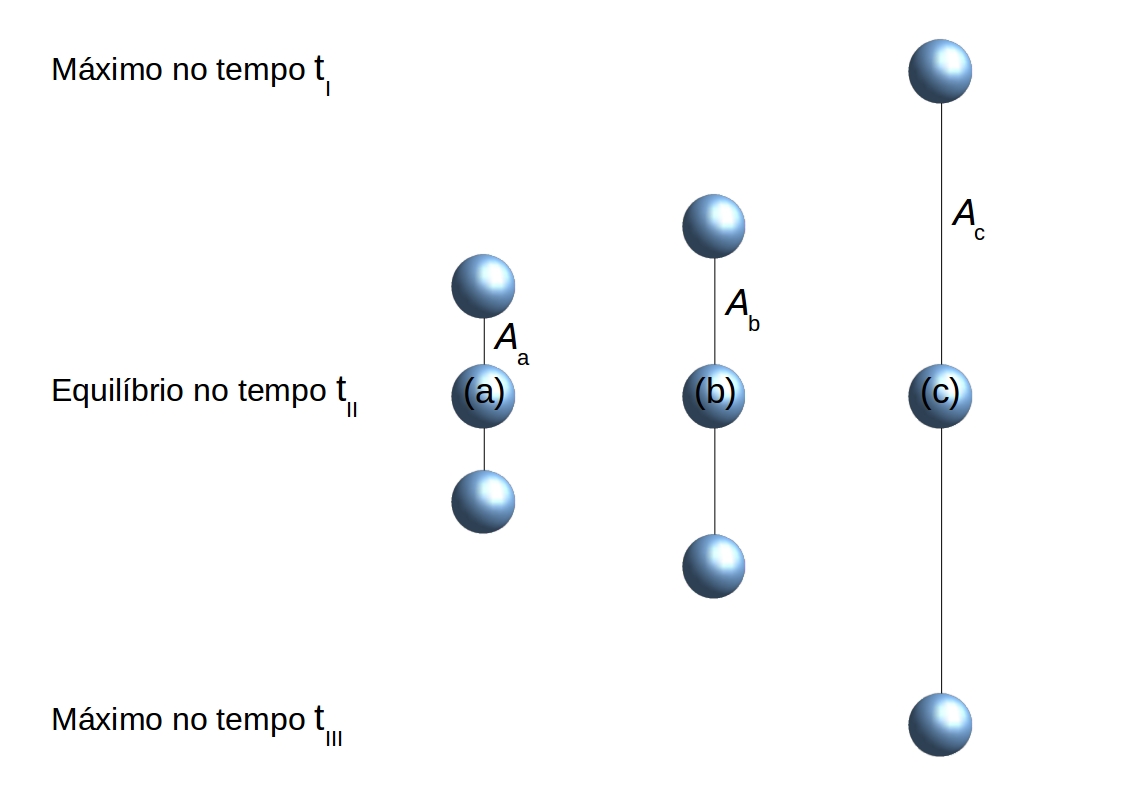
Figura 1.1: Molécula diatômica na representação de massa reduzida. Nas situações (a), (b) e (c), a molécula vibra com a mesma frequência, porém, com amplitudes diferentes.

A energia vibracional, do ponto de vista da mecânica quântica, é discutida no artigo: Energia Vibracional e Rotacional de Molécula Diatômica. No modelo harmônico, a energia vibracional é:

\[\begin{equation} G _ {\nu} = \left( \nu + \tfrac{1}{2} \right) \overline{\nu} . \tag{1.4} \end{equation}\]

Nessa fórmula, \(\nu\) é o número quântico vibracional \((0,1,2,3...)\); e \(\overline{\nu}\) é a frequência de vibração em unidade \(\rm {cm}^{-1}\) (número de onda).

Uma molécula, no estado fundamental do modo \(\overline{\nu}_{\star}\), vibra com a energia \(G _ 0 = \tfrac{1}{2} \overline{\nu}_{\star}\).

A mesma molécula, no primeiro estado excitado do mesmo modo, vibra com a \(G _ 1 = \tfrac{3}{2} \overline{\nu}_{\star}\).

A mesma molécula, agora no segundo estado excitado do mesmo modo, vibra com a \(G _ 2 = \tfrac{5}{2} \overline{\nu}_{\star}\).

E assim por diante.

A lembrar que, em um modo normal, o caso de maior energia é o caso de maior amplitude, conclui-se que a molécula no estado fundamental possui a menor amplitude de vibração, e a amplitude aumenta com o aumento do número quântico.

2 Modos normais de vibração da água

Uma molécula tridimensional formada por \(N\) átomos possui \(M\) modos normais de vibração:

\[\begin{equation} M = 3N - 6. \tag{2.1} \end{equation}\]

Segundo a equação (2.1), a molécula de água \((N=3)\) possui 3 modos normais de vibração. Neste trabalho, as frequências dos modos foram determinadas por meio de cálculo ab initio, utilizando o software GAMESS [ver link do portal nas referências]:

\[\begin{equation} \begin{aligned} \overline{\nu} _ {\rm 1} &= 1580\ {\rm cm^{-1}}, \\ \overline{\nu} _ {\rm 2} &= 3602\ {\rm cm^{-1}}, \\ \overline{\nu} _ {\rm 3} &= 3826\ {\rm cm^{-1}}. \end{aligned} \tag{2.2} \end{equation}\]

A Fig. 2.1 apresenta os modos normais de vibração da água. Replicando a equação (1.4), a energia de cada modo é:

\[\begin{equation} \begin{aligned} G _ {\nu _ 1} = \left(\nu _ {1} + \tfrac{1}{2} \right) \overline{\nu} _ {1} ,\\ G _ {\nu _ 2} = \left(\nu _ {2} + \tfrac{1}{2} \right) \overline{\nu} _ {2} ,\\ G _ {\nu _ 3} = \left(\nu _ {3} + \tfrac{1}{2} \right) \overline{\nu} _ {3} . \end{aligned} \tag{2.3} \end{equation}\]

Os primeiros valores das energias (2.3) são listados na Tabela 2.1.

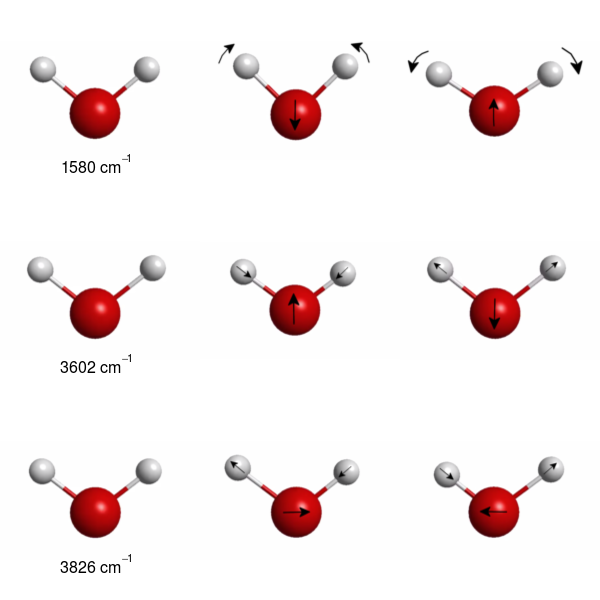
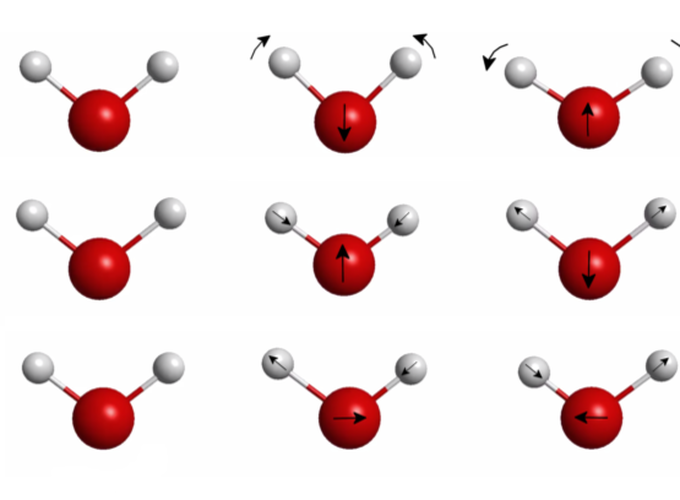
Figura 2.1: Três modos normais de vibração da água.

3 Modos combinados de vibração da água

Além da vibração normal, a molécula de água também pode ser encontrada em uma vibração combinada, oscilando de acordo com uma superposição de modos normais. Na vibração combinada, a energia da molécula é igual à soma das energias dos modos normais:

\[\begin{equation} W _ {(\nu _ 1, \nu _ 2, \nu _ 3)} = \left(\nu _ {1} + \tfrac{1}{2} \right) \overline{\nu} _ {1} + \left(\nu _ {2} + \tfrac{1}{2} \right) \overline{\nu} _ {2} + \left(\nu _ {3} + \tfrac{1}{2} \right) \overline{\nu} _ {3} . \tag{3.1} \end{equation}\]

As frequências normais de vibração da água foram impressas no local (2.2).

Combinando os números quânticos \((\nu_1,\nu_2,\nu_3)\), pode-se ordenar as energias vibracionais da água. Por exemplo, a menor energia ocorre para \((\nu_1,\nu_2,\nu_3) = (0,0,0)\), e tem o valor \(W_{(0,0,0)} = 4504\ {\rm cm^{-1}}\); a Tabela 3.1 apresenta outros valores.

4 Conclusão

A vibração da água pode ocorrer em modo normal, organizado, no qual os átomos passam pela posição de equilíbrio ao mesmo tempo e vibram na mesma frequência. De acordo com a igualdade de frequência e desigualdade de amplitude, a molécula em modo de frequência única pode modificar sua energia (amplitude) sem alterar sua frequência vibracional. A vibração da água também pode ocorrer em modo combinado, no qual frequências são sobrepostas de acordo com superposição de modos normais.