- 1 Introdução
- 2 A energia vibracional
- 3 A energia rotacional
- 4 A energia de excitação adiabática
- 5 Considerações finais
- Referências
1 Introdução
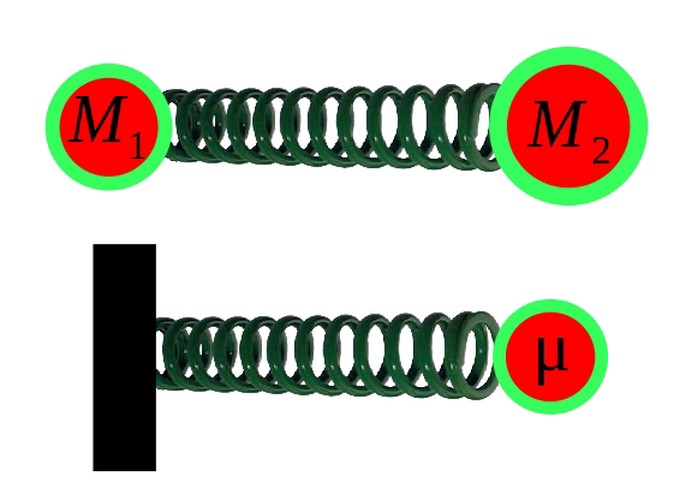
A molécula diatômica é uma molécula simples. O sistema vibracional-rotacional de 2-massas \((M_1, M_2)\) é equivalente ao sistema vibracional-rotacional de 1-massa reduzida \((\mu)\). Por isso, as soluções do oscilador quântico e do rotor rígido quântico se tornam apropriadas para descrever a vibração e a rotação da molécula diatômica.
Quando se estuda o oscilador e o rotor rígido, pode ser que grande parte da análise seja dedicada para se encontrar os autovalores e as autofunções das equações de Schrödinger e, talvez, se gaste pouco tempo para se aplicar os resultados encontrados. Entretanto, pode-se equilibrar a pesquisa. Há na literatura dados experimentais sobre a vibração e rotação de moléculas diatômicas. Cito, como exemplo, os dados publicados por (Sala 2008), (W Kiefer 1972) e (Richard F Barrow 1973). Verificar como esses dados são explicados pelos modelos vibracional harmônico, vibracional anarmônico e rotacional rígido, é o objetivo deste artigo.
2 A energia vibracional
2.1 A vibração nuclear
Uma molécula diatômica, como o nome diz, é formada por dois átomos. Os átomos se mantém ligados por causa de um jogo de forças que envolve os núcleos e os elétrons que se distribuem ao redor dos núcleos atômicos. Esse jogo de forças é ilustrado na Figura 2.1.
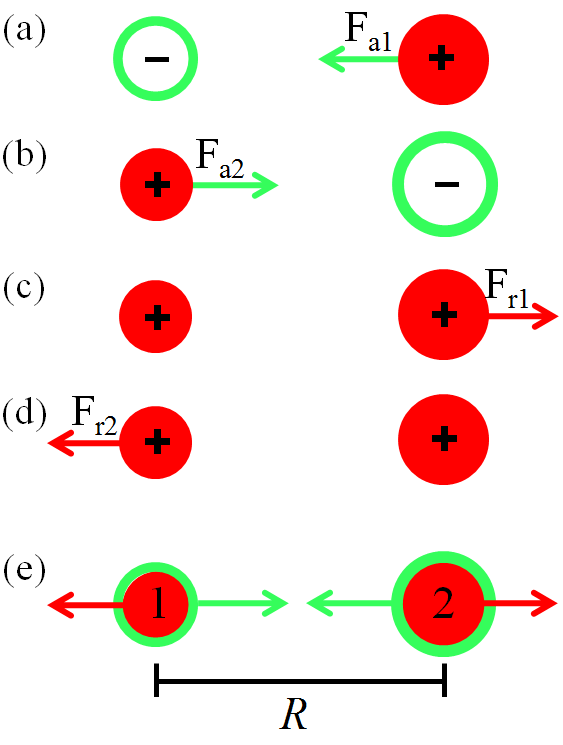
Figura 2.1: Forças em uma molécula diatômica.
Como dissemos, a Figura 2.1 ilustra o jogo de forças que ocorre em uma molécula diatômica. São apresentadas 4 forças. Na parte (a), a distribuição dos elétrons ao redor do núcleo 1, gera a força atrativa \(F_{a1}\) no núcleo 2. Na parte (b), a distribuição dos elétrons ao redor do núcleo 2, gera a força atrativa \(F_{a2}\) no núcleo 1. Na parte (c), a distribuição dos prótons do núcleo 1, gera a força repulsiva \(F_{r1}\) no núcleo 2. Na parte (d), a distribuição dos prótons do núcleo 2, gera a força repulsiva \(F_{r2}\) no núcleo 1. Então, simultaneamente, temos o jogo de forças (e). Nesse jogo, os núcleos atuam para afastar um átomo do outro, para ocorrer certo aumento da distância internuclear, que chamaremos de \(R\). Já os elétrons agem ao contrário, atuam para aproximar um átomo do outro. Então, é dos elétrons o papel de manter os núcleos atômicos coesos para se formar a molécula diatômica.
Visto que os movimentos de afastamento e aproximação são periódicos, os núcleos vibram em torno de uma distância de equilíbrio, que chamaremos de \(R_e\). Eles se aproximam até uma distância mínima, que chamaremos de \(R_-\) e, depois, se afastam até certa distância máxima, que chamaremos \(R_+\). A vibração nuclear \(\left( R_- \iff R_+ \right)\), em torno do equilíbrio \(R_e\), é apresentada na Figura 2.2.
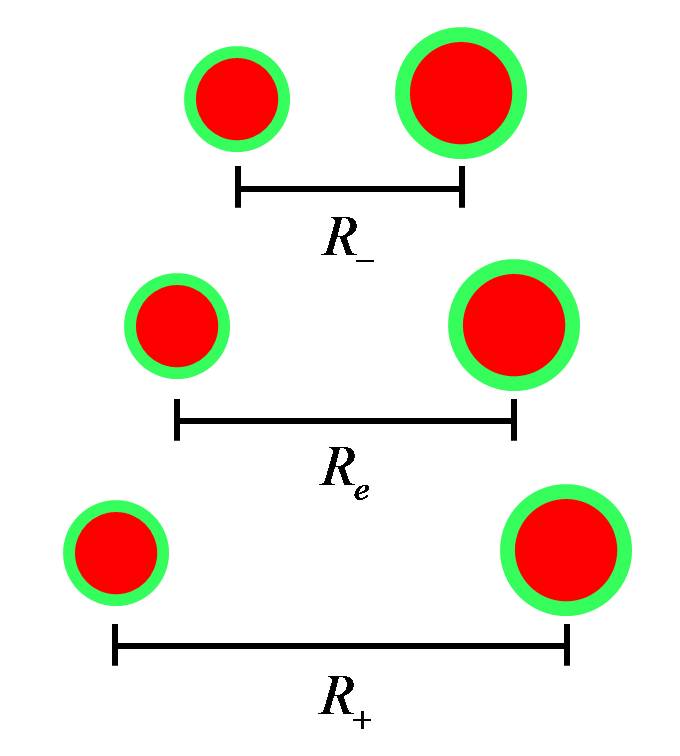
Figura 2.2: Vibração nuclear em torno da distância de equilíbrio.
Seguindo a nomenclatura da Figura 2.2, se \(\left( R_e - R_- \right) = \left( R_+ - R_e \right)\), a vibração é dita harmônica, mas, caso ocorra, \(\left( R_e - R_- \right) < \left( R_+ - R_e \right)\), a vibração é sem harmonia, ou, como se diz, a vibração é anarmônica. Por exemplo, a vibração com \(R_e=3\), \(R_-=2\) e \(R_+=4\), é do tipo harmônica, mas se o afastamento máximo fosse \(R_+=5\), a vibração seria do tipo anarmônica (valores arbitrários).
2.2 Uma energia potencial rústica
Dá-se o nome de energia potencial eletrostática, que chamaremos de \(V\), a energia associada à distância entre cargas elétricas. Se as cargas forem pontuais, do tipo, \(Q_1\) e \(Q_2\), e se a distância entre elas for \(R\), a energia potencial eletrostática tem a seguinte relação de dependência:
\[\begin{equation} V \propto \frac{Q_1 Q_2}{R}. \label{eq:MAX1} \end{equation}\]
Uma maneira simplória de escrever a energia total associada à separação das cargas da molécula diatômica, é considerar a energia potencial de repulsão (núcleo-núcleo) inversamente proporcional à distância internuclear,
\[\begin{equation} V _ {\rm N\mbox{-}N} \propto \frac{1}{R}, \label{eq:MAX2} \end{equation}\]
e a energia potencial de atração (núcleo-elétron), diretamente proporcional à distância internuclear,
\[\begin{equation} V _ {\rm N\mbox{-}e} \propto R. \label{eq:MAX3} \end{equation}\]
Então, segundo \(\eqref{eq:MAX2}\) e \(\eqref{eq:MAX3}\), a energia potencial total de certa distribuição de elétrons ao redor de núcleos de uma molécula diatômica tem a seguinte relação de dependência:
\[\begin{equation} V _ {\rm T} \propto \frac{1}{R} + R. \label{eq:MAX4} \end{equation}\]
A Figura 2.3 mostra o comportamento da relação \(\eqref{eq:MAX4}\). Nessa Figura, a distância internuclear começa próximo de zero e aumenta até 10 (valores arbitrários). Observamos que a energia potencial total apresenta um mínimo, de valor \(V(R_e)\), e que, ao redor da distância de equilíbrio \(R_e\), a curva não é simétrica. Uma curva simétrica seria do tipo parabólica, \(V(R) \propto R^2\), e, nesse caso, a vibração em torno do equilíbrio seria harmônica. Visto que a curva \(\eqref{eq:MAX4}\) não é simétrica, a vibração em torno do equilíbrio é anarmônica, sendo a separação máxima dos núcleos maior que a separação mínima, ou seja, \(R_+ > R_-\). Em relação à distância de equilíbrio, o lado esquerdo da curva, região \(R < R_e\), é predominantemente influenciado pela repulsão (núcleo-núcleo), enquanto que o lado direito, região \(R > R_e\), é influenciado pela pela atração (elétron-núcleo): indicado pelas curvas de apoio pontilhadas, construídas pelas equações \(\eqref{eq:MAX2}\) e \(\eqref{eq:MAX3}\). Portanto, a Figura 2.3 incorpora o aspecto vibracional de uma molécula diatômica.
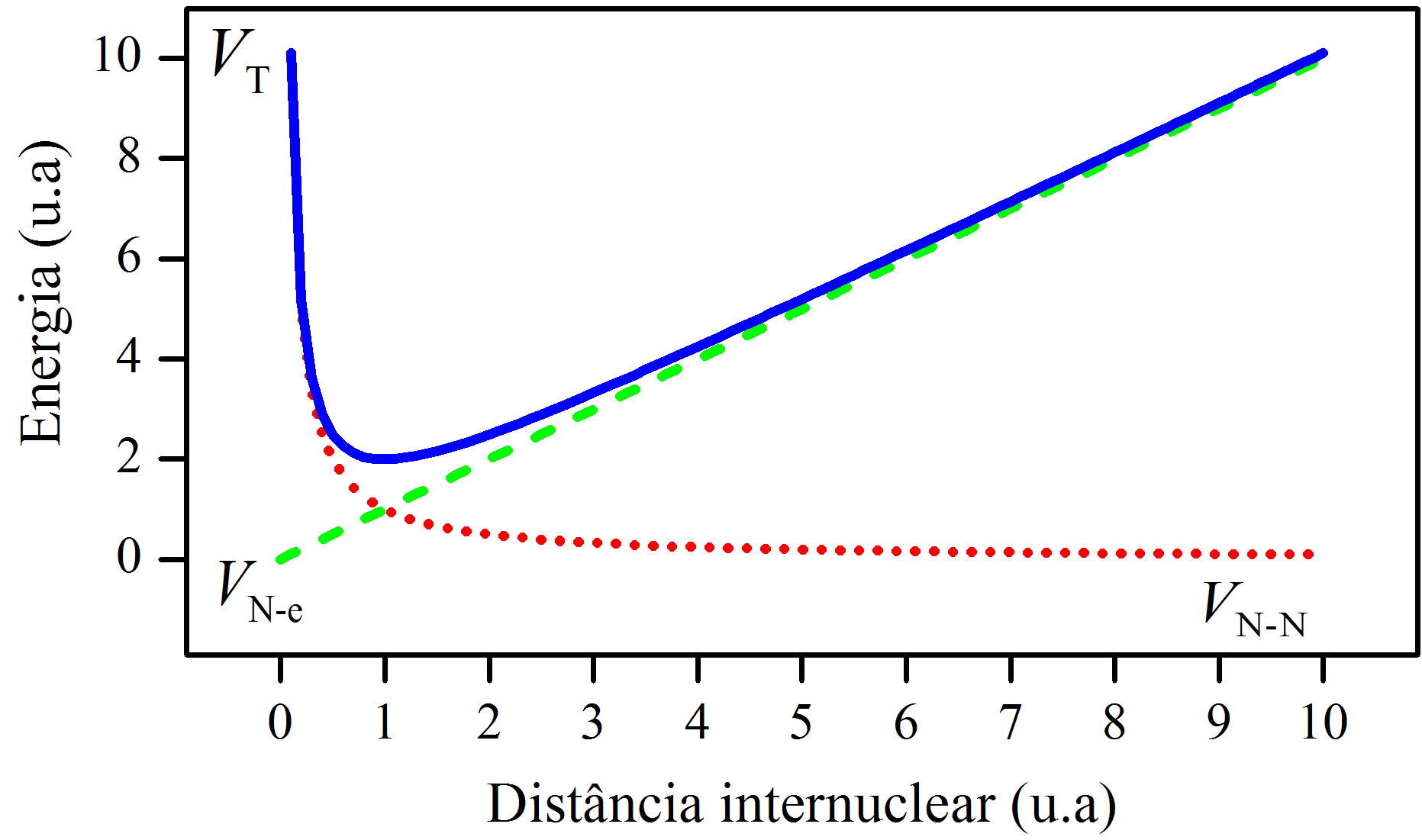
Figura 2.3: Perfil da energia potencial de uma molécula diatômica.
2.3 A energia potencial elástica
O caráter vibracional da molécula diatômica é decorrente de forças repulsivas e atrativas presentes na molécula, conforme ilustrado na Figura 2.1. Um modelo para descrever a vibração molecular incorpora em uma mola fictícia, de constante elástica \(k\), o papel das forças de repulsão (núcleo-núcleo) e de atração (elétron-núcleo). Diz-se, então, que os átomos estão ligados por mola, conforme ilustrado na Figura 2.4. Nesse modelo, a força de interação entre os átomos é a força elástica, e a energia potencial vinculada à força elástica, é a energia potencial elástica:
\[\begin{equation} V _ {\rm e} = \frac{1}{2}k \left(R - R_e \right)^2. \label{eq:MAX5} \end{equation}\]
A expressão \(\eqref{eq:MAX5}\) é a primeira aproximação da energia potencial ao redor da distância de equilíbrio do poço da Figura 2.3: região caracterizada pelos núcleos não se afastarem muito da distância de equilíbrio, e, por isso, com a possibilidade de ser considerada harmônica.
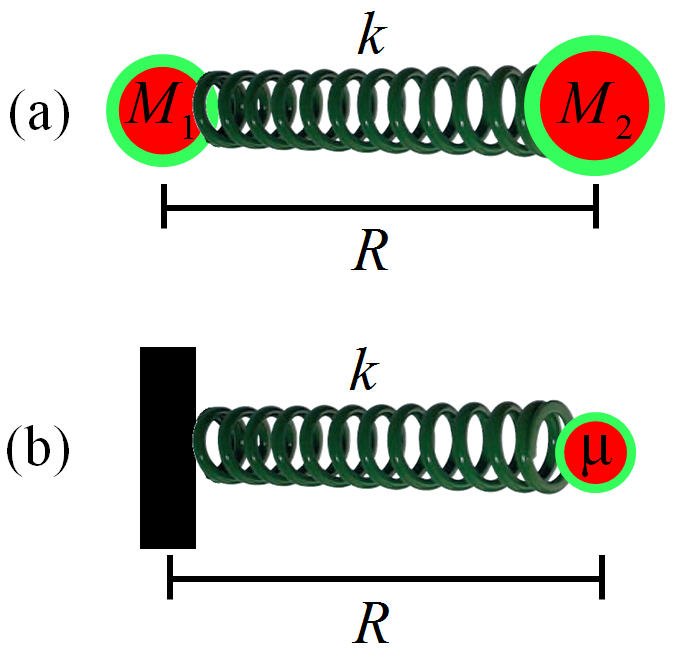
Figura 2.4: Átomos ligados por mola: a distância \(R\) entre as massas \(M_1\) e \(M_2\) equivale à posição \(R\) da massa \(\mu\).
A molécula diatômica ligada por mola como representada na Figura 2.4, parte (a), pode também ser modelada pelo arranjo equivalente que aparece na mesma Figura, parte (b). Para isso, há necessidade de se introduzir o conceito de massa reduzida:
\[\begin{equation} \mu = \frac{M_1 M_2}{M_1 + M_2}, \label{eq:MAX6} \end{equation}\]
onde \(M_1\) e \(M_2\) são as massas dos núcleos 1 e 2, respectivamente. Nesse novo modelo, a vibração molecular passa a ser descrita pela vibração de uma única partícula de massa \(\mu\) presa a uma mola de constante elástica \(k\).
2.4 O modelo vibracional harmônico
Além da energia associada à distância, potencial \(V\), a vibração molecular também manifesta energia associada à velocidade, cinética \(T\), sendo a energia total \(E\), a soma dessas duas parcelas:
\[\begin{equation} E = T(R) + V(R). \label{eq:MAX7} \end{equation}\]
Considere a representação por massa reduzida, Figura 2.4, parte (b). Ao vibrar, a massa reduzida representa a oscilação entre certa distância internuclear mínima \(R_-\) e máxima \(R_+\). Considere também que, ao estar em \(R\), o momento da massa reduzida seja \(p(R)\). Então, aproximando a função energia potencial pela expressão harmônica, a equação \(\eqref{eq:MAX7}\) fica:
\[\begin{equation} E = \frac{\left[p(R)\right]^2}{2\mu} + \frac{1}{2}k \left(R - R_e \right)^2. \label{eq:MAX8} \end{equation}\]
Ao atingir \(R_-\), a massa reduzida representa a inversão do movimento nuclear, então, o momento é nulo. Substituindo \(p(R_-)=0\) em \(\eqref{eq:MAX8}\), a energia total deixa de depender do termo cinético:
\[\begin{equation} E = \frac{1}{2}k \left(R _ {-} - R _ e \right)^2. \label{eq:MAX9} \end{equation}\]
Num caso extremo, imaginando ausência de vibração, supondo \(R_-=R_e\) em \(\eqref{eq:MAX9}\), a energia total atinge o mínimo valor possível:
\[\begin{equation} E _ {\rm mín} = 0. \label{eq:MAX10} \end{equation}\]
Em um outro caso extremo, agora imaginando os núcleos se tocando, supondo \(R_-=0\) em \(\eqref{eq:MAX9}\), a energia total atinge o máximo valor possível:
\[\begin{equation} E _ {\rm máx} = \frac{1}{2}k R_e^2. \label{eq:MAX11} \end{equation}\]
Portanto, alterando continuamente o valor da distância mínima entre núcleos, de \(R_-=R_e\) até \(R_-=0\), a energia total assume um contínuo de valores dentro do intervalo \(E_{\rm mín} < E < E_{\rm máx}\), conforme resultados \(\eqref{eq:MAX10}\) e \(\eqref{eq:MAX11}\) \(-\) esta é a visão clássica do problema.
O tratamento quântico da vibração molecular, consiste em resolver a equação de Schrödinger \(\hat H \Psi=E\Psi\). O operador da energia total vibracional, \(\hat H\), é construído utilizando a expressão de certa energia total clássica: no caso do modelo vibracional harmônico, de massa reduzida \(\mu\), utiliza-se a expressão \(\eqref{eq:MAX8}\). Os procedimentos matemáticos são detalhados em livros de mecânica quântica (Phillips 2003) (Griffiths 2016). Aqui vamos reproduzir o resultado final da energia total vibracional, considerando o modelo vibracional harmônico:
\[\begin{equation} E _ \nu = (\nu + 0,\!5)\, \hbar \omega _ {\rm e}, \label{eq:MAX12} \end{equation}\]
onde \(\nu = 0, 1, 2, 3, ...\) é o número quântico vibracional, \(\hbar\) é a constante de Planck reduzida, de valor \(1,\!055 \times 10^{-34}\ {\rm Js}\), e \(\omega_{\rm e}\) é a frequência angular harmônica:
\[\begin{equation} \omega _ {\rm e} = \sqrt{\frac{k}{\mu}}. \label{eq:MAX13} \end{equation}\]
Nota 1: a frequência angular harmônica \(\omega_{\rm e}\) se relaciona com a frequência harmônica \(\nu_{\rm e}\), sendo \(\omega_{\rm e}=2\pi \nu_{\rm e}\).
Nota 2: o subíndice “\({\rm e}\)” faz alusão à palavra \({\rm e}\)lástica, de força \({\rm e}\)lástica.
Diferente do resultado clássico, onde os valores da energia total formam uma sequência ordenada ininterrupta (contínua), no resultado quântico, a energia total é quantizada, e forma o conjunto discreto:
\[\begin{align} E _ 0 &= 0,\!5\, \hbar \omega _ {\rm e}, \label{eq:MAX14} \\ E _ 1 &= 1,\!5\, \hbar \omega _ {\rm e}, \notag \\ E _ 2 &= 2,\!5\, \hbar \omega _ {\rm e}, \notag \\ &\vdots \\ E _ {\nu \, {\rm , máx}} &< E _ {\rm máx}\ \ {\rm [clássico,\ \eqref{eq:MAX11} ]}. \notag \end{align}\]
Outro destaque do resultado quântico é que a energia total mínima nunca é zero: seu valor é \(E_0\) \(\eqref{eq:MAX14}\); compare com a interpretação clássica \(\eqref{eq:MAX10}\). Isso quer dizer que sempre há um modo de vibração, sendo a ausência de vibração \((R_-=R_e)\) irrealizável.
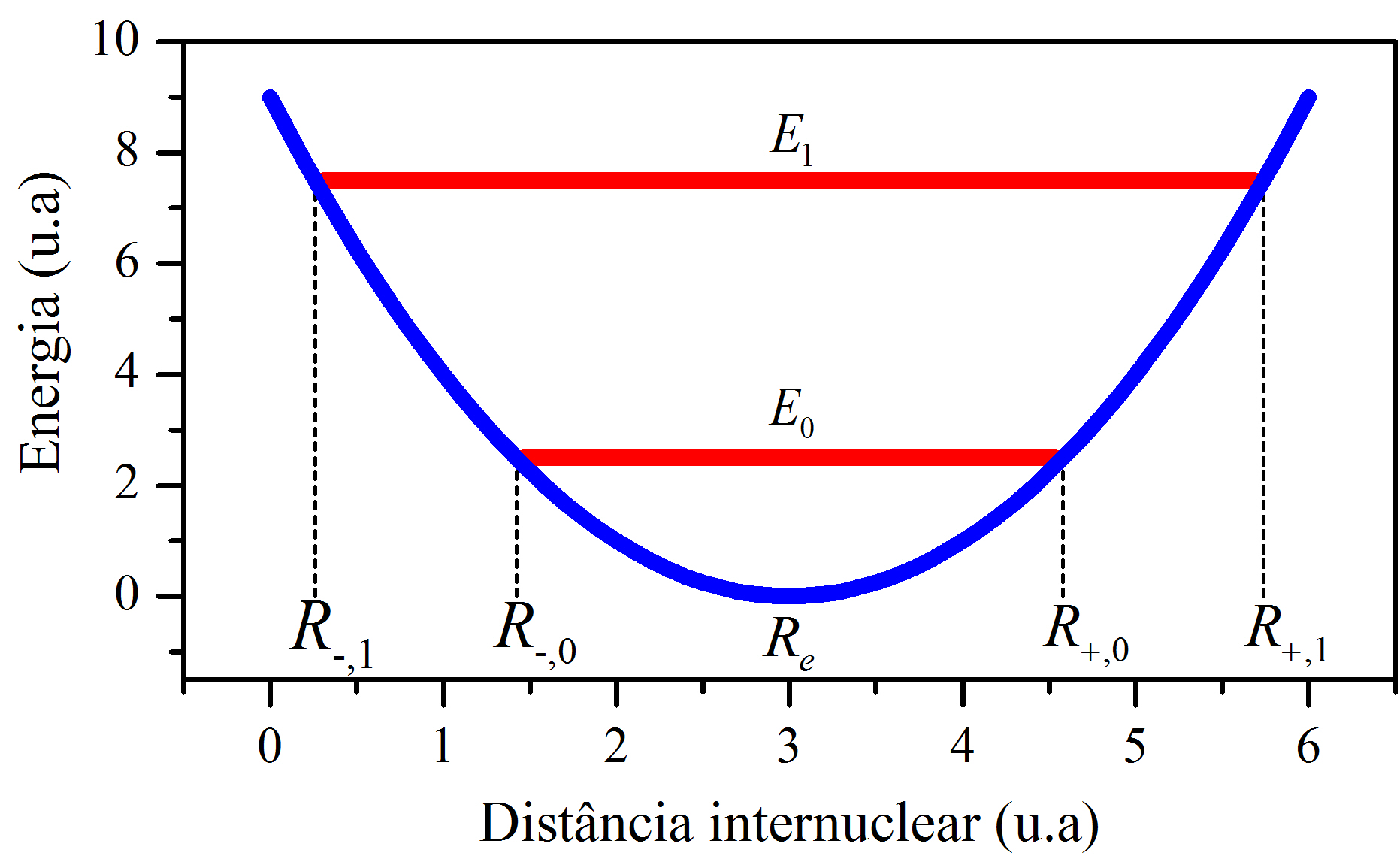
Figura 2.5: Um poço de energia potencial elástica (parábola) assinalado com certos níveis de energia (retas).
A Figura 2.5 mostra um poço de energia potencial elástica assinalado com dois níveis de energia total. Como se vê, como consequência da quantização da energia total \(\eqref{eq:MAX12}\), a distância mínima e máxima entre núcleos passa a ser quantizada, ou seja, os valores de \(R_-\) e \(R_+\) deixam de ser contínuos. Podemos explicitar isso, igualando \(\eqref{eq:MAX12}\) com \(\eqref{eq:MAX9}\)
\[\begin{equation} (\nu + 0,5)\, \hbar \omega _ {\rm e} = \frac{1}{2}k \left(R _ {-} - R _ e \right)^2. \label{eq:MAX15} \end{equation}\]
Visto que \(k=\mu \omega _ {\rm e}^2\) \(\eqref{eq:MAX13}\), a equação \(\eqref{eq:MAX15}\) pode ser reescrita como:
\[\begin{equation} \left( R _ {-} - R _ e \right)^2 = \frac{2\hbar(\nu + 0,\!5)}{\mu \omega _ {\rm e}}. \label{eq:MAX16} \end{equation}\]
A resolução da equação \(\eqref{eq:MAX16}\) implica em:
\[\begin{equation} R _ {-} - R _ e = \pm \sqrt{ \frac{2\hbar(\nu + 0,\!5)}{\mu \omega _ {\rm e}} }. \label{eq:MAX17} \end{equation}\]
Nota: o resultado \((+)\) coincide com o valor da distância internuclear máxima \(R_+\).
O resultado \(\eqref{eq:MAX17}\) prova que a distância mínima entre núcleos depende do número quântico vibracional \(\nu\):
\[\begin{equation} R _ {-,\nu} = R_e - \sqrt{ \frac{2\hbar(\nu + 0,\!5)}{\mu \omega _ {\rm e}} }. \label{eq:MAX18} \end{equation}\]
Analogamente, a distância máxima entre núcleos também é quantizada:
\[\begin{equation} R _ {+,\nu} = R_e + \sqrt{ \frac{2\hbar(\nu + 0,\!5)}{\mu \omega _ {\rm e}} }. \label{eq:MAX19} \end{equation}\]
A Tablela 2.1 sintetiza os conceitos vibracionais do modelo vibracional harmônico. Analisando a tabela, tente responder as questões logo abaixo.
| Número quântico | Frequência de vibração | Energia total | Distância mínima entre núcleos | Distância máxima entre núcleos |
|---|---|---|---|---|
| \(\nu = 0\) | \(\omega_{\rm e}\) | \(E_0 = 0,\!5 \hbar \omega_{\rm e}\) | \(R_{-,0} = R_e - \sqrt{\frac{2 \hbar (0,5)}{\mu \omega_{\rm e}}}\) | \(R_{+,0} = R_e + \sqrt{\frac{2 \hbar (0,5)}{\mu \omega_{\rm e}}}\) |
| \(\nu = 1\) | \(\omega_{\rm e}\) | \(E_1 = 1,\!5 \hbar \omega_{\rm e}\) | \(R_{-,1} = R_e - \sqrt{\frac{2 \hbar (1,5)}{\mu \omega_{\rm e}}}\) | \(R_{+,1} = R_e + \sqrt{\frac{2 \hbar (1,5)}{\mu \omega_{\rm e}}}\) |
| \(\nu = 2\) | \(\omega_{\rm e}\) | \(E_2 = 2,\!5 \hbar \omega_{\rm e}\) | \(R_{-,2} = R_e - \sqrt{\frac{2 \hbar (2,5)}{\mu \omega_{\rm e}}}\) | \(R_{+,2} = R_e + \sqrt{\frac{2 \hbar (2,5)}{\mu \omega_{\rm e}}}\) |
QUESTÕES:
Ao ganhar energia, a molécula vibra com frequência maior?
Ao ganhar energia, a molécula vibra com amplitude maior?
Ao ganhar energia, a distância mínima entre núcleos diminui?
Ao ganhar energia, a distância máxima entre núcleos aumenta?
2.5 A unidade da energia
Considere a energia escrita como o produto da constante de Planck \(h\) pela frequência \(\nu\). No Sitema Internacional:
\[\begin{align} E = h\nu & \ \ \Longleftarrow \ \ {\rm J}, \label{eq:MAX20}\\ h & \ \ \Longleftarrow \ \ {\rm Js}, \notag\\ \nu & \ \ \Longleftarrow \ \ {\rm s^{-1}}. \notag \end{align}\]
A energia \(\eqref{eq:MAX20}\) pode ser adaptada para sua unidade ser o \({\rm cm^{-1}}\). Para isso, usa-se o fato da velocidade da luz ser o produto do comprimento de onda \(\lambda\) pela frequência \(\nu\):
\[\begin{align} c = \lambda\nu & \ \ \Longleftarrow \ \ {\rm cm/s}, \label{eq:MAX21}\\ \lambda & \ \ \Longleftarrow \ \ {\rm cm}. \notag \end{align}\]
Substituindo \(\eqref{eq:MAX21}\) em \(\eqref{eq:MAX20}\):
\[\begin{equation} E = \frac{hc}{\lambda}. \label{eq:MAX22} \end{equation}\]
Agora, reescrevendo \(\eqref{eq:MAX22}\) e definindo novas grandezas:
\[\begin{align} \frac{E}{hc} &= \frac{1}{\lambda}, \label{eq:MAX23}\\ \notag\\ G &\equiv \frac{E}{hc}, \label{eq:MAX23b}\\ \notag\\ \overline{\nu} &\equiv \frac{1}{\lambda}, \label{eq:MAX23c}\\ \notag\\ G &= \overline{\nu}. \label{eq:MAX24} \end{align}\]
Portanto, \(\eqref{eq:MAX24}\) é \(\eqref{eq:MAX20}\), mas na unidade \({\rm cm^{-1}}\).
\({ }\)
\(\blacklozenge\ \) A energia total de um oscilador harmônico quântico é [ seção 2.4 ]:
\[\begin{equation} E _ \nu = (\nu + 0,\!5)\, h\nu _ {\rm e} \ \ \Longleftarrow \ \ {\rm J}, \label{eq:MAX25} \end{equation}\]
onde \(\nu\) é o número quântico vibracional, e \(\nu_{\rm e}\) é a frequência harmônica: frequência temporal, ou, simplesmente, frequência \(\left({\rm s^{-1}}\right)\).
Na nova unidade de energia, \(\eqref{eq:MAX25}\) muda para:
\[\begin{equation} G _ \nu = (\nu + 0,\!5)\, \overline{\nu} _ {\rm e} \ \ \Longleftarrow \ \ {\rm cm^{-1}}, \label{eq:MAX26} \end{equation}\]
onde \(\overline{\nu}_{\rm e}\) é o número de onda: frequência espacial, ou, simplesmente, frequência \(\left({\rm cm^{-1}}\right)\).
Ademais, utilizando \(\eqref{eq:MAX23c}\) em \(\eqref{eq:MAX21}\), vê-se que a velocidade da luz “amarra” a frequência temporal com a espacial:
\[\begin{equation} c = \frac{{\nu} _ {\rm e}} {\overline{\nu} _ {\rm e}}. \label{eq:MAX26b} \end{equation}\]
2.6 O modelo vibracional anarmônico
No modelo vibracional harmônico [ seção 2.4 ], aproxima-se o poço da função energia potencial por uma função parabólica, de segundo grau. Em outras palavras, aproxima-se certa vibração anarmônica por uma vibração harmônica. Nosso objetivo, agora, é melhorar a aproximação, indroduzindo um termo de terceira ordem. Para isso, usamos a técnica de escrever a função energia potencial em uma série de Taylor em torno da separação de equilíbrio \(R_e\):
\[\begin{equation} V(R) \ = \ V(R_e) \ + \ \left[ \frac{{\rm d}V}{{\rm d}R} \right] _ {R_e} (R-R_e) \ + \ \frac{1}{2!} \left[ \frac{{\rm d}^2V}{{\rm d}R^2} \right] _ {R_e} (R-R_e)^2 \ + \ \frac{1}{3!} \left[ \frac{{\rm d}^3V}{{\rm d}R^3} \right] _ {R_e} (R-R_e)^3 \ + \ \cdots \label{eq:MAX27} \end{equation}\]
Quando ajustamos \(V(R_e)=0\), e truncamos a função de energia potencial \(\eqref{eq:MAX27}\) no termo de segunda ordem, a energia total do oscilador quântico é a já conhecida expressão [ seção 2.5 ]:
\[\begin{equation} G _ \nu = \overline{\nu} _ {\rm e} (\nu + 0,\!5). \label{eq:MAX28} \end{equation}\]
Todavia, quando truncamos \(\eqref{eq:MAX27}\) no termo de terceira ordem, aparece um termo adicional na expressão da energia total:
\[\begin{equation} G _ \nu = \overline{\nu} _ {\rm e} (\nu + 0,\!5) - \overline{\nu} _ {\rm e} \chi _ {\rm e} (\nu + 0,\!5)^2, \label{eq:MAX29} \end{equation}\]
onde \(\overline{\nu}_{\rm e}\chi_{\rm e}\) é a constante que corrige o resultado harmônico, denominada, constante de anarmonicidade.
Nota: Para se chegar ao termo adicional da equação \(\eqref{eq:MAX29}\), a função de energia potencial utilizada na equação de Schrödinger é a função de Morse [ seção 2.7 ].
No modelo vibracional harmônico \(\eqref{eq:MAX28}\), a separação entre níveis de energia consecutivos é constante, de valor:
\[\begin{equation} G _ {\nu+1} - G _ {\nu} = \overline{\nu} _ {\rm e}. \label{eq:MAX30} \end{equation}\]
Entretanto, no modelo vibracional anarmônico \(\eqref{eq:MAX29}\), a separação entre níveis de energia consecutivos não é constante, seu valor diminui, quando o número quântico vibracional aumenta:
\[\begin{equation} G _ {\nu+1} - G _ {\nu} = \overline{\nu} _ {\rm e} - 2 \, \overline{\nu} _ {\rm e} \, \chi _ {\rm e} \, (\nu + 1). \label{eq:MAX31} \end{equation}\]
O resultado \(\eqref{eq:MAX31}\) é o principal aperfeiçoamento do modelo anarmônico em relação ao harmônico. Analisando um pouco mais esse resultado, fica fácil ver que o gráfico de \(\left( G_{\nu+1} - G_{\nu} \right)\) contra \((\nu + 1)\) é uma reta que interceptação o eixo vertical em \(\overline{\nu}_{\rm e}\) e possui inclinação \((-2\overline{\nu}_{\rm e} \, \chi_{\rm e})\).
Determinado o valor da frequência espacial \(\overline{\nu}_{\rm e}\), pode-se chegar ao valor da frequêncial temporal \({\nu}_{\rm e}\), por meio do valor da velocidade da luz:
\[\begin{equation} c = \frac{{\nu} _ {\rm e}} {\overline{\nu} _ {\rm e}} \ \ \Longrightarrow \ \ {\nu} _ {\rm e} = c \, \overline{\nu} _ {\rm e}. \label{eq:MAX32} \end{equation}\]
Determinado o valor da frequêncial temporal \({\nu}_{\rm e}\), pode-se chegar ao valor da constante elástica \(k\), da suposta mola que liga os núcleos, por meio do valor da massa reduzida \(\mu\):
\[\begin{equation} \nu _ {\rm e} = \frac{1}{2\pi} \sqrt{\frac{k}{\mu}} \ \ \Longrightarrow \ \ k = \mu (2\pi \nu _ {\rm e})^2. \label{eq:MAX33} \end{equation}\]
O valor da massa reduzida é expresso em gramas (\({\rm g}\)). Ele é determinado utilizando-se as massas dos átomos que formam a molécula diatômica [ seção 2.3 ]. Mas, no “mundo dos átomos,” o grama não é utilizado como unidade padrão. A unidade padrão para a massa é a massa do isótopo 12 do carbono, dividida por 12. A esse pequenino valor, dá-se o nome de unidade de massa atômica (\({\rm u}\)), sendo:
\[\begin{equation} 1\ {\rm u}= 1,\!66 \times 10^{-24}\ {\rm g}. \label{eq:MAX33g} \end{equation}\]
Como dissemos, \(\eqref{eq:MAX31}\) lida com a separação entre níveis de energia consecutivos. De modo adicional, podemos pensar em outro espaçamento: na separação que envolve certo nível de energia \((\nu > 0)\) e o nível de energia fundamental \((\nu=0)\):
\[\begin{equation} \frac{G _ {\nu} - G _ {0}} {\nu} = \overline{\nu} _ {\rm e} - \overline{\nu} _ {\rm e} \, \chi _ {\rm e} \, (\nu + 1). \label{eq:MAX34} \end{equation}\]
O resultado \(\eqref{eq:MAX34}\) também é uma reta que intercepta o eixo vertical em \(\overline{\nu}_{\rm e}\), mas, desta vez, possui inclinação \((-\overline{\nu}_{\rm e} \, \chi_{\rm e})\).
2.6.1 O primeiro exemplo experimental
A Figura 2.6 apresenta o gráfico da equação \(\eqref{eq:MAX34}\). A Figura é construída a partir de dados experimentais da molécula diatômica de iodo, publicados por Oswaldo Sala (Sala 2008), Professor Sênior do Departamento de Química Fundamental da USP. No eixo \(x\), estão os valores \((\nu+1)\): (1+1), (2+1), (3+1), (4+1), (5+1), (6+1). Já no eixo \(y\), os dados experimentais \((G_{\nu} - G_0)/\nu\), medidos em \({\rm cm}^{-1}\): (215/1), (427/2), (638/3), (847/4), (1055/5), (1262/6).
![Gráfico da equação $\eqref{eq:MAX34}$ com os dados experimentais da molécula de iodo [@SataIodo].](index_files/figure-html/comR1-1.png)
Figura 2.6: Gráfico da equação \(\eqref{eq:MAX34}\) com os dados experimentais da molécula de iodo (Sala 2008).
Como se vê, os resultados da regressão linear estão impressos na Figura 2.6:
\[\begin{align} \overline{\nu} _ {\rm e} &= 216\ {\rm cm}^{-1}, \label{eq:MAX35}\\ \overline{\nu} _ {\rm e} \chi _ {\rm e} &= 0,\!85\ {\rm cm}^{-1}. \label{eq:MAX36} \end{align}\]
Por meio de \(\eqref{eq:MAX32}\), o resultado \(\eqref{eq:MAX35}\) implica em \(\nu_{\rm e}= 648 \times 10^{10}\ {\rm Hz}\).
A massa reduzida da molécula diatômica de iodo é: \(\mu_{\rm iodo}=M_{\rm iodo}/2\). Na tabela periódica dos elementos, encontramos \(M_{\rm iodo}=126,\!904\ {\rm u}\). Usando a conversão \(\eqref{eq:MAX33g}\), \(M_{\rm iodo}= 2,\!11 \times 10^{-22}\ {\rm g}\), o que implica em:
\[\begin{equation} \mu _ {\rm iodo} = 1,\!05 \times 10^{-22}\ {\rm g}. \label{eq:MAX38a} \end{equation}\]
Então, segundo \(\eqref{eq:MAX33}\), o valor da constante elástica idealizada para ligar os núcleos de iodo é:
\[\begin{equation} k _ {\rm iodo} = 1,\!74\ {\rm N/cm}. \label{eq:MAX38} \end{equation}\]
E, através dos resultados \(\eqref{eq:MAX35}\) e \(\eqref{eq:MAX36}\), calcula-se os valores das energias vibracionais da molécula de iodo (resultados na tabela 2.2).
| Número Quântico | Modelo Harmônico \(\eqref{eq:MAX28}\) | Modelo Anarmônico \(\eqref{eq:MAX29}\) |
|---|---|---|
| \(\left({\rm cm}^{-1}\right)\) | \(\left({\rm cm}^{-1}\right)\) | |
| \(\nu=0\) | \(G_0=108\) | \(G_0=107,\!8\) |
| \(\nu=1\) | \(G_1=324\) | \(G_1=322\) |
| \(\nu=2\) | \(G_2=540\) | \(G_2=535\) |
| \(\nu=3\) | \(G_3=756\) | \(G_3=746\) |
| \(\nu=4\) | \(G_4=972\) | \(G_4=955\) |
| \(\nu=5\) | \(G_5=1\,188\) | \(G_5=1\,162\) |
| \(\nu=6\) | \(G_6=1\,404\) | \(G_6=1\,368\) |
QUESTÕES:
Para a transição vibracional \([G_6\to G_0]\), qual é o valor da energia prevista pelo molelo harmônico?
Para a transição vibracional \([G_6\to G_0]\), qual é o valor da energia prevista pelo molelo anarmônico?
Então, para banda \([G_6\to G_0]\), qual modelo se aproxima mais do valor experimental \(1262\ {\rm cm}^{-1}\)?
O espectro infravermelho (IR) compreende entre \(100\) até \(13000\ {\rm cm}^{-1}\). Já o espectro visível (VIS) fica entre \(13000\) até \(25000\ {\rm cm}^{-1}\). Então, as transições vibracionais da molécula de iodo (tabela acima) estão no IR ou no VIS?
2.7 A função de Morse
A energia potencial rústica [ seção 2.2 ] considera os efeitos da repulsão e atração em uma molécula diatômica, mas não trás parâmetros físicos. Uma expressão mais realista foi proposta por Philip M. Morse (Morse 1929):
\[\begin{equation} V(R) = V(R_e) + D \left[1- {\rm e}^{\large -\beta(R-R_e)} \right]^2. \label{eq:MAX39} \end{equation}\]
Considerando o exemplo da molécula de iodo [ seção 2.6.1 ], e ajustando \(V(R_e)=0\), o perfil da função de Morse é apresentado na Figura 2.7.
![Função de Morse para a molécula de iodo do [ exemplo \@ref(ExpIodo) ].](index_files/figure-html/comR2-1.png)
Figura 2.7: Função de Morse para a molécula de iodo do [ exemplo 2.6.1 ].
Na Figura 2.7, a linha tracejada representa a energia de dissociação molecular \(D\), sendo:
\[\begin{equation} D = \frac{\overline{\nu} _ {\rm e}}{4} \left( \frac{\overline{\nu} _ {\rm e}}{\overline{\nu} _ {\rm e}\, \chi _ {\rm e}} \right). \label{eq:MAX40} \end{equation}\]
Através do valor determinado por \(\eqref{eq:MAX40}\), chega-se ao valor do parâmetro \(\beta\):
\[\begin{equation} \beta = \sqrt{ \frac{k}{2hcD}}. \label{eq:MAX41} \end{equation}\]
Com os dados da molécula de iodo, e lembrando que \(hc = 1,\!9865 \times 10^{-25}\ {\rm Jm}\):
\[\begin{align} D _ {\rm iodo} &= 13\,722\ {\rm cm}^{-1}, \label{eq:MAX42}\\ \beta _ {\rm iodo} &= 1,\!79\ \unicode{xC5}^{-1}. \label{eq:MAX43} \end{align}\]
Quando o número quântico vibracional se torna elevado, o nível de energia vibracional se aproxima do topo da curva de Morse, ou seja, \(G_\nu \to D\). Nesse caso, as vibrações se tornam muito intensas: na Figura 2.7, a vibração internuclear chega ao redor de \(8\ \unicode{xC5}\), todavia, a distância de equilíbrio é de \(2,\!67\ \unicode{xC5}\). Por conseguinte, a atração eletrônica não é capaz de manter os núcleos coesos, levando à dissociação molecular.
UMA QUESTÃO: Quando \(G_\nu \to D_{\rm iodo}\), qual é o valor de \(\nu\)? Usar \(G_\nu\) do molelo anarmônico [ seção 2.6 ].
Respostas: \(\nu=127\).
2.8 É energia? É nível de energia?
A distinção entre as grandezas energia vibracional e nível de energia vibracional, só é percebida, quando a função de energia potencial não “sai” do zero, em outras palavras, quando a energia do fundo do poço é diferente de zero. O motivo é simples! Se \(V(R_e) \ne 0\), então:
\[\begin{equation} \epsilon = V(R_e) + G. \label{eq:nivel1} \end{equation}\]
Na equação \(\eqref{eq:nivel1}\), \(\epsilon\) é a energia vibracional, \(V(R_e)\) é o fundo do poço, e \(G\) é o nível de energia vibracional:
\[\begin{equation} G _ \nu = \overline{\nu} _ {\rm e} (\nu + 0,\!5) - \overline{\nu} _ {\rm e} \chi _ {\rm e} (\nu + 0,\!5)^2. \label{eq:nevel2} \end{equation}\]

Figura 2.8: A energia vibracional e o nível de energia vibracional.
Conforme se vê na Figura 2.8, somente quando \(V(R_e)=0\), os termos energia vibracional e nível de energia vibracional podem ser intercambiados [ como feito no exemplo 2.6.1 ].
2.9 As transições vibracionais
A radiação no infravermelho (IR) pode alterar o estado vibracional de uma molécula, fazendo com que a oscilação seja mais intensa. Uma condição, é a energia do fóton incidente ser igual à energia de certa transição molecular. Por exemplo, no caso da transição ocorrer entre níveis de energia consecutivos:
\[\begin{equation} E _ {\rm fóton} = G _ {\nu+1} - G _ {\nu}. \label{eq:MAX44} \end{equation}\]
A radiação IR pode alterar a vibração molecular, mas não modifica a distribuição dos elétrons ao redor dos núcleos. Em outras palavras, as transições causadas por IR não modificam o valor da constante elástica \(k\), nem sequer alteram o valor do número de onda \(\overline{\nu}_{\rm e}\), pois \(\overline{\nu}_{\rm e}\) é função de \(k\) [ seção 2.6 ]. Diz-se, então, que as transições causadas por IR ocorrem entre níveis vibracionais pertencentes ao mesmo harmônico.
Para que os elétrons mudem sua distribuição ao redor dos núcleos, se faz necessário mais energia do que a fornecida pela radiação IR. Uma possibilidade é usar a radiação visível (VIS):
\[\begin{equation} {\rm Energia\ em\ cm^{-1}} \left\{ \begin{array}{lr} {\rm IR} & 100 \to 13\,000 \\ {\rm VIS} & 13\,000 \to 25\,000 \end{array} \right. \notag \end{equation}\]
\[\begin{equation} {\rm Energia\ em\ eV} \left\{ \begin{array}{lr} {\rm IR} & 0,\!0124 \to 1,\!63 \\ {\rm VIS} & 1,\!63 \to 3,\!10 \end{array} \right. \notag \end{equation}\]
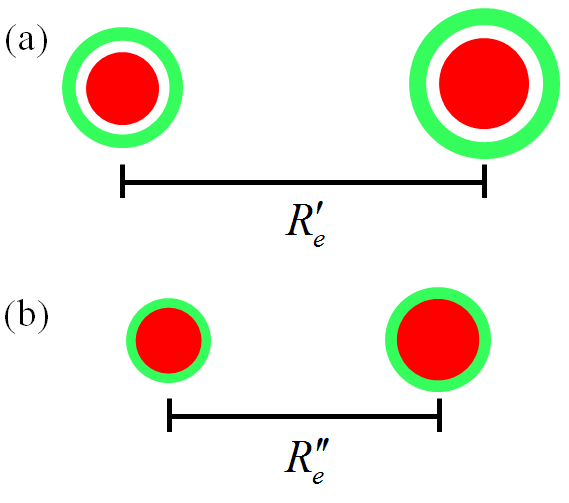
Figura 2.9: (a) Molécula no estado eletrônico excitado. (b) Molécula no estado eletrônico fundamental.
A radiação VIS pode alterar a distribuição eletrônica ao redor dos núcleos e, como consequência, também pode alterar a vibração molecular. Isso é ilustrado na Figura 2.9. Os elétrons no estado fundamental se distribuem nas proximidades dos núcleos, conforme arranjo 2.9, parte (b). Ao serem promovidos a um estado excitado, se afastam dos núcleos, conforme arranjo 2.9, parte (a). Agora, mais dispersos, os elétrons diminuem a influência de manter os núcleos coesos, pois se reduz a intensidade da força atrativa. Em outras palavras, diminui o valor da constante elástica \(k\), o que implica em aumento da distância internuclear de equilíbrio \(R_e\). Surge, então, uma nova curva de Morse [ seção 2.7 ], pois as grandezas \(\overline{\nu}_{\rm e}\), \(D\) e \(\beta\) são afetadas.
Vamos nos dequar a uma nova notação: Uma grandeza vinculada ao estado eletrônico excitado, receberá o sobrescrito \(^{´}\), como em \(R_e^{´}\). E a mesma grandeza vinculada ao estado eletrônico fundamental, receberá o sobrescrito \(^{"}\), como em \(R_e^{"}\). Nessa nomenclatura, diz-se que certa transição vibracional acontece entre 2 níveis de energia que pertencem a 2 harmônicos. A transição ocorre do harmônico \(\overline{\nu}_{\rm e}^{"}\) para o harmônico \(\overline{\nu}_{\rm e}^{´}\), ou vice-versa.
2.9.1 O segundo exemplo experimental
No modelo vibracional anarmônico [ seção 2.6 ], a separação entre níveis de energia consecutivos é determinada por:
\[\begin{equation} G _ {\nu+1} - G _ {\nu} = \overline{\nu} _ {\rm e} - 2 \, \overline{\nu} _ {\rm e} \, \chi _ {\rm e} \, (\nu + 1). \label{eq:MAX46} \end{equation}\]
A Figura 2.10 apresenta o gráfico de \(\eqref{eq:MAX46}\). Novamente recorremos aos dados experimentais da molécula diatômica de iodo (Sala 2008). No eixo \(x\), estão os valores \((\nu+1)\): (20+1), (21+1), até, (42+1). No eixo \(y\), os dados experimentais \((G_{\nu+1}^{´} - G_{\nu}^{´} )\), medidos em \({\rm cm}^{-1}\):
\[\begin{align} G _ {21}^{´} - G _ {20}^{´} &= 88, & G _ {29}^{´} - G _ {28}^{´} &= 73, & G _ {37}^{´} - G _ {36}^{´} &= 56, \notag\\ G _ {22}^{´} - G _ {21}^{´} &= 90, & G _ {30}^{´} - G _ {29}^{´} &= 72, & G _ {38}^{´} - G _ {37}^{´} &= 55, \notag\\ G _ {23}^{´} - G _ {22}^{´} &= 84, & G _ {31}^{´} - G _ {30}^{´} &= 69, & G _ {39}^{´} - G _ {38}^{´} &= 54, \notag\\ G _ {24}^{´} - G _ {23}^{´} &= 84, & G _ {32}^{´} - G _ {31}^{´} &= 67, & G _ {40}^{´} - G _ {39}^{´} &= 50, \notag\\ G _ {25}^{´} - G _ {24}^{´} &= 81, & G _ {33}^{´} - G _ {32}^{´} &= 64, & G _ {41}^{´} - G _ {40}^{´} &= 48, \notag\\ G _ {26}^{´} - G _ {25}^{´} &= 80, & G _ {34}^{´} - G _ {33}^{´} &= 64, & G _ {42}^{´} - G _ {41}^{´} &= 46, \notag\\ G _ {27}^{´} - G _ {26}^{´} &= 77, & G _ {35}^{´} - G _ {34}^{´} &= 61, & G _ {43}^{´} - G _ {42}^{´} &= 45. \notag\\ G _ {28}^{´} - G _ {27}^{´} &= 76, & G _ {36}^{´} - G _ {35}^{´} &= 57, & & \notag \end{align}\]
![Gráfico da equação $\eqref{eq:MAX46}$ com os dados experimentais da molécula de iodo [@SataIodo].](index_files/figure-html/comR3-1.png)
Figura 2.10: Gráfico da equação \(\eqref{eq:MAX46}\) com os dados experimentais da molécula de iodo (Sala 2008).
Antes de analisarmos a Figura 2.10, vamos acrescentar mais detalhes sobre a Figura 2.6.
No caso da Figura 2.6, após ser perturbada pela radiação incidente, a molécula de iodo decai para estados vibracionais que envolvem o estado eletrônico fundamental \(^{"}\). De modo que, os parâmetros vibracionais do exemplo [ 2.6.1 ] e os parâmetros da função de Morse da seção [ 2.7 ], fazem alusão a esse estado. Na nova notação, ficam assim escritos:
\[\begin{align} \overline{\nu} _ {\rm e}^{"} &= 216\ {\rm cm}^{-1}, \label{eq:MAX47}\\ \notag\\ \overline{\nu} _ {\rm e}^{"} \, \chi _ {\rm e}^{"} &= 0,\!85\ {\rm cm}^{-1}, \label{eq:MAX48}\\ \notag\\ k^{"} &= 1,\!74\ {\rm N/cm}, \label{eq:MAX49}\\ \notag\\ D^{"} &= 13722\ {\rm cm}^{-1}, \label{eq:MAX50}\\ \notag\\ \beta^{"} &= 1,\!79\ \unicode{xC5}^{-1}. \label{eq:MAX51} \end{align}\]
Agora vamos aos detalhes da Figura 2.10.
No caso da Figura 2.10, a perturbação provocada pela radiação incidente muda o estado inicial da molécula de iodo para estados vibracionais que pertencem ao estado eletrônico excitado \(^{´}\). De modo que, os valores da regressão linear impressos nessa Figura dizem respeito às grandezas:
\[\begin{align} \overline{\nu} _ {\rm e}^{´} &= 133\ {\rm cm}^{-1}, \label{eq:MAX52}\\ \notag\\ 2\overline{\nu} _ {\rm e}^{´} \, \chi _ {\rm e}^{´} &= 2,\!06\ {\rm cm}^{-1}. \label{eq:MAX53} \end{align}\]
Os resultados \(\eqref{eq:MAX52}\) e \(\eqref{eq:MAX53}\) implicam em:
\[\begin{align} \nu _ {\rm e}^{´} &= 399 \times 10^{10}\ {\rm Hz}, \label{eq:MAX54a}\\ \notag\\ \overline{\nu} _ {\rm e}^{´} \, \chi _ {\rm e}^{´} &= 1,\!03\ {\rm cm}^{-1}. \label{eq:MAX54} \end{align}\]
Já o resultado \(\eqref{eq:MAX52}\) produz o seguinte valor para a constante elástica que liga os núcleos de iodo no estado eletrônico excitado:
\[\begin{equation} k^{´} = 0,\!66\ {\rm N/cm}. \label{eq:MAX55} \end{equation}\]
Por fim, utilizando as fórmulas da seção [ 2.7 ], determina-se os parâmetros da função de Morse para o caso da molécula de iodo no estado eletrônico excitado:
\[\begin{align} D^{´} &= 4\,293\ {\rm cm}^{-1}, \label{eq:MAX56}\\ \notag\\ \beta^{´} &= 1,\!97\ \unicode{xC5}^{-1}. \label{eq:MAX57} \end{align}\]
A comparação dos resultados mostra que há relaxamento da constante elástica que liga os núcleos de iodo, de \(k^{"} = 1,\!74\ {\rm N/cm}\), para \(k^{´} = 0,\!66\ {\rm N/cm}\), quando os elétrons vão do estado fundamental \(^{"}\), para o estado excitado \(^{´}\). Isso aumenta distância internuclear de equilíbrio, que passa de \(R_e^{"}=2,\!67\ \unicode{xC5}\), para \(R_e^{´}=3,\!03\ \unicode{xC5}\), conforme ilustração na Figura 2.9. Ademais, a diminuição da energia de dissociação, de \(D^{"}=13\,722\ {\rm cm}^{-1}\), para \(D^{´}=4\,293\ {\rm cm}^{-1}\), mostra que a molécula no estado eletrônico fundamental \(^{"}\) é mais difícil de ionizar que no estado eletrônico excitado \(^{´}\). Seguindo a mesma linha de comparação, concluí-se que há diminuição da frequência de vibração molecular, de \(\overline{\nu}_{\rm e}^{"}=216\ {\rm cm}^{-1}\) \((\nu_{\rm e}^{"}=648\times 10^{10}\ {\rm Hz})\), para \(\overline{\nu}_{\rm e}^{´}=133\ {\rm cm}^{-1}\) \((\nu_{\rm e}^{´}=399\times 10^{10}\ {\rm Hz})\), quando os elétrons vão do estado fundamental \(^{"}\), para o estado excitado \(^{´}\).
A configuração eletrônica não permanece constante, por conseguinte, há um deslocamento do poço do estado eletrônico excitado: \(V^{´}(R_e^{´})\) assume um valor diferente de zero (Simon George 1989). A determinação desse novo valor pode ser feita com o auxílio da Figura 2.11. Segundo (Sala 2008), considera-se a transição \(\left[G _ {26}^{´} \to G _ 0^{"}\right]\) por se tratar da transição mais intensa do seu espectro de iodo.
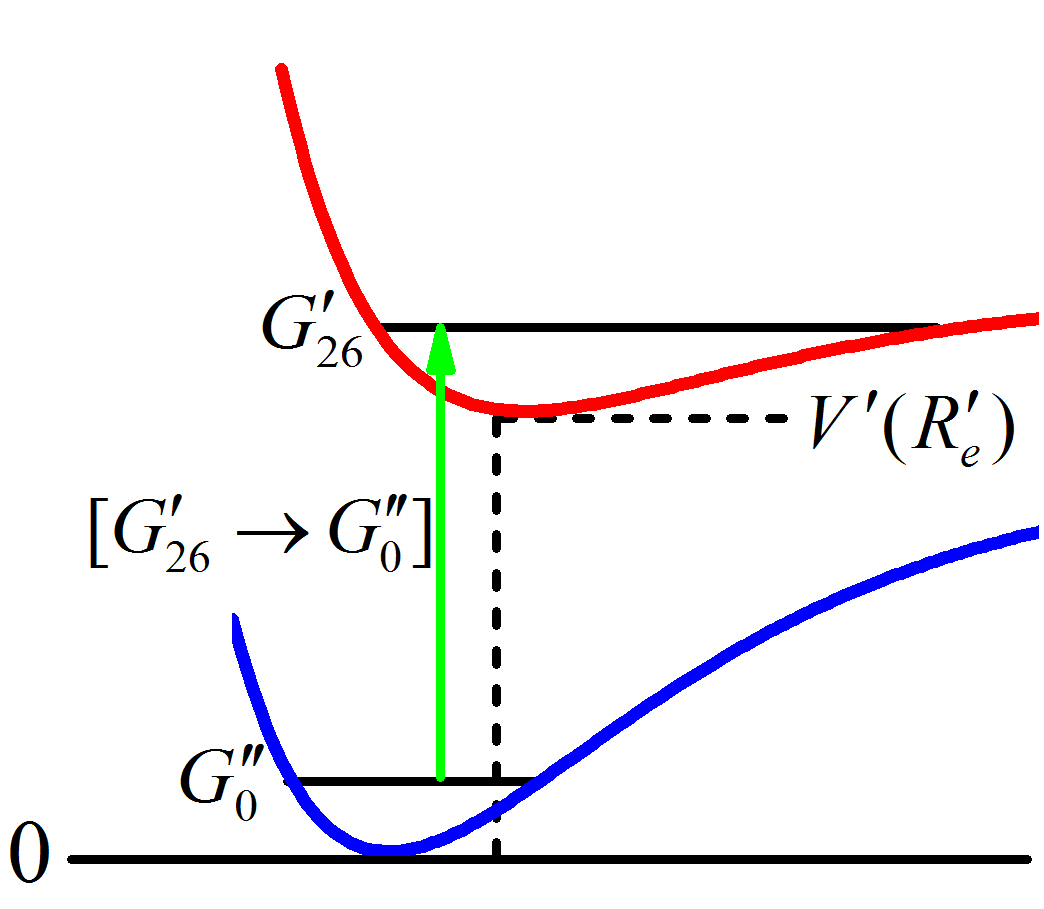
Figura 2.11: Há um deslocamento do poço do estado eletrônico excitado.
Analisando a Figura 2.11, deduz-se a expressão:
\[\begin{equation} V^{´}(R _ e^{´}) = G _ 0^{"} + \left[G _ {26}^{´} \to G _ 0^{"}\right] - G _ {26}^{´}. \label{eq:MAX58} \end{equation}\]
Com as frequências: \(\eqref{eq:MAX47}\) e \(\eqref{eq:MAX52}\), e anarmonicidades: \(\eqref{eq:MAX48}\) e \(\eqref{eq:MAX54}\), calcula-se os níveis de energia vibracional:
\[\begin{align} G _ 0^{"} &= (0+0,\!5) * 216 - (0+0,\!5)^2 * 0,\!85 = 107,\!8\ {\rm cm}^{-1}, \label{eq:MAX59}\\ \notag\\ G _ {26}^{´} &= (26+0,\!5) * 133 - (26+0,\!5)^2 * 1,\!03 = 2\,801,\!2\ {\rm cm}^{-1}. \label{eq:MAX60} \end{align}\]
Enquanto que o valor da transição \(\left[G _ {26}^{´} \to G _ 0^{"}\right]\) se encontra na Tablela 1 da referência (Sala 2008):
\[\begin{equation} \left[G _ {26}^{´} \to G _ 0^{"}\right] = 18\,403\ {\rm cm}^{-1}. \label{eq:MAX61} \end{equation}\]
Substituindo \(\eqref{eq:MAX59}\), \(\eqref{eq:MAX60}\) e \(\eqref{eq:MAX61}\) em \(\eqref{eq:MAX58}\):
\[\begin{equation} V^{´}(R _ e^{´}) = 15\,709,\!6\ {\rm cm}^{-1}. \label{eq:MAX62} \end{equation}\]
\(\blacklozenge\ \) Interpretação: A energia que desloca desloca o poço do estado eletrônico excitado, é uma energia eletrônica. Esse termo, que chamaremos de termo eletrônico \(T_{\rm e}\), engloba: a energia cinética dos elétrons, a energia de repulsão elétron-elétron, e a energia de atração elétron-núcleo.
Dito isso, a função de Morse [ seção 2.7 ] do estado eletrônico excitado é:
\[\begin{equation} V^{´}(R) = T _ {\rm e} + D^{´} \left[1- {\rm e}^{\large -\beta^{´}(R-R_e^{´})} \right]^2, \label{eq:MAX39a} \end{equation}\]
com os parâmetros \(\eqref{eq:MAX56}\), \(\eqref{eq:MAX57}\), \(R_e^{´}=3,\!03\ \unicode{xC5}\), e \(T _ {\rm e}^{´} = 15\,709,\!6\ {\rm cm}^{-1}\).
E a função de Morse do estado eletrônico fundamental é:
\[\begin{equation} V^{"}(R) = D^{"} \left[1- {\rm e}^{\large -\beta^{"}(R-R_e^{"})} \right]^2, \label{eq:MAX39b} \end{equation}\]
com os parâmetros \(\eqref{eq:MAX50}\) e \(\eqref{eq:MAX51}\), e \(R_e^{"}=2,\!67\ \unicode{xC5}\).
As curvas \(\eqref{eq:MAX39a}\) e \(\eqref{eq:MAX39b}\) são apresentadas na Figura 2.12.
![Função de Morse para o estado eletrônico fundamental e excitado da molécula de iodo [@SataIodo].](index_files/figure-html/comR4-1.png)
Figura 2.12: Função de Morse para o estado eletrônico fundamental e excitado da molécula de iodo (Sala 2008).
| Número Quântico | Estado Eletrônico Fundamental | Estado Eletrônico Excitado |
|---|---|---|
| \(\left({\rm cm}^{-1}\right)\) | \(\left({\rm cm}^{-1}\right)\) | |
| \(\nu=0\) | \(G_0^{"}=107,\!8\) | \(G_0^{´}=66,\!2\) |
| \(\nu=1\) | \(G_1^{"}=322\) | \(G_1^{´}=197\) |
| \(\nu=2\) | \(G_2^{"}=535\) | \(G_2^{´}=326\) |
| \(\nu=3\) | \(G_3^{"}=746\) | \(G_3^{´}=453\) |
| \(\nu=4\) | \(G_4^{"}=955\) | \(G_4^{´}=578\) |
| \(\nu=5\) | \(G_5^{"}=1\,162\) | \(G_5^{´}=700\) |
| \(\nu=6\) | \(G_6^{"}=1\,368\) | \(G_6^{´}=821\) |
QUESTÕES [ veja a seção 2.8 ]:
Para a molécula de iodo na estado eletrônico fundamental \(^{"}\), quais são os valores da energia vibracional \(\epsilon_{\nu}^{"}\)?
Para a molécula de iodo na estado eletrônico excitado \(^{´}\), quais são os valores da energia vibracional \(\epsilon_{\nu}^{´}\)?
3 A energia rotacional
Uma molécula diatômica, além de vibrar, também pode rodar. Em primeira aproximação, podemos modelar o movimento de rotação utilizando um rotor rígido. Usando o conceito da massa reduzida da Figura 2.4, considera-se uma partícula \(\mu\) girando em torno de uma circunferência de raio fixo \(R_e\). Durante a rotação, o momento de inércia da partícula é:
\[\begin{equation} I = \mu R_e^2. \label{eq:MAX63} \end{equation}\]
Já a magnitude de seu momento angular é:
\[\begin{equation} J = I \omega, \label{eq:MAX64} \end{equation}\]
onde \(\omega\) é a frequência angular rotacional.
A energia cinética rotacional da partícula pode ser escrita de duas maneiras. Uma em função de \(\omega\), e outra em função de \(J\):
\[\begin{equation} T = \frac{1}{2} I\omega^2 = \frac{J^2}{2I}. \label{eq:MAX65} \end{equation}\]
Visto que a rotação é em torno de de um raio fixo, pode-se impor \(V(R_e)=0\), assim, o problema não apresenta energia potencial.
O tratamento quântico do rotor rígido, consiste em resolver a equação de Schrödinger \(\hat H \Psi=E\Psi\). O operador da energia total rotacional, \(\hat H\), é construído utilizando a expressão da energia cinética \(\eqref{eq:MAX65}\). Os procedimentos matemáticos são detalhados em livros de mecânica quântica (B H Bransden 2000). Deduz-se que a energia total rotacional é quantizada, sendo a quantização uma função do número quântico rotacional \(J=0,1,2,\dots\):
\[\begin{equation} E _ J = J(J+1)B_e. \label{eq:MAX66} \end{equation}\]
Na equação \(\eqref{eq:MAX66}\), \(B_e\) é a constante rotacional em distância internuclear de equilíbrio:
\[\begin{equation} B_e = \frac{\hbar^2}{2I} \ \ \implies \ \ B_e = \frac{\hbar^2}{2 \mu R_e^2}. \label{eq:MAX67} \end{equation}\]
Utilizando o procedimento da [ seção 2.5 ], pode-se dividir \(\eqref{eq:MAX67}\) por \(hc\):
\[\begin{equation} \overline{B} _ e = \frac{h}{8\pi^2 c\, \mu R_e^2} \ \ \Longleftarrow \ \ {\rm cm^{-1}}. \label{eq:MAX68} \end{equation}\]
Daí, definindo \(F_J = \dfrac{E_J}{hc}\), a equação \(\eqref{eq:MAX66}\) fica:
\[\begin{equation} F _ J = J(J+1) \overline{B} _ e. \label{eq:MAX69} \end{equation}\]
A equação \(\eqref{eq:MAX68}\) é a fórmula para se chegar ao valor da distância internuclear de equilíbrio \(R_e\). Para isso, basta medir \((F_{J+1} - F_J)\) em uma experiência, pois, segundo \(\eqref{eq:MAX69}\), a separação entre níveis rotacionais consecutivos é:
\[\begin{equation} F _ {J+1} - F _ J = 2\overline{B} _ e (J+1). \label{eq:MAX70} \end{equation}\]
Como se vê, o gráfico de \((F_{J+1} - F_J)\) contra \((J+1)\) é uma reta que possui inclinação \(2\overline{B}_e\).
Valores experimentais de \(\overline{B} _ e\), quando os elétrons da molécula de iodo vão do estado fundamental \(^{"}\), para o estado excitado \(^{´}\), são publicados nas referências (W Kiefer 1972) e (Richard F Barrow 1973):
\[\begin{align} \overline{B} _ e ^{"} &= 0,\! 03737\ {\rm cm}^{-1}, \label{eq:MAX71}\\ \notag\\ \overline{B} _ e ^{´} &= 0,\! 02903\ {\rm cm}^{-1}. \label{eq:MAX72} \end{align}\]
Substituindo os valores acima na equação \(\eqref{eq:MAX68}\), estima-se as distâncias de equilíbrio da molécula de iodo:
\[\begin{align} R _ e^{"} &= 2,\! 67\ \unicode{xC5}, \label{eq:MAX73}\\ \notag\\ R _ e^{´} &= 3,\! 03\ \unicode{xC5}. \label{eq:MAX74} \end{align}\]
A comparação dos resultados mostra que há um aumento da distância internuclear de equilíbrio, quando os elétrons vão do estado fundamental \(^{"}\), para o estado excitado \(^{´}\), conforme ilustrado na Figura 2.9.
| Número Quântico | Estado Eletrônico Fundamental | Estado Eletrônico Excitado |
|---|---|---|
| \(\left({\rm cm}^{-1}\right)\) | \(\left({\rm cm}^{-1}\right)\) | |
| \(J=0\) | \(F_0^{"}=0\) | \(F_0^{´}=0\) |
| \(J=1\) | \(F_1^{"}=0,\! 0747\) | \(F_1^{´}=0,\! 0581\) |
| \(J=2\) | \(F_2^{"}=0,\! 2242\) | \(F_2^{´}=0,\! 1742\) |
| \(J=3\) | \(F_3^{"}=0,\! 4484\) | \(F_3^{´}=0,\! 3484\) |
| \(J=4\) | \(F_4^{"}=0,\! 7474\) | \(F_4^{´}=0,\! 5806\) |
| \(J=5\) | \(F_5^{"}=1,\! 1211\) | \(F_5^{´}=0,\! 8709\) |
| \(J=6\) | \(F_6^{"}=1,\! 5696\) | \(F_6^{´}=1,\! 2193\) |
UMA QUESTÃO: Por meio de \(\eqref{eq:MAX70}\), determina-se a separação entre níveis rotacionais consecutivos: \(2\overline{B}_e\), \(4\overline{B}_e\), \(6\overline{B}_e\), e assim por diante. Então, conforme \(\eqref{eq:MAX71}\) e \(\eqref{eq:MAX72}\), as transições rotacionais da molécula de iodo se localizam em qual faixa do espectro eletromagnético?
\[\begin{equation} {\rm Energia\ em\ cm^{-1}} \left\{ \begin{array}{lrll} {\rm Microondas} &0,\!1 &\to &100 \\ {\rm Infravermelho} &100 &\to &13\,000 \\ {\rm Visível} &13\,000 &\to &25\,000 \end{array} \right. \notag \end{equation}\]
4 A energia de excitação adiabática
O texto predominantemente analisa os termos vibracional e rotacional da energia molecular, porém, nesta seção, serão analisados outros termos, até se chegar à definição precisa da energia de excitação adiabática.
Por estratégia teórica, agora os núcleos vão “deixar de vibrar e girar.”
Os núcleos serão considerados fixos, de modo que, a energia cinética total nuclear será nula. Como resultado, a energia total do problema eletrônico, \(\rm E_{T}\), será a soma da energia cinética total dos elétrons, \(\rm E_{C}\), com a energia potencial total, \(\rm E_{P}\):
\[\begin{equation} \rm E _ {T} = E _ {C} + E _ {P}. \label{eq:MAX501} \end{equation}\]
A energia potencial total, é a soma da energia de interação elétron-elétron, \(\rm E_{e\mbox{-}e}\), com a energia de interação núcleo-elétron, \(\rm E_{N\mbox{-}e}\), com a energia de interação núcleo-núcleo, \(\rm E_{N\mbox{-}N}\):
\[\begin{equation} \rm E _ {P} = E _ {e\mbox{-}e} + E _ {N\mbox{-}e} + E _ {N\mbox{-}N}. \label{eq:MAX502} \end{equation}\]
Os termos energéticos dependem de \(\rm R\), da distância internuclear. Por exemplo, a molécula na geometria de equilíbrio, em \(\rm R = R_e\), tem energia total \(\rm E_{T} (R_e)\). Pode-se fazer a molécula passar por um processo adiabático de estiramento (contração e expanção), alterando o valor da distância internuclear, dessa forma, os termos energéticos manifestarão novos valores.
A Figura 4.1 mostra o comportamento da energia cinética, potencial e total, referente ao problema eletrônico da molécula de iodo, quando \(\rm 2 < R < 8\ \unicode{xC5}\). O espaçamento entre os pontos é de \(0,\!2\ \unicode{xC5}\). A linha tracejada assinala a distância internuclear de equilíbrio, \(\rm R_e\). O cálculo dos valores das energias foi realizado por meio de cálculo ab initio, utilizando o software GAMESS. Considerou-se a configuração eletrônica no estado fundamental da molécula de iodo, estado assinalado por \(^{"}\). A Figura também mostra a função de Morse [ 2.7 ] ajustada aos valores da energia total do cálculo ab initio:
\[\begin{equation} \rm E _ {T} (R) = E _ {T} (R_e) + D \left[1- e^{\large -\beta(R-R_e)} \right]^2. \label{eq:MAX503} \end{equation}\]
A unidade de energia da Figura 4.1 é o Hartree, sendo \(\rm 1\ Hartree = 219\,474,\!6\ cm^{-1}\).
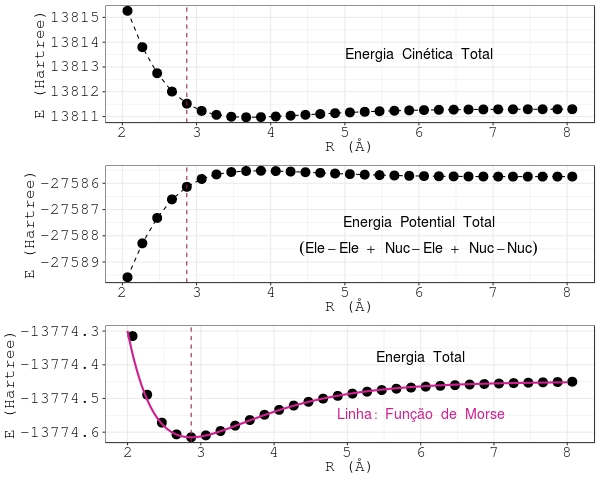
Figura 4.1: Energias cinética, potencial e total da molécula de iodo no estado eletrônico fundamental. A linha vertical assinala a distância internuclear de equilíbrio.
Os termos energéticos também podem ser agrupados de outra maneira: A energia eletrônica total, \(\rm E_{E}\), é a soma da energia cinética dos elétrons, com a energia de repulsão elétron-elétron, com a energia de atração elétron-núcleo:
\[\begin{equation} \rm E _ {E} = E _ {C} + E _ {e\mbox{-}e} + E _ {N\mbox{-}e}. \label{eq:MAX504} \end{equation}\]
De modo que, a energia total do problema eletrônico passa a ser a soma da energia eletrônica total, com a energia de repulsão núcleo-núcleo:
\[\begin{equation} \rm E _ {T} = E _ {E} + E _ {N\mbox{-}N}. \label{eq:MAX505} \end{equation}\]
A Figura 4.2 mostra o comportamento da energia eletrônica total, da energia de repulsão dos núcleos, e da energia total, para o mesmo cálculo ab initio mencionado acima. Como se vê, as Figuras 4.1 e 4.2 se completam. São duas visões da mesma energia total: uma construída pela equação \(\eqref{eq:MAX501}\), a outra, pela equação \(\eqref{eq:MAX505}\).
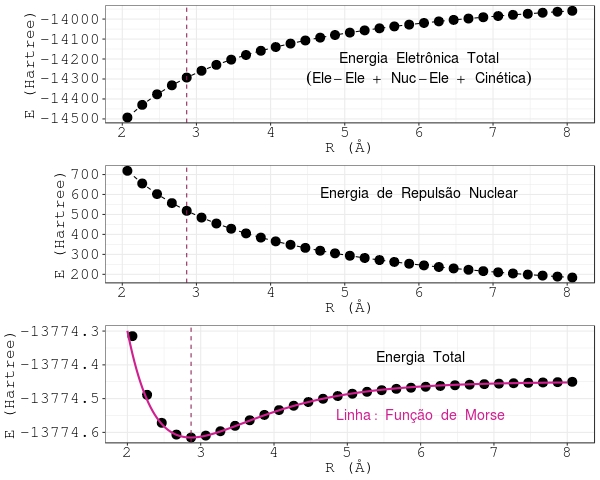
Figura 4.2: Energias eletrônica, de repulsão nuclear e total da molécula de iodo no estado eletrônico fundamental. A linha vertical assinala a distância internuclear de equilíbrio.
Alterando a configuração eletrônica para o estado excitado da molécula de iodo, estado assinalado por \(^{´}\), pode-se determinar a variação de energia entre os estados excitado \(^{´}\) e fundamental \(^{"}\): variação que chamaremos de \(\rm \Delta_{T}\) e, segundo a definição \(\eqref{eq:MAX505}\), se escreve:
\[\begin{align} \rm \Delta _ {T} &=\rm E _ {T}^{´} (R_e^{´}) - E _ {T}^{"} (R_e^{"}), \notag\\ &=\rm \left[ E _ {E}^{´} (R_e^{´}) - E _ {E}^{"} (R_e^{"}) \right] + \left[ E _ {N\mbox{-}N}^{´} (R_e^{´}) - E _ {N\mbox{-}N}^{"} (R_e^{"}) \right] , \notag\\ &=\rm \Delta _ {E} + \Delta _ {N\mbox{-}N}. \label{eq:MAX506} \end{align}\]
\(\blacklozenge\ \) Interpretação, da interpretação
Na [ seção 2.9.1 ], estando a molécula na geometria de equilíbrio, interpretou-se a variação de energia entre o estado eletrônico excitado e o fundamental, como sendo uma energia exclusivamente eletrônica. Isso está de acordo com a explicação encontrada na literatura: veja, por exemplo, a referência (McNaught 1980). Todavia, a expressão \(\eqref{eq:MAX506}\) comprova que além do termo eletrônico \(\rm \Delta_{E}\), a variação de energia entre os estados \(^{´}\) e \(^{"}\) também é composta pelo termo nuclear \(\rm \Delta_{N\mbox{-}N}\), que envolve a variação da energia de repulsão núcleo-núcleo quando a molécula passa do estado \(^{´}\) para o estado \(^{"}\).
Falta mais uma informação para harmonizar o assunto: A massa de um núcleo atômico é muito maior que a massa do elétron. Isso faz o elétron ser mais veloz que o núcleo. Então, em uma transição \(^{´}\) e \(^{"}\), os eletrons se “acomodam” rapidamente na nova configuração \(^{"}\), enquanto que os núcleos praticamente permanecem separados com a distância do estado de origem \(^{´}\), distância internuclear \(R_e^{´}\), assim, é razoálvel considerar \(\rm \Delta_{N\mbox{-}N} \to 0\), fazendo a variação de energia entre os estados \(^{´}\) e \(^{"}\) ser uma energia exclusivamente eletrônica:
\[\begin{equation} \rm \Delta _ {T} = \Delta _ {E} = E _ {E}^{´} (R _ e^{´}) - E _ {E}^{"} (R _ e^{´}) , \ \ se \ \ \Delta _ {N\mbox{-}N} \approx 0. \label{eq:MAX507} \end{equation}\]
A variação de energia \(\eqref{eq:MAX507}\) é chamada de energia de excitação adiabática, e é esta energia que é medida experimentalmente. Ademais, chama-se tal transição de transição vertical, pois o início e o fim acontece no mesmo \(\rm R\), neste caso, em \(\rm R = R_e^{´}\).
Nota 1: Na [ seção 2.9.1 ], a energia de excitação adiabática foi representada por \(T_{\rm e}\). Ademais, as energias foram transladadas de tal forma que o estado eletrônico fundamental, na geometria de equilíbrio, foi ajustado em zero, quer dizer, considerou-se \(\rm E_{T}^{"} (R_e^{"}) = 0\), conforme aparece na figura 2.12.
Nota 2: Quando foi apresentado o modelo vibracional anarmônico [ seção 2.6 ], foi dito que a função de Morse \(\eqref{eq:MAX503}\), que se ajusta à energia total \(\eqref{eq:MAX505}\), é escolhida como função de energia potencial para a determinação da energia vibracional \(G\). O motivo dessa escolha, é que a energia total do problema eletrônico, é o potencial efetivo no qual os núcleos se movem. [Ver a seção The Born-Oppenheimer approximation, na referência (Gorry 1985).]
5 Considerações finais
O artigo explorou a vibração e a rotação da molécula diatômica. Analisou-se os pormenores de três conteúdos da energia total:
A energia vibracional, que no modelo anarmônico é: \(G = \overline{\nu}_{\rm e} (\nu + 0,\!5) - \overline{\nu}_{\rm e}\chi_{\rm e}(\nu + 0,\!5)^2\);
A energia rotacional, que no modelo do rotor rígido é: \(F = J(J+1)\overline{B}_e\);
E a energia de excitação adiabática, \(T_{\rm e}\), que não apresentou expressão analítica, mas pôde ser estimada experimentalmente.
De modo que, mostrou-se que a molécula diatômica possui energia \(\, \epsilon^{´} = T_{\rm e} + G^{´} + F^{´}\), quando está no estado eletrônico excitado \(^{´}\), e energia \(\, \epsilon^{"} = G^{"} + F^{"}\), quando está no estado eletrônico fundamental \(^{"}\), sendo, \(\, \epsilon^{´} - \epsilon^{"} = T_{\rm e} + (G^{´} -G^{"}) + (F^{´} - F^{"})\), a variação de energia entre os estados excitado e fundamental.